Содержание
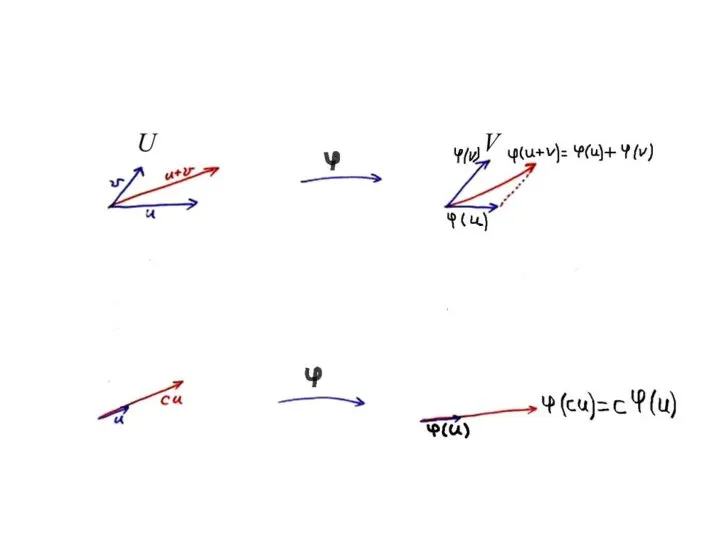
- 2. Линейное преобразование Определение 1.2 Пусть U и V - векторные пространства. Пусть u и v -
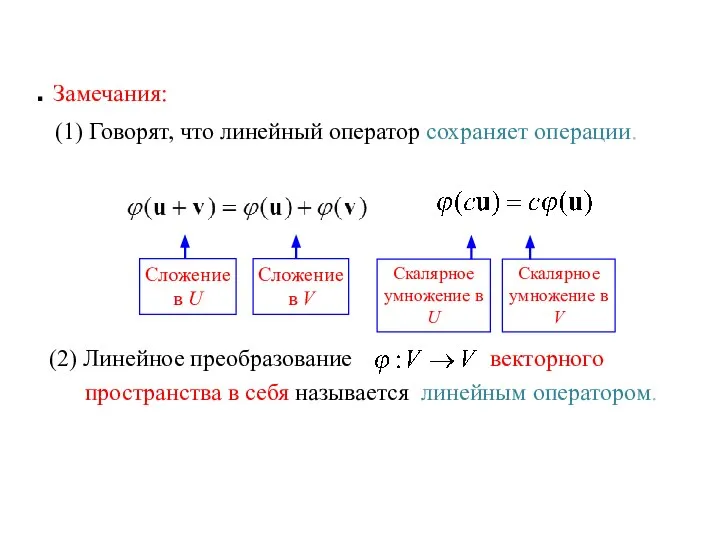
- 4. Замечания: (1) Говорят, что линейный оператор сохраняет операции. (2) Линейное преобразование векторного пространства в себя называется
- 5. Пример 1.3 Доказать, что следующее преобразование :R2 → R2 линейно. (x, y) = (x − y,
- 6. Пример 1.4 Показать, что следующее преобразование T: R3 → R2 не является линейным. (x, y, z)
- 7. Пример 1.5 Пусть Pn – векторное пространство действительных многочленов степени ≤ n. Показать, что следующее преобразование
- 8. Пример 1.6 Обозначим через D оператор дифференцирования для действительных многочленов (D есть то же самое, что
- 9. Нулевое преобразование: Единичный оператор:
- 10. Теорема 1.7: (Свойства линейного преобразования) (1) Пусть v – произвольный вектор из V. (0)= (0v) =
- 11. 2.Матричное преобразование Теорема 2.1. Пусть A есть m×n матрица. Пусть v есть элемент пространства Fn, интерпретируемый
- 12. Пример 2.2 Рассмотрим матрицу и столбец из R3. Эта матрица задает линейное преобразование (x)=Ax из R3
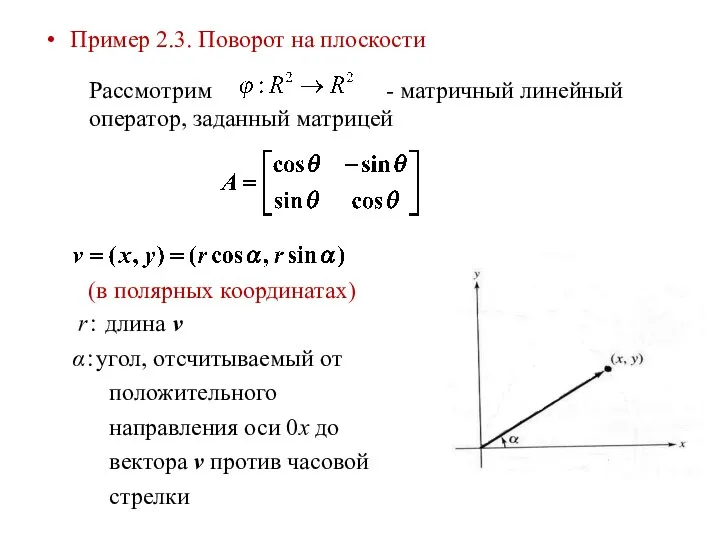
- 13. Пример 2.3. Поворот на плоскости Рассмотрим - матричный линейный оператор, заданный матрицей (в полярных координатах) r:
- 14. r:длина (v) θ +α: угол, отсчитываемый от положительного направления оси 0x до вектора (v) против часовой
- 15. 3. Матрица линейного оператора Пусть задано линейное преобразование : U→V и произвольный базис {b1 , b2
- 16. Матрица линейного оператора Пусть задан линейный оператор : V→V и произвольный базис В={b1 , b2 ,
- 17. Матрица линейного оператора Определение 3.1. Матрица Называется матрицей линейного оператора в базе В.
- 18. 4. Подобные матрицы Пусть даны два базиса В = и G = векторного пространства V и
- 19. 4. Подобные матрицы (продолжение) Получим . Определение 4.1. Две квадратные матрицы S и T одного размера
- 21. Скачать презентацию















 Пилотный проект «Прямые выплаты» с 1 января 2019 года. Часть 2
Пилотный проект «Прямые выплаты» с 1 января 2019 года. Часть 2 Реклама, стимулирование сбыта
Реклама, стимулирование сбыта Презентация на тему "Методы обучения" - скачать презентации по Педагогике
Презентация на тему "Методы обучения" - скачать презентации по Педагогике Телевидение и передача видеосигналов в ТКС
Телевидение и передача видеосигналов в ТКС Право собственности
Право собственности ИСТОКИ: СЕМЬ ЧУДЕС РОССИИ Цель урока: введение в курс предмета «Истоки» Задачи: 1. знакомство с семью выдающимися памятниками отеч
ИСТОКИ: СЕМЬ ЧУДЕС РОССИИ Цель урока: введение в курс предмета «Истоки» Задачи: 1. знакомство с семью выдающимися памятниками отеч Предмет, метод и теоретические основы методов линейного программирования
Предмет, метод и теоретические основы методов линейного программирования Изображение колеса и радиуса
Изображение колеса и радиуса  Одноэтажные промышленные здания
Одноэтажные промышленные здания History of computers
History of computers Функция - презентация по Алгебре
Функция - презентация по Алгебре «Папа Карло». Рекламное агентство
«Папа Карло». Рекламное агентство Дизайны одноэтажных домов
Дизайны одноэтажных домов Проектирование базы данных (фирма –посредник)
Проектирование базы данных (фирма –посредник) Выборки
Выборки Новообразования кожи
Новообразования кожи  Ключи к здоровью позвоночника и суставов. Тренинг
Ключи к здоровью позвоночника и суставов. Тренинг Презентация Структура предприятия
Презентация Структура предприятия ХиТРРЭ.pptx
ХиТРРЭ.pptx Использование сайтов при подготовке к ЕГЭ
Использование сайтов при подготовке к ЕГЭ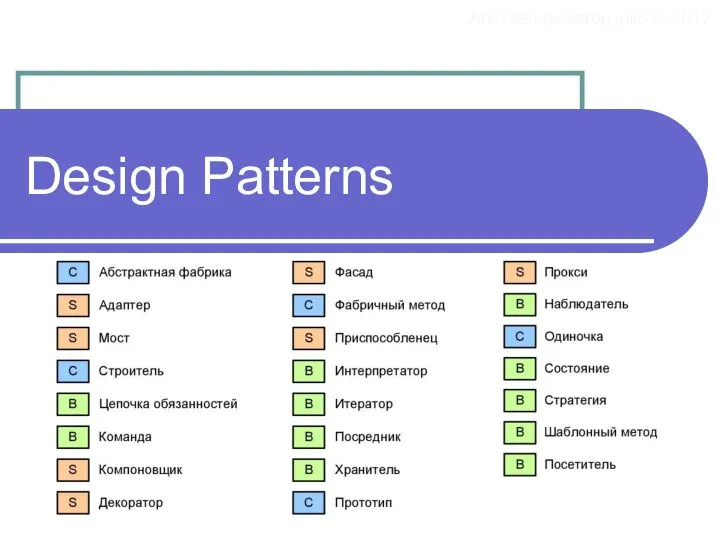 Design Patterns. Проверенные решения
Design Patterns. Проверенные решения Соленое тесто
Соленое тесто Linguistic Anthropology. Week 2
Linguistic Anthropology. Week 2 Презентация Анализ состава, структуры и динамики таможенных платежей на примере Центральной акцизной таможни
Презентация Анализ состава, структуры и динамики таможенных платежей на примере Центральной акцизной таможни Проект по биологии
Проект по биологии  Лекция 2. Основы разработки Web-приложений
Лекция 2. Основы разработки Web-приложений Методы экспертных оценок
Методы экспертных оценок Презентация "Бизнес-план" - скачать презентации по Экономике
Презентация "Бизнес-план" - скачать презентации по Экономике