Содержание
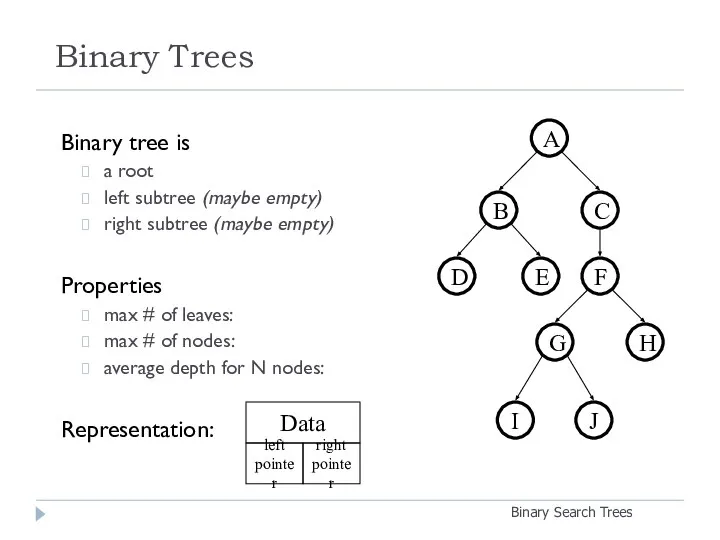
- 2. Binary Trees Binary Search Trees Binary tree is a root left subtree (maybe empty) right subtree
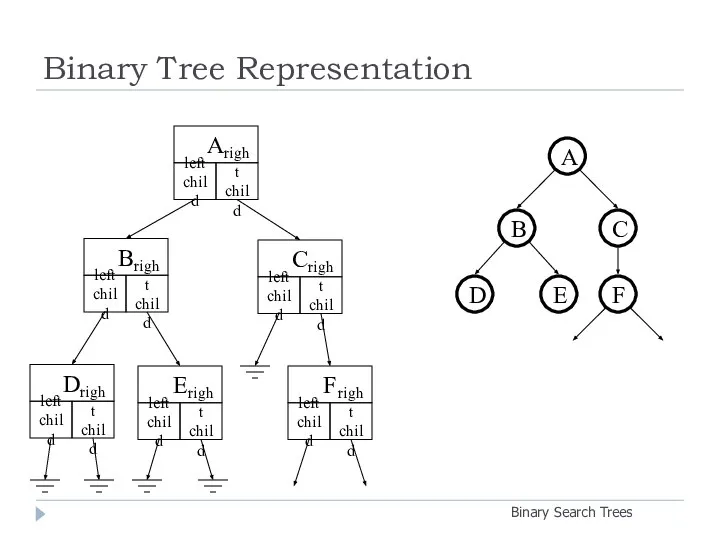
- 3. Binary Tree Representation Binary Search Trees A B D E C F
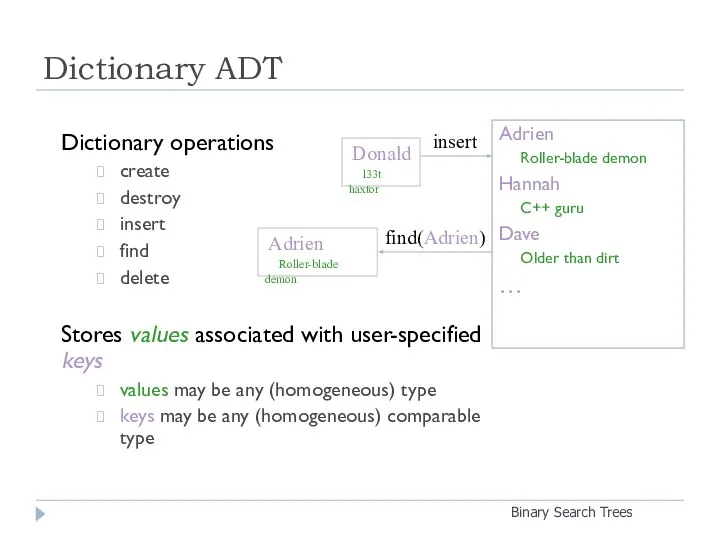
- 4. Dictionary ADT Binary Search Trees Dictionary operations create destroy insert find delete Stores values associated with
- 5. Dictionary ADT: Used Everywhere Binary Search Trees Arrays Sets Dictionaries Router tables Page tables Symbol tables
- 6. Search ADT Binary Search Trees Dictionary operations create destroy insert find delete Stores only the keys
- 7. Dictionary Data Structure: Requirements Binary Search Trees Fast insertion runtime: Fast searching runtime: Fast deletion runtime:
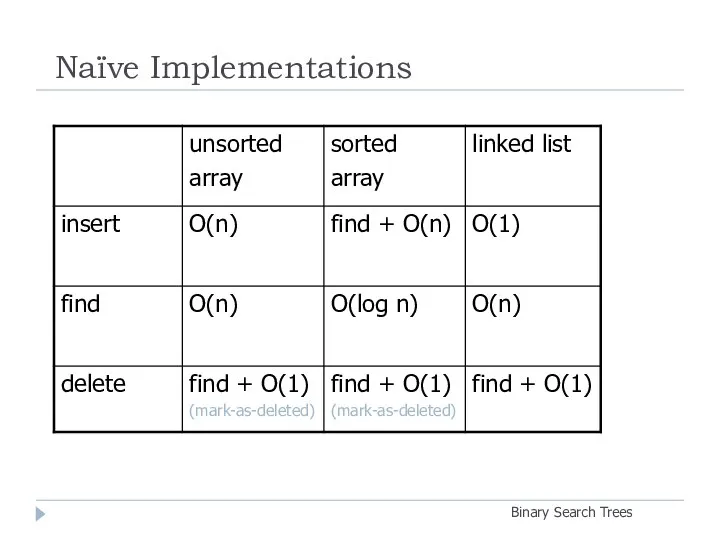
- 8. Naïve Implementations Binary Search Trees
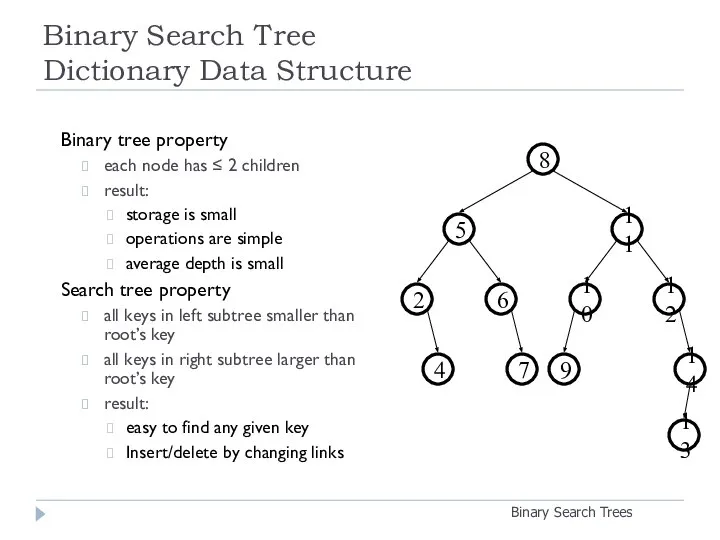
- 9. Binary Search Tree Dictionary Data Structure Binary Search Trees Binary tree property each node has ≤
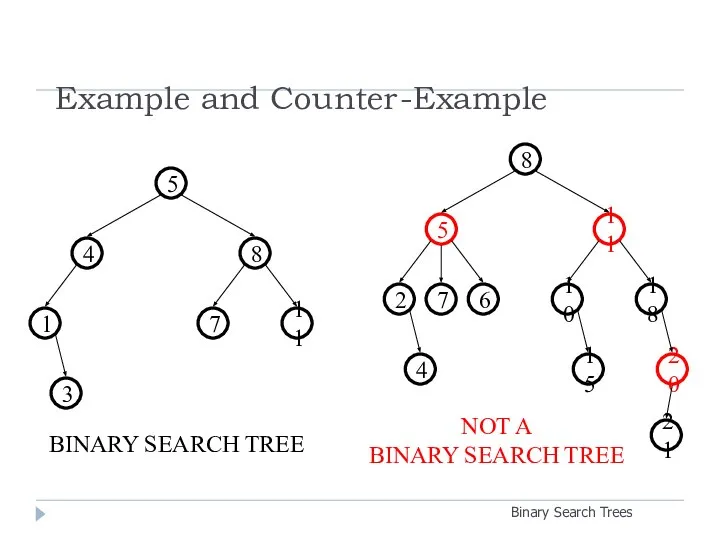
- 10. Example and Counter-Example Binary Search Trees 3 11 7 1 8 4 5 4 18 10
- 11. Complete Binary Search Tree Binary Search Trees Complete binary search tree (aka binary heap): Links are
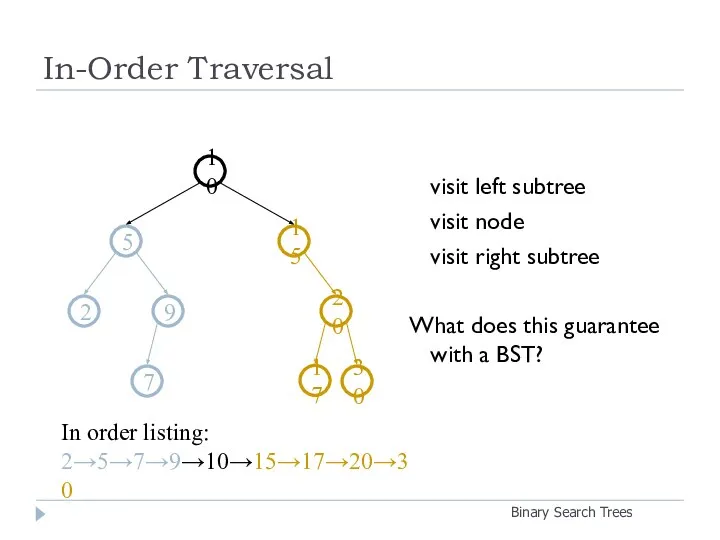
- 12. In-Order Traversal Binary Search Trees visit left subtree visit node visit right subtree What does this
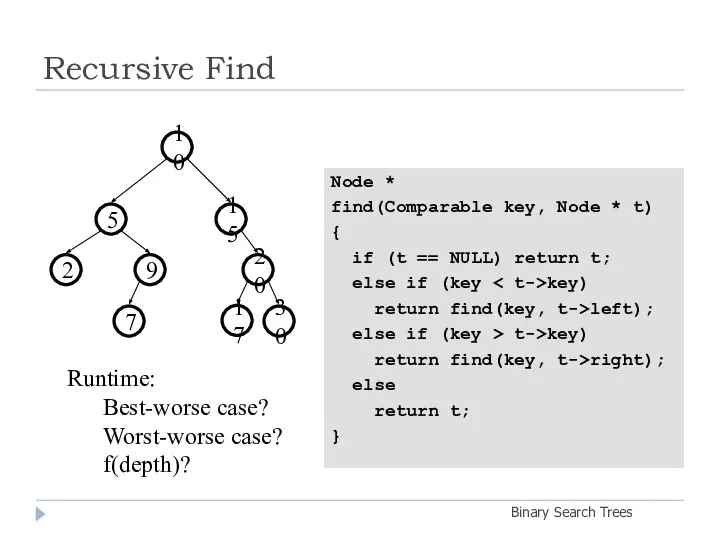
- 13. Recursive Find Binary Search Trees Node * find(Comparable key, Node * t) { if (t ==
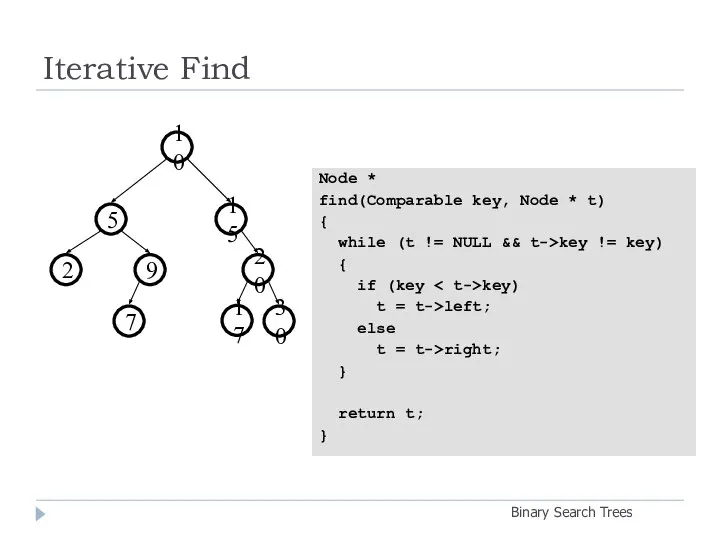
- 14. Iterative Find Binary Search Trees Node * find(Comparable key, Node * t) { while (t !=
- 15. Insert Binary Search Trees void insert(Comparable x, Node * t) { if ( t == NULL
- 16. BuildTree for BSTs Binary Search Trees Suppose the data 1, 2, 3, 4, 5, 6, 7,
- 17. Analysis of BuildTree Binary Search Trees Worst case is O(n2) 1 + 2 + 3 +
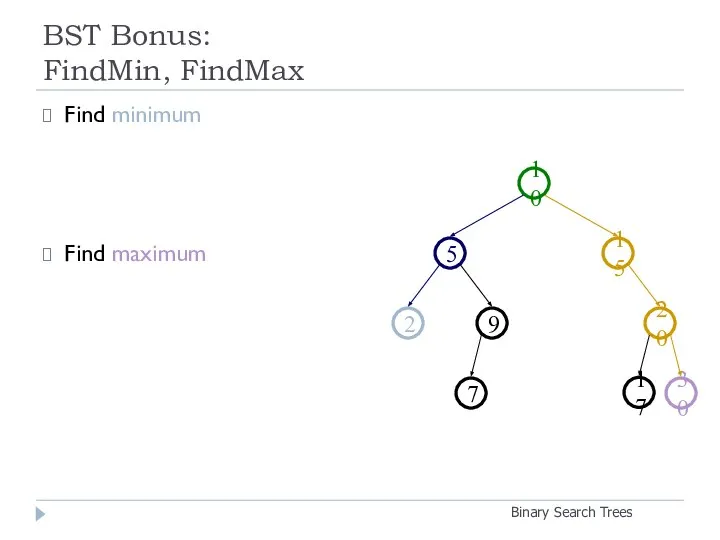
- 18. BST Bonus: FindMin, FindMax Binary Search Trees Find minimum Find maximum 20 9 2 15 5
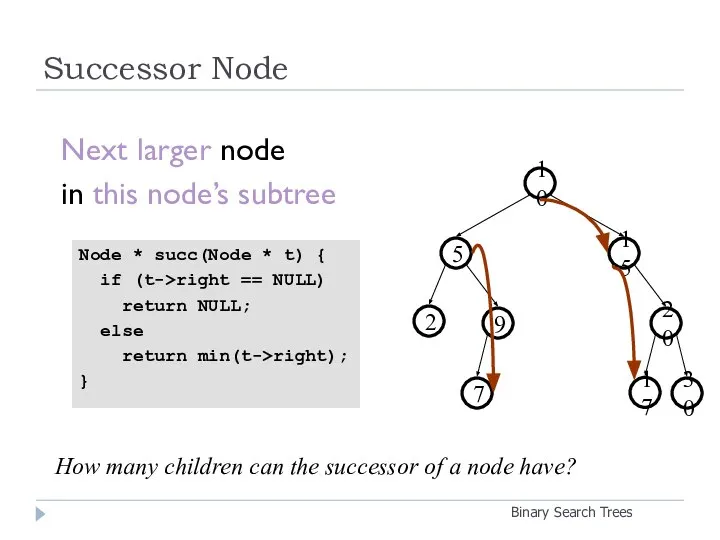
- 19. Successor Node Binary Search Trees Next larger node in this node’s subtree 20 9 2 15
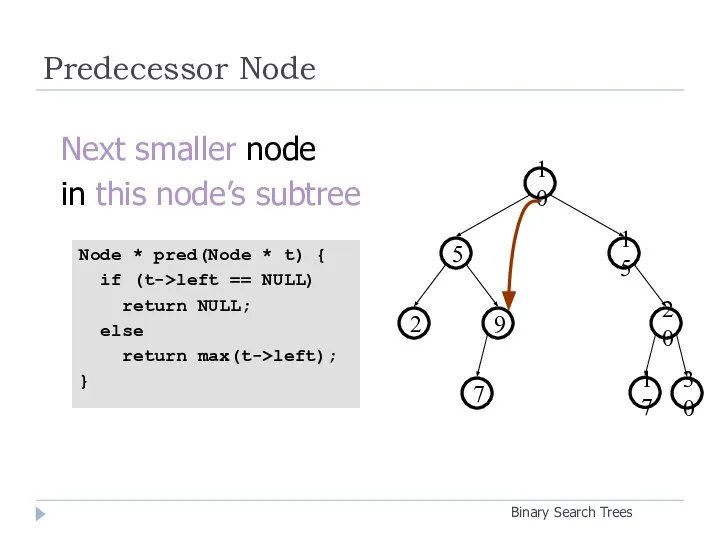
- 20. Predecessor Node Binary Search Trees 20 9 2 15 5 10 30 7 17 Next smaller
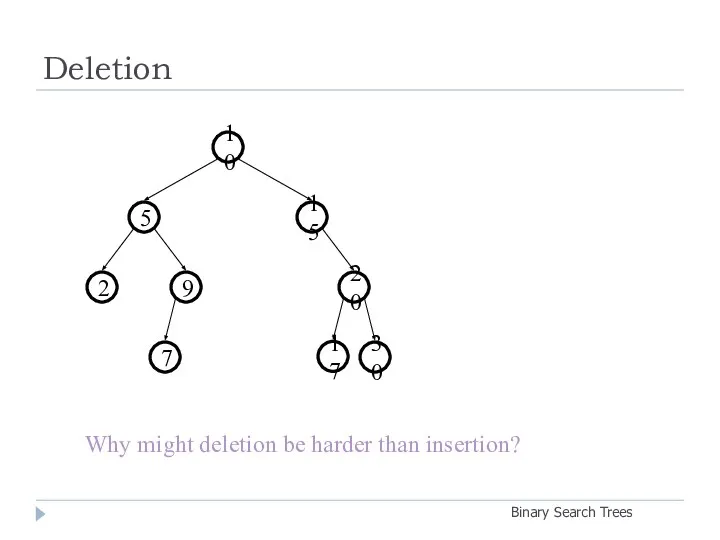
- 21. Deletion Binary Search Trees 20 9 2 15 5 10 30 7 17 Why might deletion
- 22. Lazy Deletion Binary Search Trees Instead of physically deleting nodes, just mark them as deleted simpler
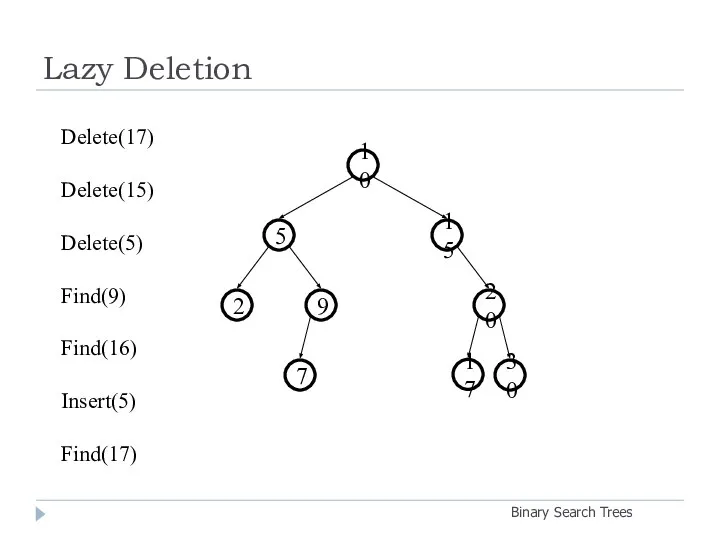
- 23. Lazy Deletion Binary Search Trees 20 9 2 15 5 10 30 7 17 Delete(17) Delete(15)
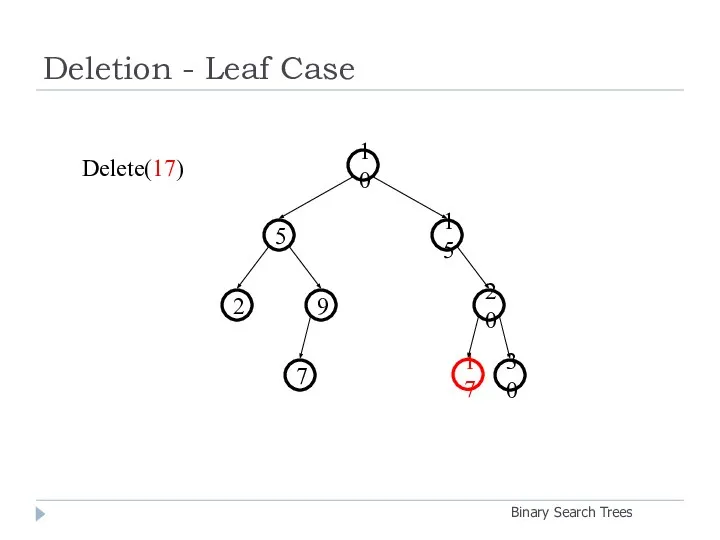
- 24. Deletion - Leaf Case Binary Search Trees 20 9 2 15 5 10 30 7 17
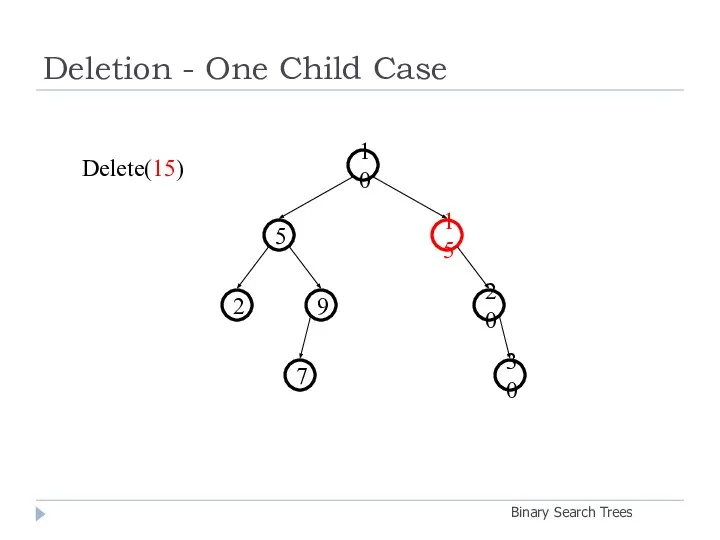
- 25. Deletion - One Child Case Binary Search Trees 20 9 2 15 5 10 30 7
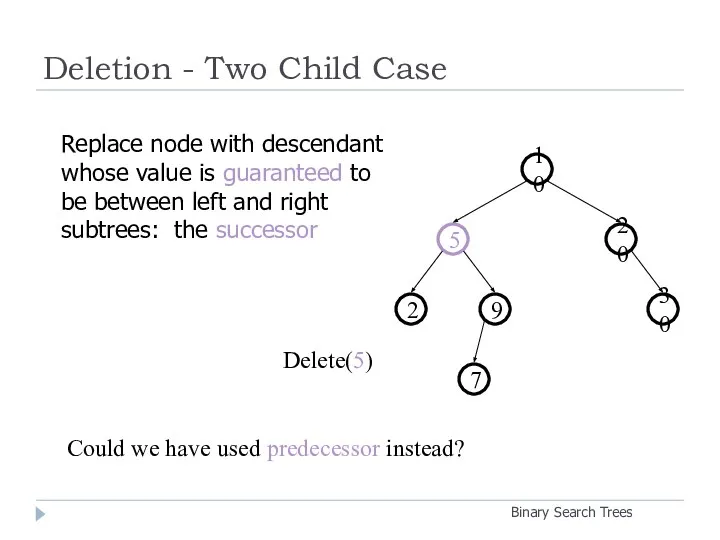
- 26. Deletion - Two Child Case Binary Search Trees 30 9 2 20 5 10 7 Delete(5)
- 27. Delete Code Binary Search Trees void delete(Comparable key, Node *& root) { Node *& handle(find(key, root));
- 28. Thinking about Binary Search Trees Binary Search Trees Observations Each operation views two new elements at
- 29. Beauty is Only Θ(log n) Deep Binary Search Trees Binary Search Trees are fast if they’re
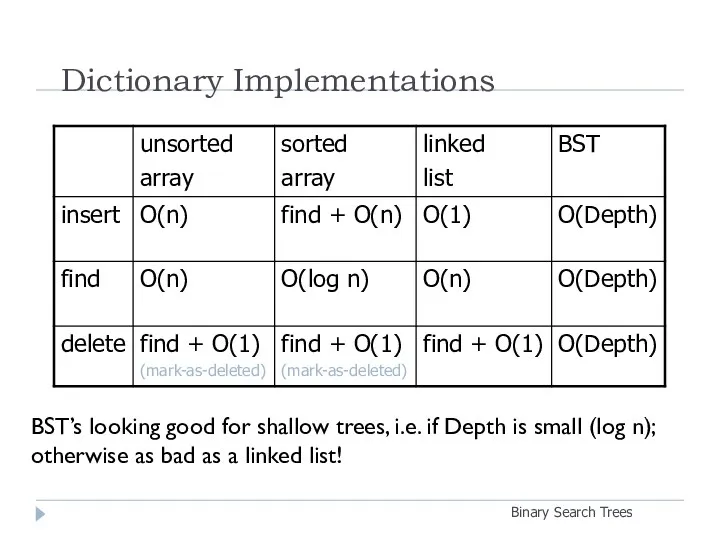
- 30. Dictionary Implementations Binary Search Trees BST’s looking good for shallow trees, i.e. if Depth is small
- 31. Digression: Tail Recursion Binary Search Trees Tail recursion: when the tail (final operation) of a function
- 33. Скачать презентацию












 Звукозапись. Носители звукозаписи
Звукозапись. Носители звукозаписи Система управления рисками
Система управления рисками  Интимный гель для женщин содержит L-аргинин способствует образованию оксида азота восстанавливает жизненно-важные функции органи
Интимный гель для женщин содержит L-аргинин способствует образованию оксида азота восстанавливает жизненно-важные функции органи Риск выбора и надежности внешнеторгового контрагента
Риск выбора и надежности внешнеторгового контрагента Документоведение и делопроизводство
Документоведение и делопроизводство Система команд МП х86
Система команд МП х86 Презентация Цена и общая стоимость контракта Виды цен Определение валюты цены
Презентация Цена и общая стоимость контракта Виды цен Определение валюты цены  Власть. Роль политики в жизни общества
Власть. Роль политики в жизни общества Особенности планирования и организации уроков рисования. Основы цветоведения. Методика ознакомления с живописью
Особенности планирования и организации уроков рисования. Основы цветоведения. Методика ознакомления с живописью Эпидемический паротит
Эпидемический паротит  Обработка ошибок
Обработка ошибок Лев Николаевич Толстой (1828 – 1910)
Лев Николаевич Толстой (1828 – 1910) Изображение и обозначение резьбы
Изображение и обозначение резьбы Эвристические комбинаторные алгоритмы
Эвристические комбинаторные алгоритмы Установка и стабилизация управляемых колес
Установка и стабилизация управляемых колес Уход за больными пожилого возраста
Уход за больными пожилого возраста География туризма
География туризма История развития физической культуры
История развития физической культуры BUENA ONDA Интернет портали за Туризъм & Резервации на хотели Здравей, Свят!
BUENA ONDA Интернет портали за Туризъм & Резервации на хотели Здравей, Свят! Универсальный спортивный комплекс «Победа»
Универсальный спортивный комплекс «Победа» История развития компьютерной техники (первое поколение ЭВМ)
История развития компьютерной техники (первое поколение ЭВМ) Модели деловой карьеры менеджера
Модели деловой карьеры менеджера Ренуар, Пьер Огюст (25 февраля 1841-2 декабря 1919)
Ренуар, Пьер Огюст (25 февраля 1841-2 декабря 1919) Имя существительное
Имя существительное Физиологические и биохимические основы физической культуры
Физиологические и биохимические основы физической культуры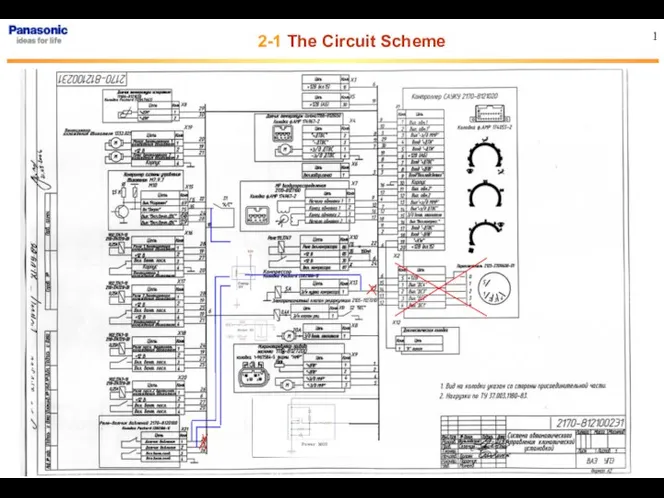 Схема климат. установки ПАНАСОНИК
Схема климат. установки ПАНАСОНИК Жиындар (массивтер
Жиындар (массивтер Travlling. sightseeings in Kazakhstan and the Uk
Travlling. sightseeings in Kazakhstan and the Uk