Содержание
- 2. 10.03.2012 10.03.2012 10.03.2012 Основная задача: Минимизировать целевую функцию Стандартная постановка задачи конечномерной оптимизации (P) на допустимом
- 3. Условия первого порядка Теорема 11.1. Пусть точка - решение задачи условной минимизации функции . Тогда не
- 4. Условия первого порядка Теорема 11.2. Пусть - точка, доставляющая минимум функции при линейных ограничениях причем первые
- 5. Функции Лагранжа Итак, как показано ранее, в точке минимума функции при ограничениях , обычно выполняется соотношение
- 6. Точная штрафная функция Флетчера В методах обычных штрафных функций решение задачи определяется как последовательность решений подзадач
- 7. Точная штрафная функция Флетчера Если представить функцию как функцию Лагранжа, в которой вектор , состоящий из
- 8. Точная штрафная функция Флетчера где - матрица, столбцами которой являются производные от вектор-функции ограничений и, следовательно,
- 9. Точная штрафная функция Флетчера Тогда Посмотрим, будет ли доставлять локальный минимум этой функции. Матрица ее вторых
- 10. Пример. Аппроксимация кривой гауссианами. где N – количество измеренных точек спектра, n - количество функций Гаусса,
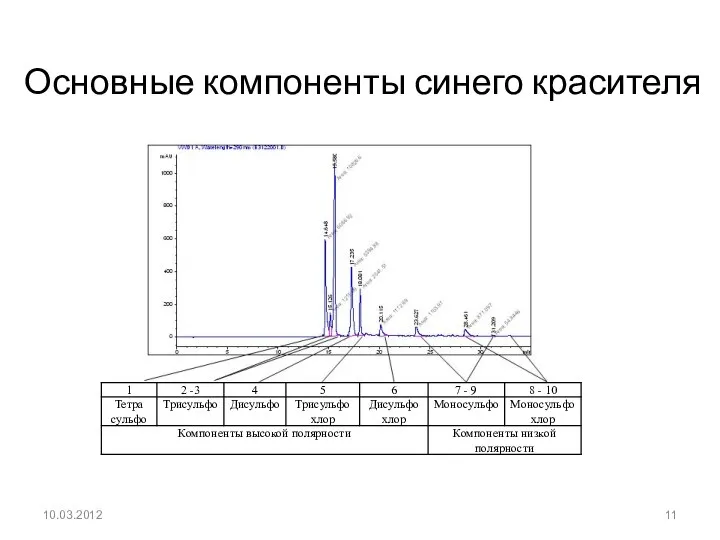
- 11. Основные компоненты синего красителя 10.03.2012
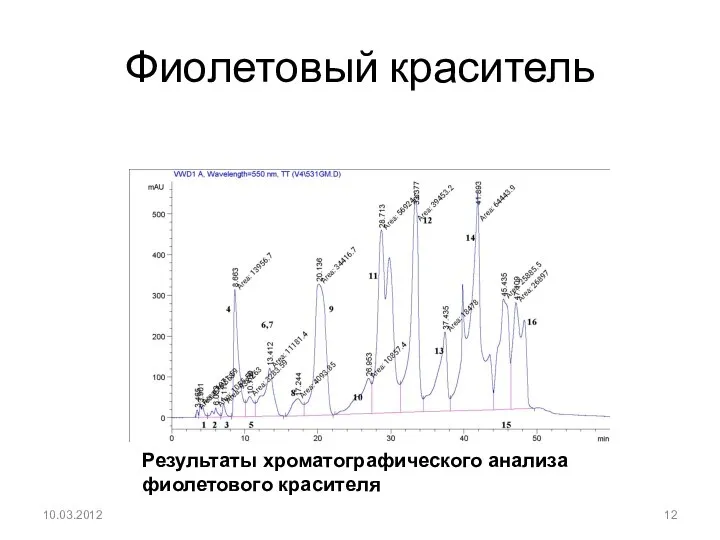
- 12. Фиолетовый краситель 10.03.2012 Результаты хроматографического анализа фиолетового красителя
- 14. Скачать презентацию









 Функции таможенных органов Работу выполнил Студент группы Т-111 Бобырь Алексей
Функции таможенных органов Работу выполнил Студент группы Т-111 Бобырь Алексей The political system of Great Britain
The political system of Great Britain Завод «Кундуз» Презентация медиа-кампании
Завод «Кундуз» Презентация медиа-кампании Готов к труду и обороне
Готов к труду и обороне Закон Вебера-Фехнера
Закон Вебера-Фехнера Suomen kielen tunnit
Suomen kielen tunnit St. Valentine’s Day
St. Valentine’s Day Олимпийское движение в Беларуси
Олимпийское движение в Беларуси Государственная кадастровая оценка земель сельскохозяйственного назначения. Методическое и технологическое обеспечение оценки
Государственная кадастровая оценка земель сельскохозяйственного назначения. Методическое и технологическое обеспечение оценки Теория Жана Пиаже
Теория Жана Пиаже Выполнение основных операций штукатурных процессов
Выполнение основных операций штукатурных процессов Современные материалы в строительстве
Современные материалы в строительстве Тайны грибного царства - презентация для начальной школы_
Тайны грибного царства - презентация для начальной школы_ Опусти свой стакан
Опусти свой стакан Герои сошли со страниц литературных произведений Презентация на тему:_
Герои сошли со страниц литературных произведений Презентация на тему:_ Форма государства Политическая система общества
Форма государства Политическая система общества Презентация "Профессия – «Экономист»" - скачать презентации по Экономике
Презентация "Профессия – «Экономист»" - скачать презентации по Экономике Стандарт OpenMP. Информационные ресурсы. Лекция 3
Стандарт OpenMP. Информационные ресурсы. Лекция 3 Презентация на тему История появления бисера
Презентация на тему История появления бисера  Internet tracking
Internet tracking Ислам
Ислам Иван Константинович Айвазовский (1817-1900)
Иван Константинович Айвазовский (1817-1900) Управление моделями в UML
Управление моделями в UML «С» - [s] [k]
«С» - [s] [k] Термодинамический потенциал в переменных S, V
Термодинамический потенциал в переменных S, V Коммерческое предложение для партнёров
Коммерческое предложение для партнёров Понятие психология Выполнила: студентка 1-ого курса ФТД группа Т-116 Цьопа Дарья
Понятие психология Выполнила: студентка 1-ого курса ФТД группа Т-116 Цьопа Дарья Maria Hoefl-Riesch. Bekannte deutsche Sportlerin
Maria Hoefl-Riesch. Bekannte deutsche Sportlerin