Содержание
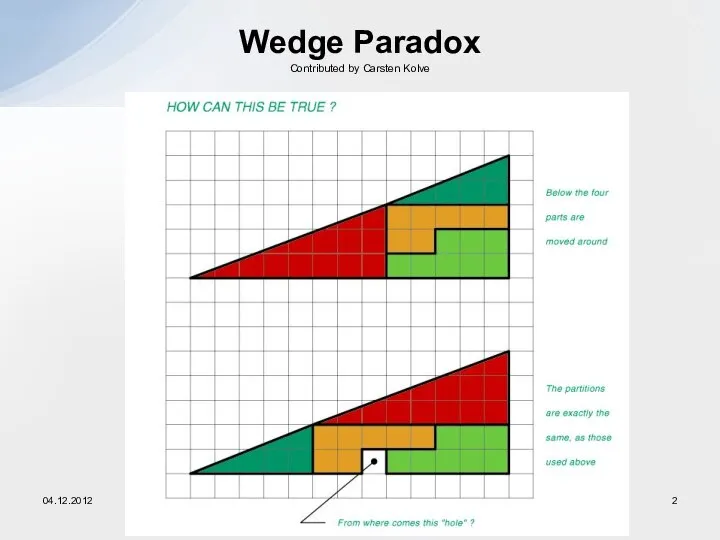
- 2. Wedge Paradox Contributed by Carsten Kolve 04.12.2012
- 3. 04.12.2012 Нанооптика Проектирование тонкопленочных структур используется в производстве: жидкокристаллических дисплеев солнечных батарей на основе диэлектриков фотоэмиссионных
- 4. 04.12.2012 Проектирование оптических покрытий состоит из следующих этапов Физическая модель Математическая модель Целевая функция – мера
- 5. 04.12.2012 Методы оптимизации Методы условной оптимизации Методы безусловной оптимизации
- 6. Что такое оптимизация? Задача оптимизации: Максимизация или минимизация некоторой функции на некотором множестве, часто представляющем собой
- 7. Что такое оптимизация? Цель изучения: Усвоение практических и теоретических аспектов: Результат моделирования: На какой результат надеяться
- 8. Свойства оптимизации как математической дисциплины Описательная – предписывающая (конструктивная) математика: Большая часть математических задач описывала ранее
- 9. Свойства оптимизации как математической дисциплины Линейные/нелинейные – выпуклые/невыпуклые: Подразделение между линейностью и нелинейностью задач гораздо менее
- 10. Свойства оптимизации как математической дисциплины Конечномерная оптимизация: Случай, когда результат расчета целевой функции соответствует выбору конечного
- 11. Конечномерная оптимизация Ограничения типа равенств и неравенств: Это условия вида (строгих неравенств стараются избегать) Интервальные ограничения:
- 12. Конечномерная оптимизация Линейные ограничения : Это условия вида (строгих неравенств стараются избегать) Параметры (данные) : Задача
- 13. Конечномерная оптимизация Параметры (данные) : Следует различать искомые переменные и коэффициенты целевой функции задачи и константы
- 14. Математическое программирование Математическое программирование – синоним конечномерной минимизации. Этот термин предшествовал термину «компьютерное программирование», который возник
- 15. - площадь поверхности коробки с банками. Пример №1. Дизайн коробки. Общее описание. При конструировании некоторых объектов,
- 16. Пример №1. Дизайн коробки. Общее ограничение. Сторона ящика не может превышать заданной величины Параметры конструкции: -
- 17. Пример №1. Дизайн коробки. Резюме. Искомыми переменными являются радиус и высота банки. Их множество допустимых значений
- 18. Пример №1. Дизайн коробки. Напомним, требуется определить радиус основания и высоту консервной банки заданного объема так,
- 19. Пример №1. Подробное рассмотрение Избыточные ограничения. Очевидно, что ограничение слабее уже имеющихся. Оно может быть без
- 20. Пример №1. Подробное рассмотрение Избыточные переменные. Конечно же, возможно разрешить уравнение и «упростить» задачу – оставить
- 22. Скачать презентацию


















 Кузьма Минин и Дмитрий Пожарский
Кузьма Минин и Дмитрий Пожарский  О мероприятиях по реализации государственной социальной политики
О мероприятиях по реализации государственной социальной политики Резьбовые соединения
Резьбовые соединения Устройство фотоаппарата
Устройство фотоаппарата Разработка проекта компании
Разработка проекта компании Тест «Эпоха Просвещения»
Тест «Эпоха Просвещения» Материаловедение. Лекция №1
Материаловедение. Лекция №1 Цель массового наблюдения
Цель массового наблюдения ВНУТРЕННИЯ И ВНЕШНЯЯ ПОЛИТИКА НИКОЛАЯ I Подготовили: Майстренко Денис Медведев Вадим Группа Т-115 ФТД
ВНУТРЕННИЯ И ВНЕШНЯЯ ПОЛИТИКА НИКОЛАЯ I Подготовили: Майстренко Денис Медведев Вадим Группа Т-115 ФТД Перемещения в стержневой системе при произвольной нагрузке. Лекция 7
Перемещения в стержневой системе при произвольной нагрузке. Лекция 7 Средневековая наука ВТОРОЙ ЭТАП РАЗВИТИЯ ПРОТОНАУКИ С V ПО XV В. Н.Э.
Средневековая наука ВТОРОЙ ЭТАП РАЗВИТИЯ ПРОТОНАУКИ С V ПО XV В. Н.Э.  Особенности деловой культуры в России
Особенности деловой культуры в России Фундаменти. Зовнішні і внутрішні стіни
Фундаменти. Зовнішні і внутрішні стіни Презентация на тему "Сурдопедагогика. Кривощёкова Н.И. Всегда говори правду (урок)" - скачать презентации по Педагогике
Презентация на тему "Сурдопедагогика. Кривощёкова Н.И. Всегда говори правду (урок)" - скачать презентации по Педагогике Методы решения квадратных уравнений - презентация по Алгебре
Методы решения квадратных уравнений - презентация по Алгебре Презентация на тему "Лечение болевых синдромов в практике терапевта" - скачать презентации по Медицине
Презентация на тему "Лечение болевых синдромов в практике терапевта" - скачать презентации по Медицине GRID история развития, технологии и стандарты (GTK, OGSA, WSRF, GPE)
GRID история развития, технологии и стандарты (GTK, OGSA, WSRF, GPE) Контроль исполнения документов
Контроль исполнения документов Функции государства
Функции государства Программирование в среде UNIX. Библиотека PCRE
Программирование в среде UNIX. Библиотека PCRE Развитие технического творчества обучающихся средствами образовательной робототехники
Развитие технического творчества обучающихся средствами образовательной робототехники Модные тенденции 2016 года
Модные тенденции 2016 года Политический конфликт
Политический конфликт Консолидированная отчетность HR/ Consolidated statement HR
Консолидированная отчетность HR/ Consolidated statement HR ДВИЖЕНИЕ ЗАРЯЖЕННЫХ ЧАСТИЦ В ГАЗЕ
ДВИЖЕНИЕ ЗАРЯЖЕННЫХ ЧАСТИЦ В ГАЗЕ  Контрабанда нефти Понятие контрабанды. Добыча нефти. Недавние факты по контрабанде нефти.
Контрабанда нефти Понятие контрабанды. Добыча нефти. Недавние факты по контрабанде нефти. Устное народное творчество (3 класс) - презентация__________________________________________________________________________________________________________________
Устное народное творчество (3 класс) - презентация__________________________________________________________________________________________________________________ Дирофиляриоз
Дирофиляриоз