- CSE 326: Data Structures. Mergeable Heaps. Lecture #22
Содержание
- 2. Summary of Heap ADT Analysis Consider a heap of N nodes Space needed: O(N) Actually, O(MaxSize)
- 3. Other Heap Operations Find and FindMax: O(N) DecreaseKey(P,Δ,H): Subtract Δ from current key value at position
- 4. But What About... Merge(H1,H2): Merge two heaps H1 and H2 of size O(N). E.g. Combine queues
- 5. Binomial Queues Binomial queues support all three priority queue operations Merge, Insert and DeleteMin in O(log
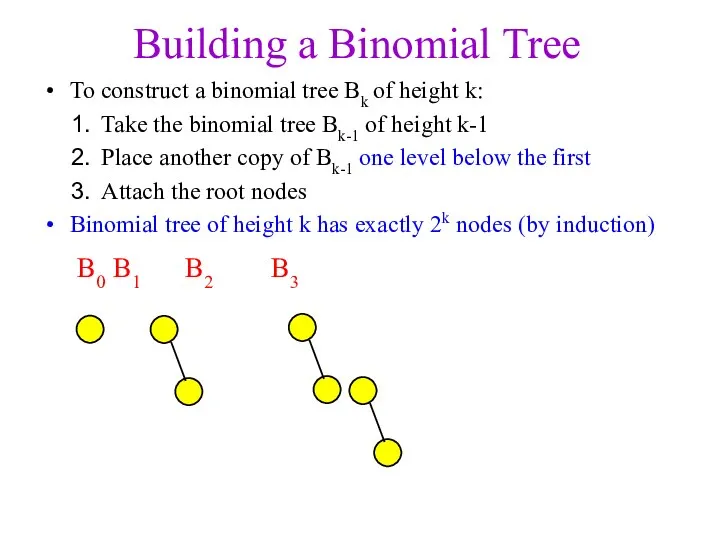
- 6. Building a Binomial Tree To construct a binomial tree Bk of height k: Take the binomial
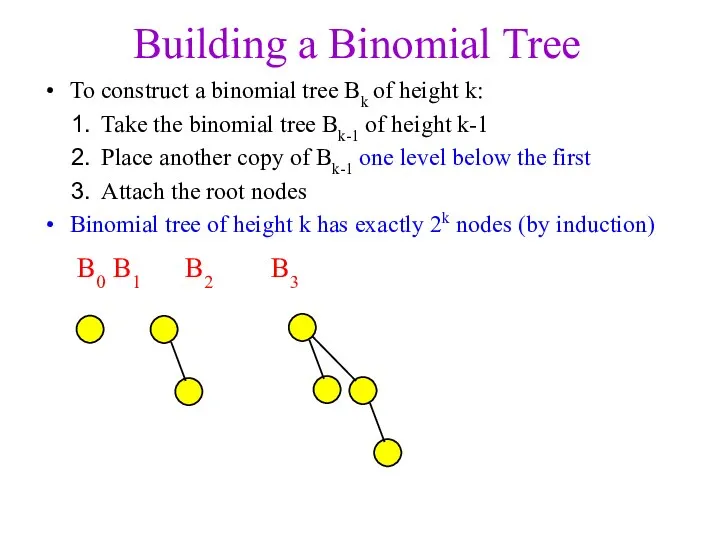
- 7. Building a Binomial Tree To construct a binomial tree Bk of height k: Take the binomial
- 8. Building a Binomial Tree To construct a binomial tree Bk of height k: Take the binomial
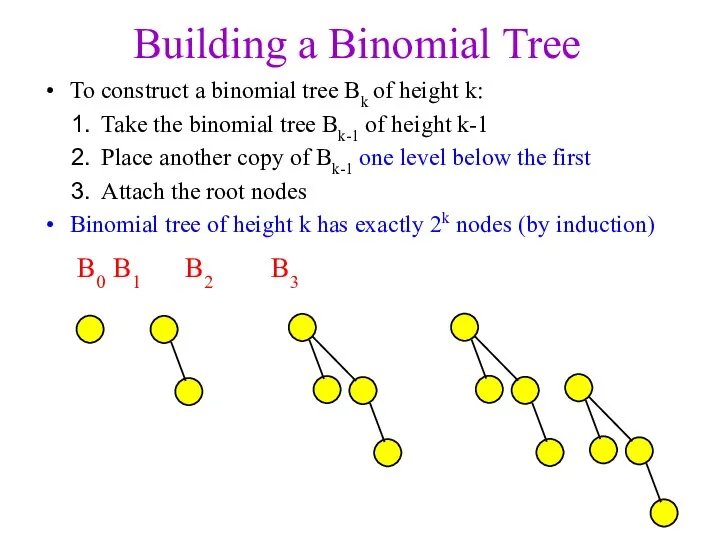
- 9. Building a Binomial Tree To construct a binomial tree Bk of height k: Take the binomial
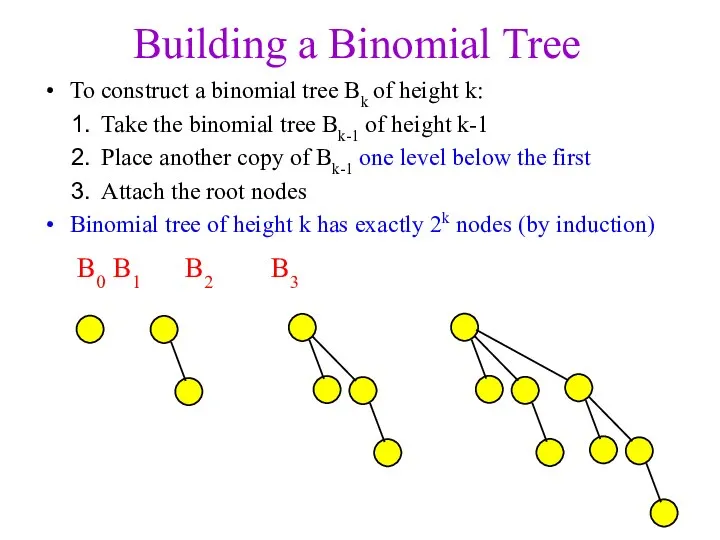
- 10. Building a Binomial Tree To construct a binomial tree Bk of height k: Take the binomial
- 11. Building a Binomial Tree To construct a binomial tree Bk of height k: Take the binomial
- 12. Building a Binomial Tree To construct a binomial tree Bk of height k: Take the binomial
- 13. Why Binomial? Why are these trees called binomial? Hint: how many nodes at depth d? B0
- 14. Why Binomial? Why are these trees called binomial? Hint: how many nodes at depth d? Number
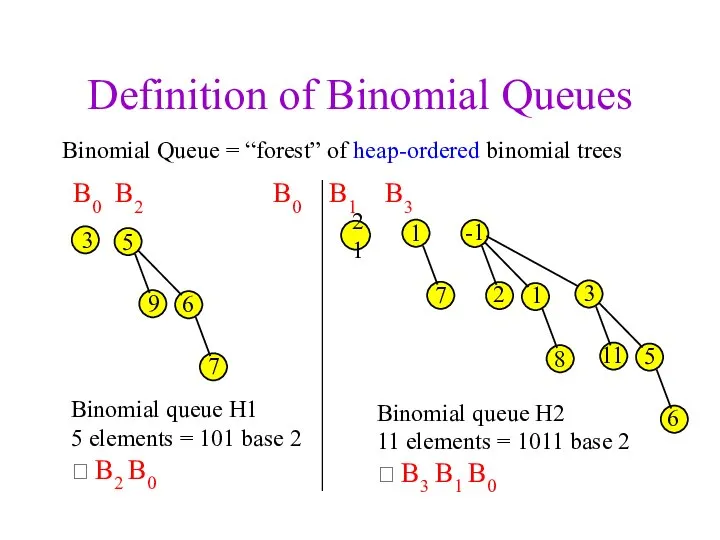
- 15. Definition of Binomial Queues 3 Binomial Queue = “forest” of heap-ordered binomial trees 1 7 -1
- 16. Binomial Queue Properties Suppose you are given a binomial queue of N nodes There is a
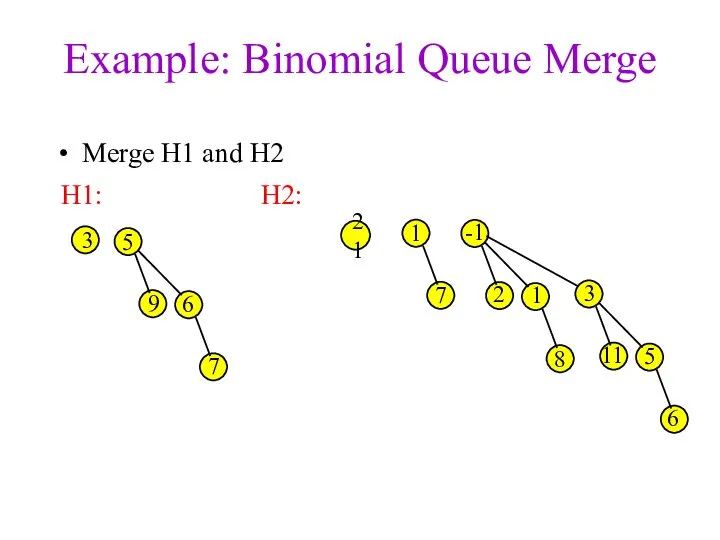
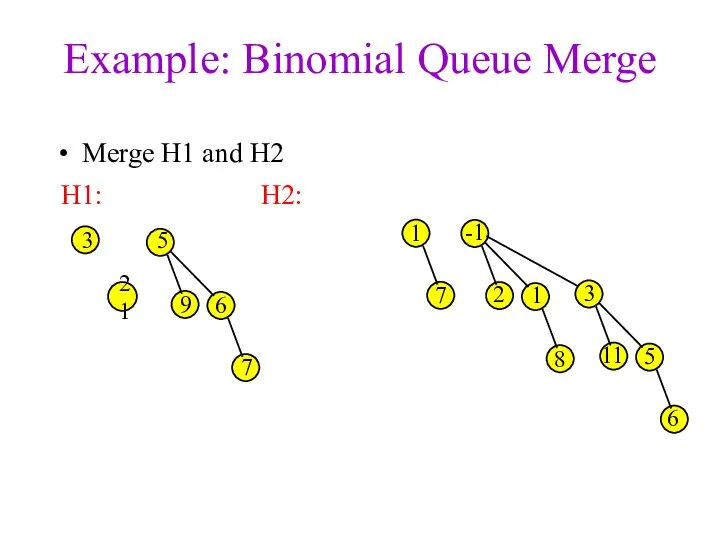
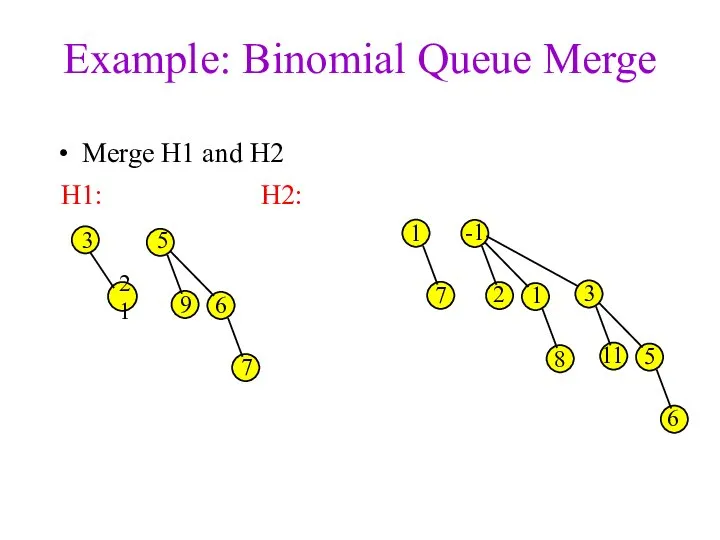
- 17. Binomial Queues: Merge Main Idea: Merge two binomial queues by merging individual binomial trees Since Bk+1
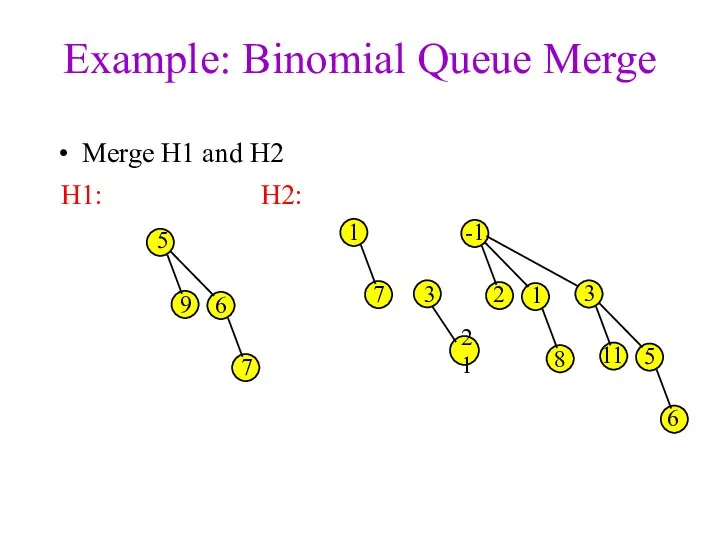
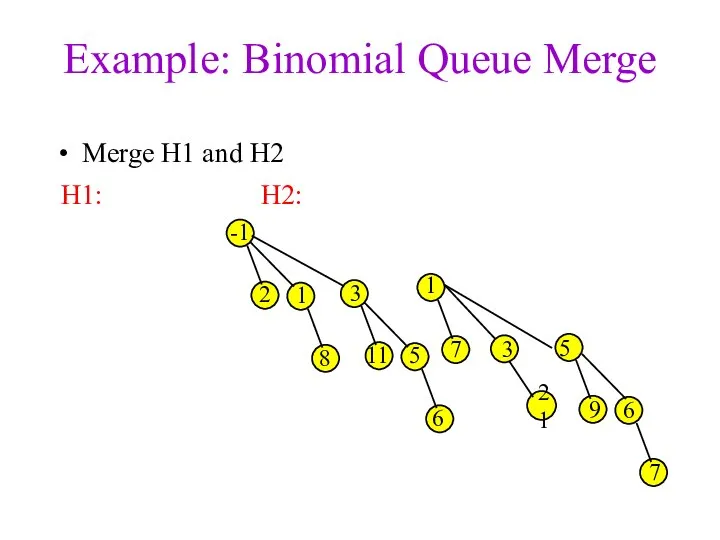
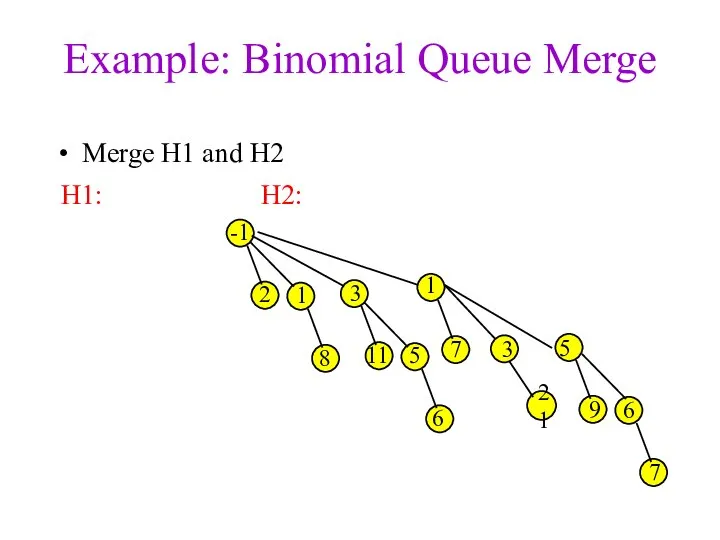
- 18. Example: Binomial Queue Merge Merge H1 and H2 3 1 7 -1 2 1 3 8
- 19. Example: Binomial Queue Merge Merge H1 and H2 3 1 7 -1 2 1 3 8
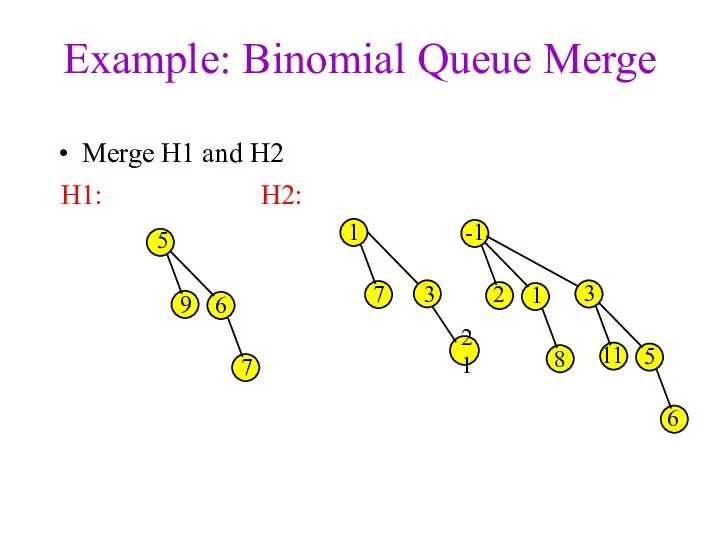
- 20. Example: Binomial Queue Merge Merge H1 and H2 3 1 7 -1 2 1 3 8
- 21. Example: Binomial Queue Merge Merge H1 and H2 3 1 7 -1 2 1 3 8
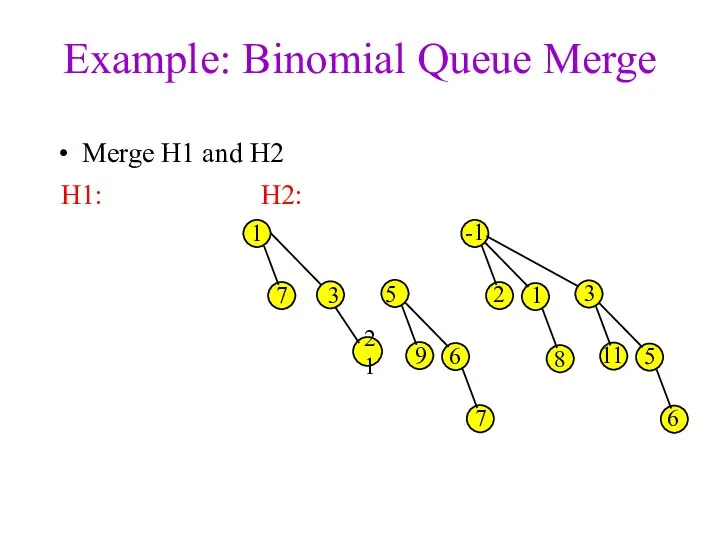
- 22. Example: Binomial Queue Merge Merge H1 and H2 3 1 7 -1 2 1 3 8
- 23. Example: Binomial Queue Merge Merge H1 and H2 3 1 7 -1 2 1 3 8
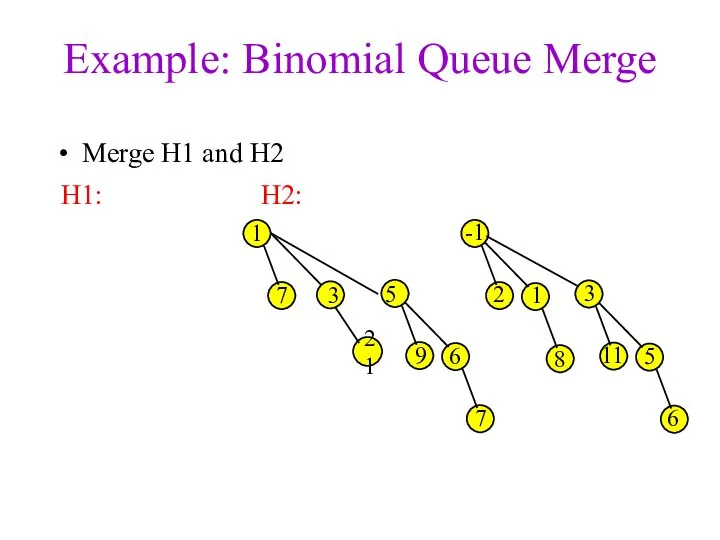
- 24. Example: Binomial Queue Merge Merge H1 and H2 3 1 7 -1 2 1 3 8
- 25. Example: Binomial Queue Merge Merge H1 and H2 3 1 7 -1 2 1 3 8
- 26. Example: Binomial Queue Merge Merge H1 and H2 3 1 7 -1 2 1 3 8
- 27. Binomial Queues: Merge and Insert What is the run time for Merge of two O(N) queues?
- 28. Binomial Queues: Merge and Insert What is the run time for Merge of two O(N) queues?
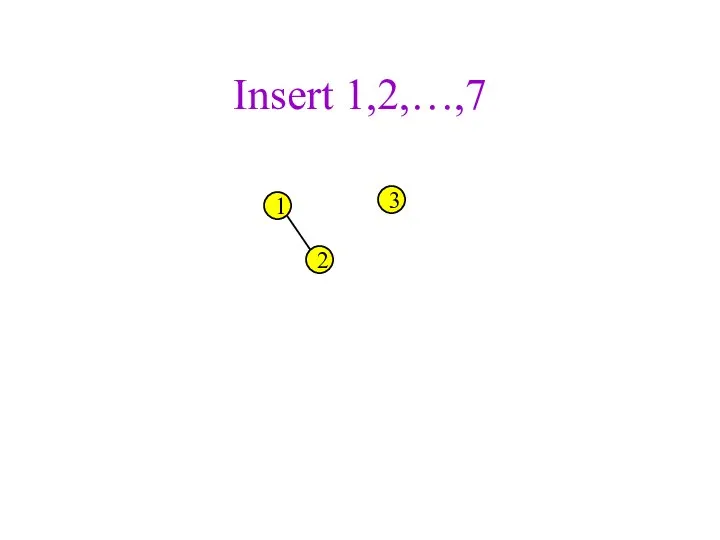
- 29. Insert 1,2,…,7 1
- 30. Insert 1,2,…,7 1 2
- 31. Insert 1,2,…,7 1 2 3
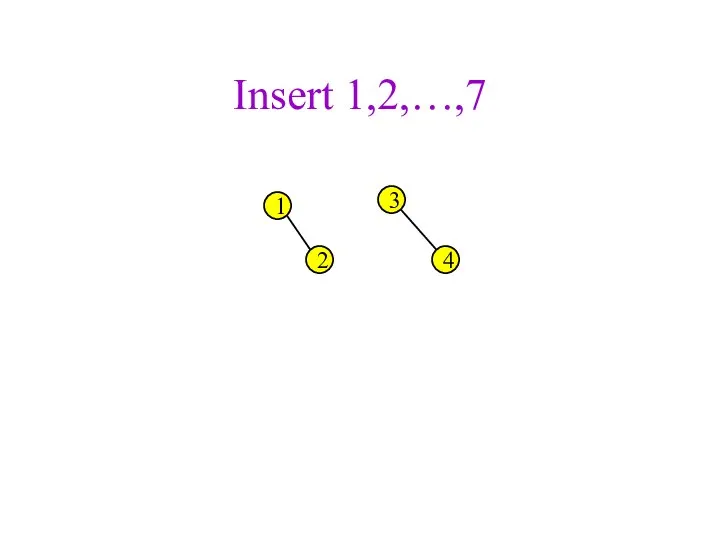
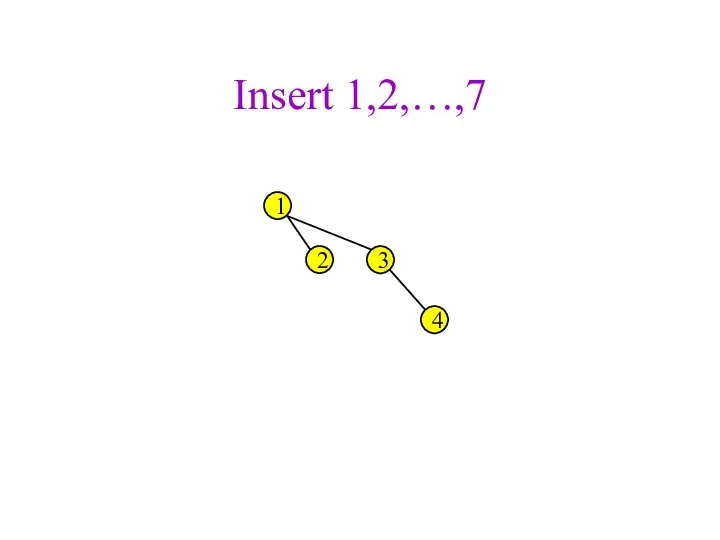
- 32. Insert 1,2,…,7 1 2 3 4
- 33. Insert 1,2,…,7 1 2 3 4
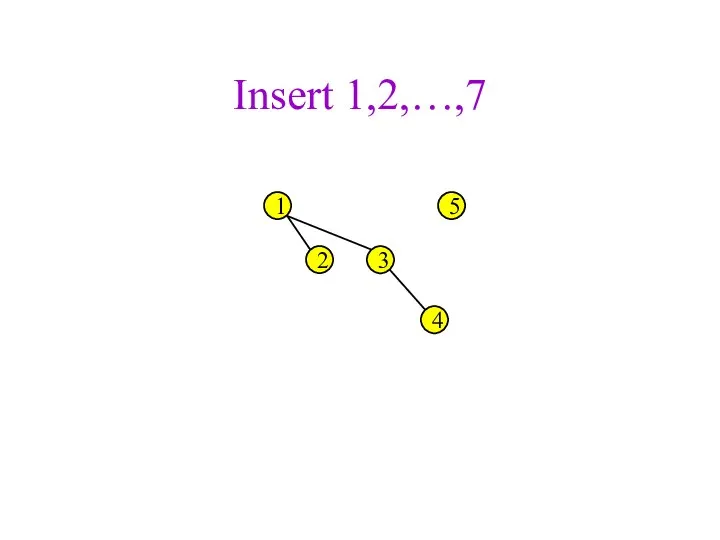
- 34. Insert 1,2,…,7 1 2 3 4 5
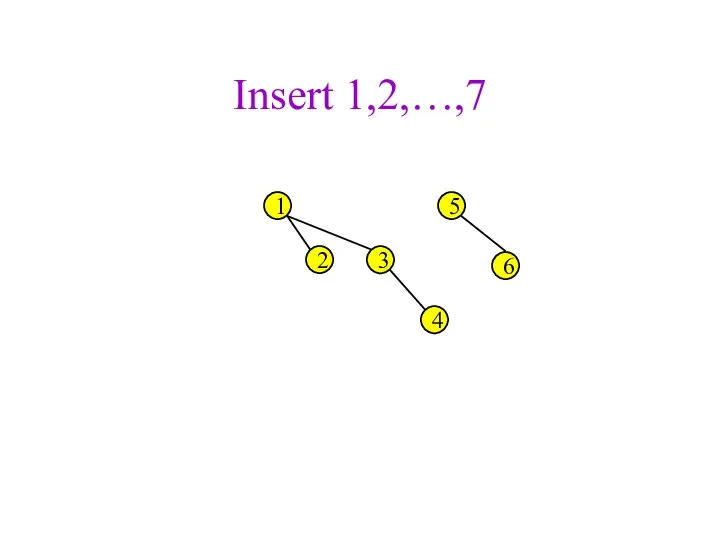
- 35. Insert 1,2,…,7 1 2 3 4 5 6
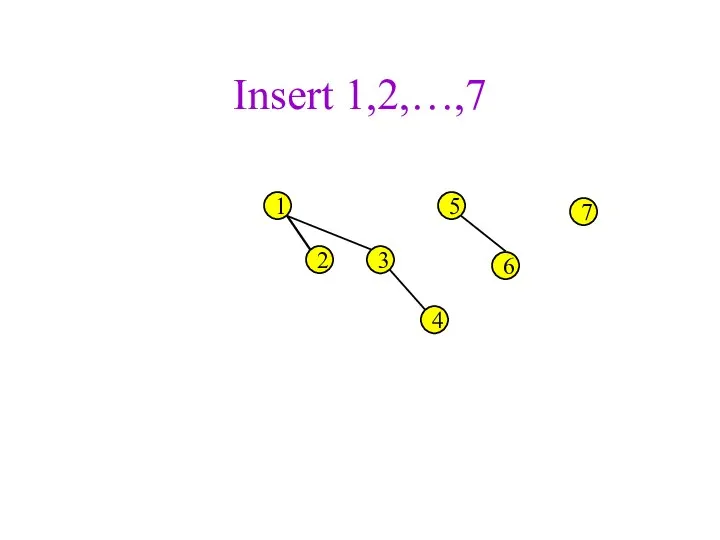
- 36. Insert 1,2,…,7 1 2 3 4 5 6 7
- 37. Binomial Queues: DeleteMin Steps: Find tree Bk with the smallest root Remove Bk from the queue
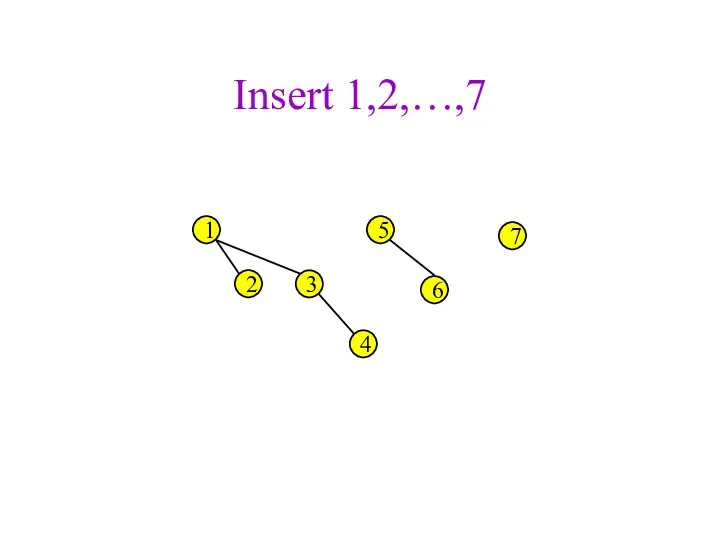
- 38. Insert 1,2,…,7 1 2 3 4 5 6 7
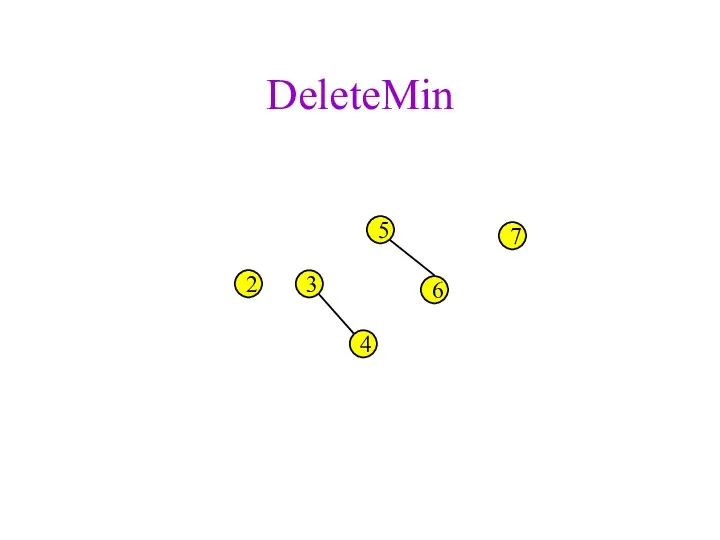
- 39. DeleteMin 2 3 4 5 6 7
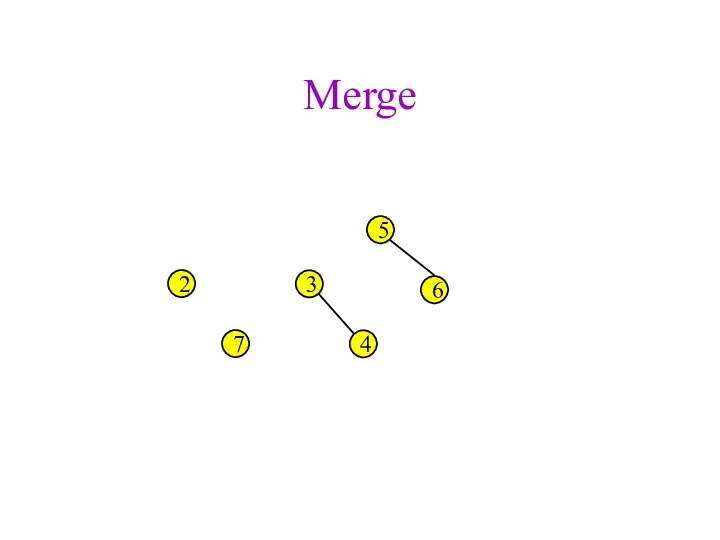
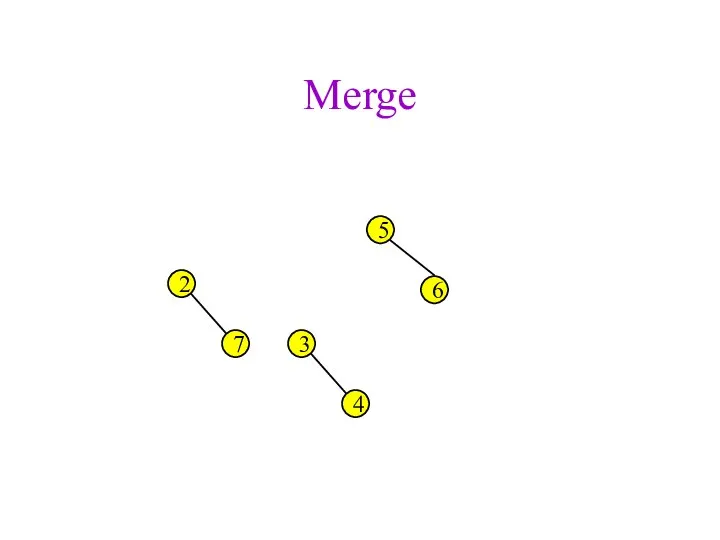
- 40. Merge 2 3 4 5 6 7
- 41. Merge 2 3 4 5 6 7
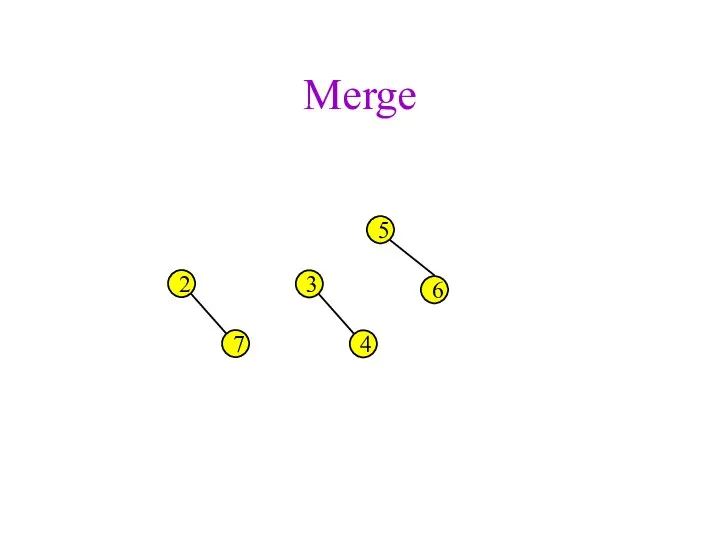
- 42. Merge 2 3 4 5 6 7
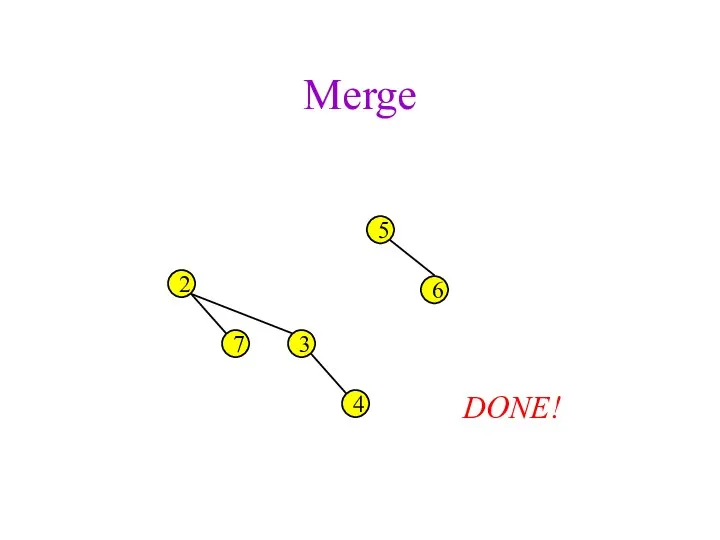
- 43. Merge 2 3 4 5 6 7 DONE!
- 44. Implementation of Binomial Queues Need to be able to scan through all trees, and given two
- 45. Other Mergeable Priority Queues: Leftist and Skew Heaps Leftist Heaps: Binary heap-ordered trees with left subtrees
- 47. Скачать презентацию
Summary of Heap ADT Analysis
Consider a heap of N nodes
Space needed:
Summary of Heap ADT Analysis
Consider a heap of N nodes
Space needed:
Other Heap Operations
Find and FindMax: O(N)
DecreaseKey(P,Δ,H): Subtract Δ from current key
Other Heap Operations
Find and FindMax: O(N)
DecreaseKey(P,Δ,H): Subtract Δ from current key
But What About...
Merge(H1,H2): Merge two heaps H1 and H2 of size
But What About...
Merge(H1,H2): Merge two heaps H1 and H2 of size
Binomial Queues
Binomial queues support all three priority queue operations Merge, Insert
Binomial Queues
Binomial queues support all three priority queue operations Merge, Insert
Building a Binomial Tree
To construct a binomial tree Bk of height
Building a Binomial Tree
To construct a binomial tree Bk of height
Building a Binomial Tree
To construct a binomial tree Bk of height
Building a Binomial Tree
To construct a binomial tree Bk of height
Building a Binomial Tree
To construct a binomial tree Bk of height
Building a Binomial Tree
To construct a binomial tree Bk of height
Building a Binomial Tree
To construct a binomial tree Bk of height
Building a Binomial Tree
To construct a binomial tree Bk of height
Building a Binomial Tree
To construct a binomial tree Bk of height
Building a Binomial Tree
To construct a binomial tree Bk of height
Building a Binomial Tree
To construct a binomial tree Bk of height
Building a Binomial Tree
To construct a binomial tree Bk of height
Building a Binomial Tree
To construct a binomial tree Bk of height
Building a Binomial Tree
To construct a binomial tree Bk of height
Why Binomial?
Why are these trees called binomial?
Hint: how many nodes at
Why Binomial?
Why are these trees called binomial?
Hint: how many nodes at
Why Binomial?
Why are these trees called binomial?
Hint: how many nodes at
Why Binomial?
Why are these trees called binomial?
Hint: how many nodes at
Definition of Binomial Queues
3
Binomial Queue = “forest” of heap-ordered binomial trees
1
7
-1
2
1
3
8
11
5
6
5
9
6
7
21
B0
Definition of Binomial Queues
3
Binomial Queue = “forest” of heap-ordered binomial trees
1
7
-1
2
1
3
8
11
5
6
5
9
6
7
21
B0
Binomial Queue Properties
Suppose you are given a binomial queue of N
Binomial Queue Properties
Suppose you are given a binomial queue of N
Binomial Queues: Merge
Main Idea: Merge two binomial queues by merging individual
Binomial Queues: Merge
Main Idea: Merge two binomial queues by merging individual
Example: Binomial Queue Merge
Merge H1 and H2
3
1
7
-1
2
1
3
8
11
5
6
5
9
6
7
21
H1: H2:
Example: Binomial Queue Merge
Merge H1 and H2
3
1
7
-1
2
1
3
8
11
5
6
5
9
6
7
21
H1: H2:
Example: Binomial Queue Merge
Merge H1 and H2
3
1
7
-1
2
1
3
8
11
5
6
5
9
6
7
21
H1: H2:
Example: Binomial Queue Merge
Merge H1 and H2
3
1
7
-1
2
1
3
8
11
5
6
5
9
6
7
21
H1: H2:
Example: Binomial Queue Merge
Merge H1 and H2
3
1
7
-1
2
1
3
8
11
5
6
5
9
6
7
21
H1: H2:
Example: Binomial Queue Merge
Merge H1 and H2
3
1
7
-1
2
1
3
8
11
5
6
5
9
6
7
21
H1: H2:
Example: Binomial Queue Merge
Merge H1 and H2
3
1
7
-1
2
1
3
8
11
5
6
5
9
6
7
21
H1: H2:
Example: Binomial Queue Merge
Merge H1 and H2
3
1
7
-1
2
1
3
8
11
5
6
5
9
6
7
21
H1: H2:
Example: Binomial Queue Merge
Merge H1 and H2
3
1
7
-1
2
1
3
8
11
5
6
5
9
6
7
21
H1: H2:
Example: Binomial Queue Merge
Merge H1 and H2
3
1
7
-1
2
1
3
8
11
5
6
5
9
6
7
21
H1: H2:
Example: Binomial Queue Merge
Merge H1 and H2
3
1
7
-1
2
1
3
8
11
5
6
5
9
6
7
21
H1: H2:
Example: Binomial Queue Merge
Merge H1 and H2
3
1
7
-1
2
1
3
8
11
5
6
5
9
6
7
21
H1: H2:
Example: Binomial Queue Merge
Merge H1 and H2
3
1
7
-1
2
1
3
8
11
5
6
5
9
6
7
21
H1: H2:
Example: Binomial Queue Merge
Merge H1 and H2
3
1
7
-1
2
1
3
8
11
5
6
5
9
6
7
21
H1: H2:
Example: Binomial Queue Merge
Merge H1 and H2
3
1
7
-1
2
1
3
8
11
5
6
5
9
6
7
21
H1: H2:
Example: Binomial Queue Merge
Merge H1 and H2
3
1
7
-1
2
1
3
8
11
5
6
5
9
6
7
21
H1: H2:
Example: Binomial Queue Merge
Merge H1 and H2
3
1
7
-1
2
1
3
8
11
5
6
5
9
6
7
21
H1: H2:
Example: Binomial Queue Merge
Merge H1 and H2
3
1
7
-1
2
1
3
8
11
5
6
5
9
6
7
21
H1: H2:
Binomial Queues: Merge and Insert
What is the run time for Merge
Binomial Queues: Merge and Insert
What is the run time for Merge
Binomial Queues: Merge and Insert
What is the run time for Merge
Binomial Queues: Merge and Insert
What is the run time for Merge
Insert 1,2,…,7
1
Insert 1,2,…,7
1
Insert 1,2,…,7
1
2
Insert 1,2,…,7
1
2
Insert 1,2,…,7
1
2
3
Insert 1,2,…,7
1
2
3
Insert 1,2,…,7
1
2
3
4
Insert 1,2,…,7
1
2
3
4
Insert 1,2,…,7
1
2
3
4
Insert 1,2,…,7
1
2
3
4
Insert 1,2,…,7
1
2
3
4
5
Insert 1,2,…,7
1
2
3
4
5
Insert 1,2,…,7
1
2
3
4
5
6
Insert 1,2,…,7
1
2
3
4
5
6
Insert 1,2,…,7
1
2
3
4
5
6
7
Insert 1,2,…,7
1
2
3
4
5
6
7
Binomial Queues: DeleteMin
Steps:
Find tree Bk with the smallest root
Remove Bk from
Binomial Queues: DeleteMin
Steps:
Find tree Bk with the smallest root
Remove Bk from
Insert 1,2,…,7
1
2
3
4
5
6
7
Insert 1,2,…,7
1
2
3
4
5
6
7
DeleteMin
2
3
4
5
6
7
DeleteMin
2
3
4
5
6
7
Merge
2
3
4
5
6
7
Merge
2
3
4
5
6
7
Merge
2
3
4
5
6
7
Merge
2
3
4
5
6
7
Merge
2
3
4
5
6
7
Merge
2
3
4
5
6
7
Merge
2
3
4
5
6
7
DONE!
Merge
2
3
4
5
6
7
DONE!
Implementation of Binomial Queues
Need to be able to scan through all
Implementation of Binomial Queues
Need to be able to scan through all
Other Mergeable Priority Queues:
Leftist and Skew Heaps
Leftist Heaps: Binary heap-ordered
Other Mergeable Priority Queues:
Leftist and Skew Heaps
Leftist Heaps: Binary heap-ordered
Золотое сечение в архитектуре, скульптуре, живописи
Собственность
Презентация "Тренды и бренды" - скачать презентации по Экономике
Микропроцессоры: классификация, архитектура, система команд
Робота з датчиком кольору
POLYCASE 2019. Чемпионат по решению реальной производственной задачи
Кто во что горазд - презентация для начальной школы_
Ультразвук: джерела та застосування
Социальная природа международного терроризма в современном мире
Пасха. Символы Пасхи
Основы С#. Платформа Microsoft.NET. Основные понятия. Пространство имен. (Лекция 1)
Классификация машинных команд
Права и свободы человека и гражданина
Директивы в Angular
Технология личностно-ориентированного обучения
EARLY MODERN ENGLISH PHONOLOGICAL AND MORPHOLOGICAL SYSTEM
Общероссийский конкурс «Мой бизнес- моя Россия» – “открытая мастерская” Центр Изобретений
Подведём итоги
Суды и правосудие
Безопасность интернет-проекта. Основные угрозы. Инструменты безопасности в платформе
Символика УР 
Сравнительный анализ культурного туризма в республике Молдова и Румынии
Организация междугородных экскурсионных маршрутов в туристической фирме «Форитур»
Развод и последующий за ним раздел имущества
Гигиена труда в термических цехах
Организационные основы управления информационной безопасностью
Презентация "Оценка эффективности" - скачать презентации по Экономике
Муниципальное общеобразовательное учреждение «Тевризская средняя общеобразовательная школа №1» Тевризского муниципального р