Деревья. Идеально сбалансированные бинарные деревья

Бинарное дерево назовем идеально сбалансированным, если для каждой его вершины количество вершин в

Длина внутреннего пути в идеально сбалансированном дереве, содержащем n вершин, не

взять одну вершину в качестве корня.
построить левое поддерево с nl = n

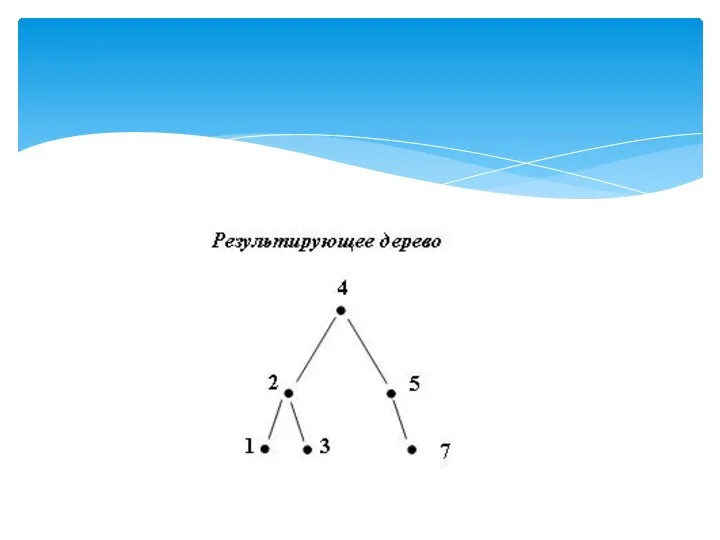
node *Tree (int n, node **p)
// Построение идеально сбалансированного дерева с

Бинарное дерево поиска называется балансированным по высоте, если для каждой его вершины высота

бозначим Th - АВЛ-деpево высотой h с количеством узлов Nh. Тогда

Математический анализ АВЛ-деpевьев

Теоpема 

Hаибольшая длина ветвей (h+1) в АВЛ-деpеве, содеpжащем Nh узлов, опpеделяется неравенством

Лемма 

Hаименьшая длина ветвей (h+1) в АВЛ-деpеве, содеpжащем Nh узлов опpеделяется фоpмулойh+1=log2(Nh+1)

Лемма 

Пусть Th - АВЛ-деpево высоты h, имеющее Nh узлов. Тогда для средней длины ветвей дерева Sh пpи имеет место следующая

Hаиболее асимметpичное АВЛ-деpево Th высоты h имеет наиболее асимметpичное АВЛ-деpевоTh-1 высоты h-1 в качестве одного из своих поддеpевьев и наиболее

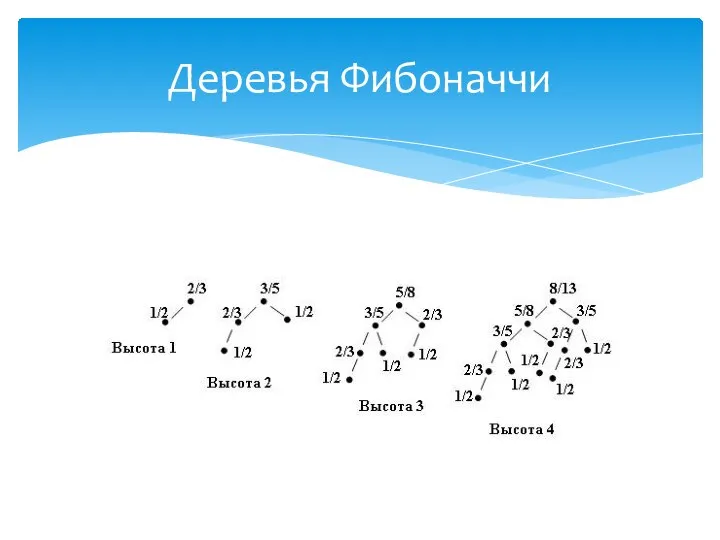
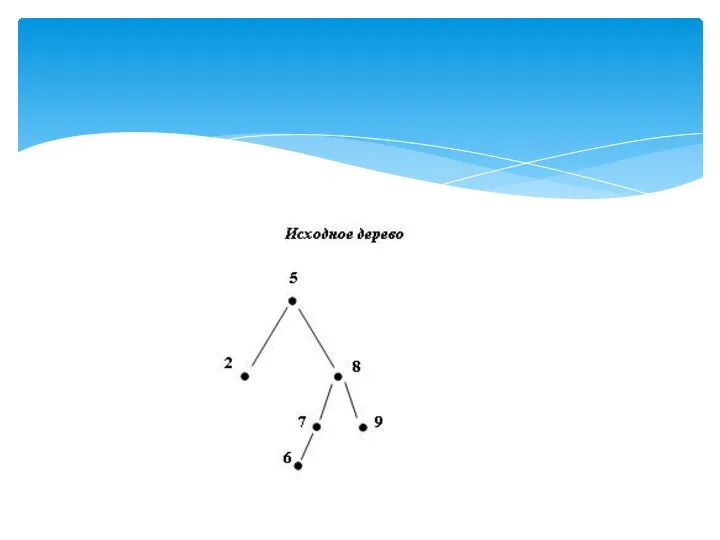
если k=0, то дерево Фибоначчи пусто;
если k=1, то дерево Фибоначчи состоит из единственного узла,

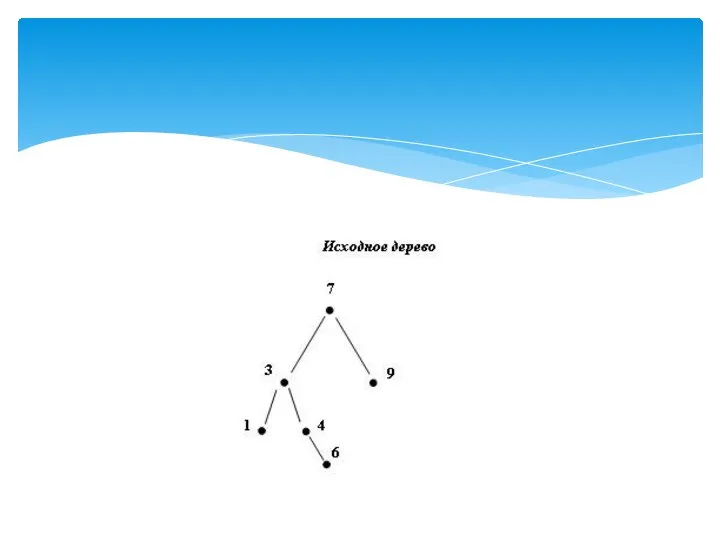
Приммер деpевьев Фибоначчи

показатель сбалансиpованности узла = = высота пpавого поддеpева - высота левого

Класс бинарных деревьев, в которых ограничения на высоты поддеревьев заменено ограничением

Корневым балансом b(Tn) бинарного дерева Tn=(Tl,v,Tr) называется величина
nl+1  
b(Tn)=-------, n >= 1
n+1
0 <

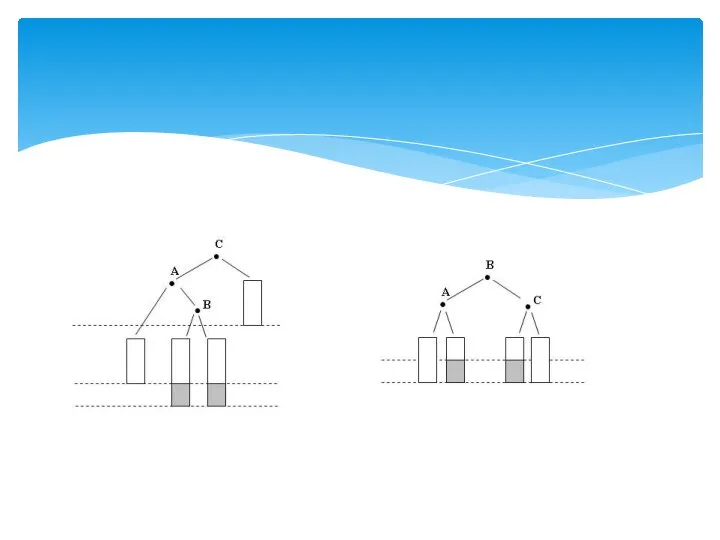
Дерево Tn называется балансированным по весу с балансом  A, 0< A < 1/2, если оно

Класс бинарных деревьев с балансом A - WB[A].
Пустое бинарное дерево T0, по определению, входит

Деревья Фибоначчи

Высота дерева Tn из класса WB[A] не превышает

Теорема

высота дерева Фибоначчи не превышает log2(n+1)-1

сначала было hL = hR. После включения L и R станут разной высоты, но критерий сбалансированности не

struct node
{
int Key;
int Count;
int bal; //

Показатель сбалансированности вершины = разность между высотой правого и левого поддерева

Определение

Проход по дереву, чтобы убедиться, что включаемого значения в дереве нет;
включение

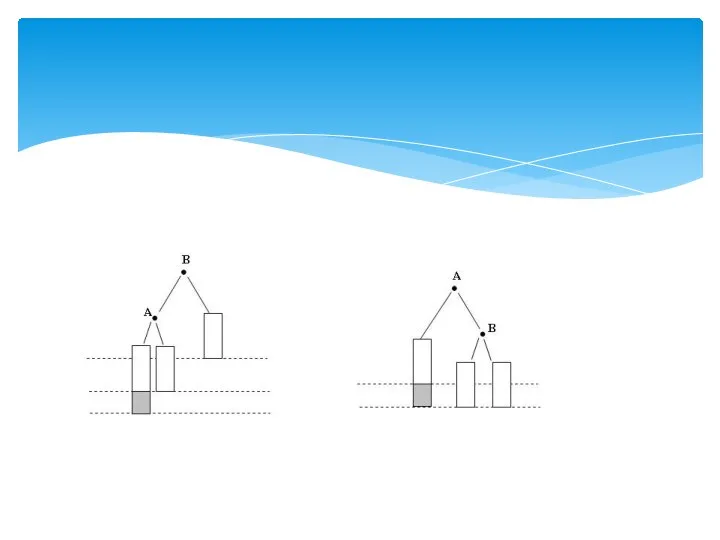
p1 = (*p).Left;
(*p).Left = (*p1).Right;
(*p1).Right = p;
(*p).bal =

LL-поворот

p1 = (*p).Left;
(*p).Left = (*p1).Right;
(*p1).Right = p;
(*p).bal =

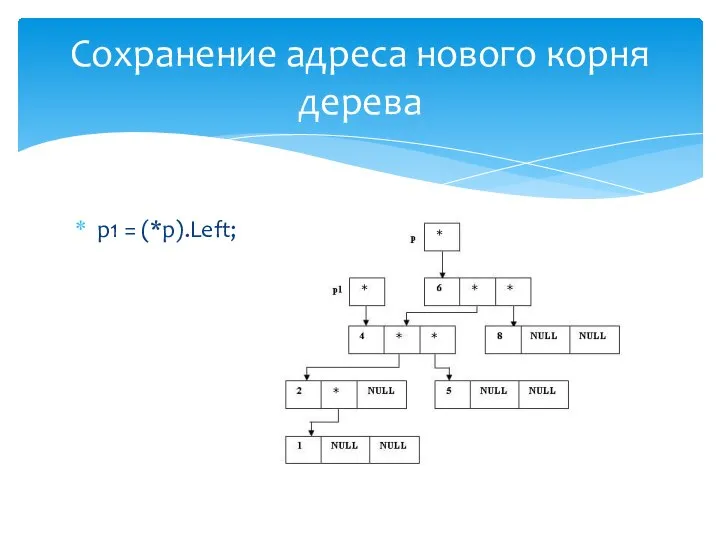
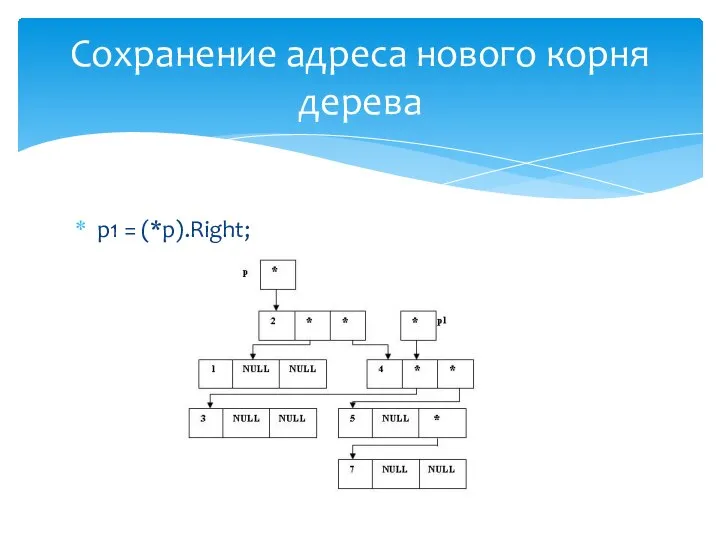
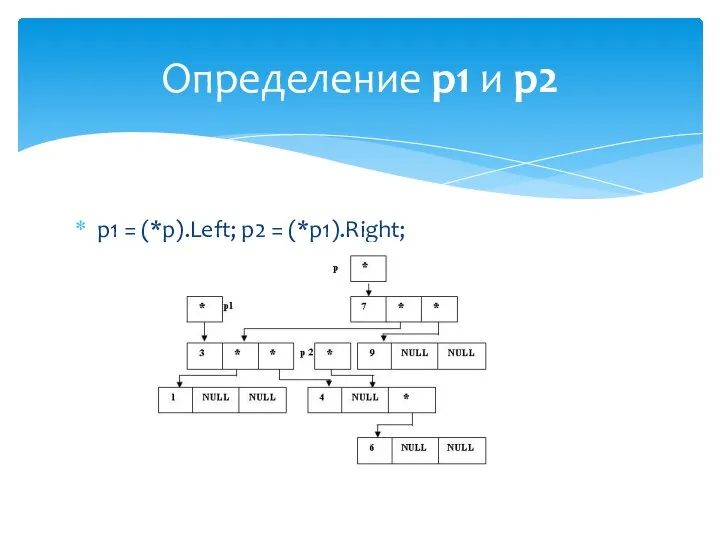
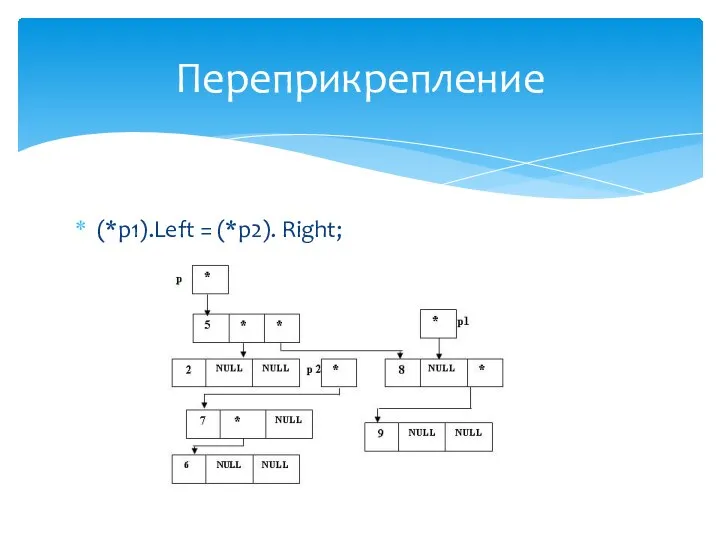
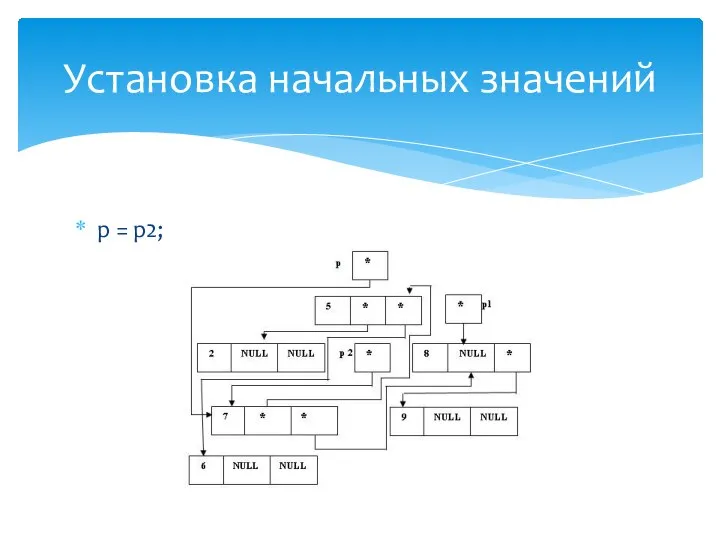
p1 = (*p).Left;

Сохранение адреса нового корня дерева

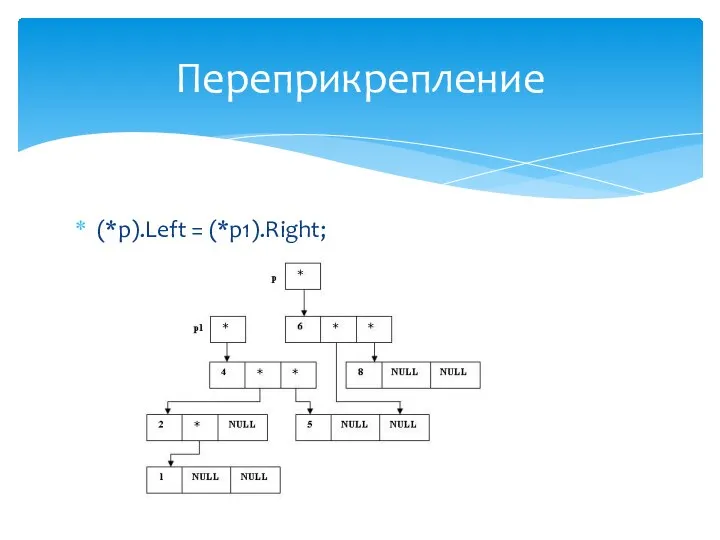
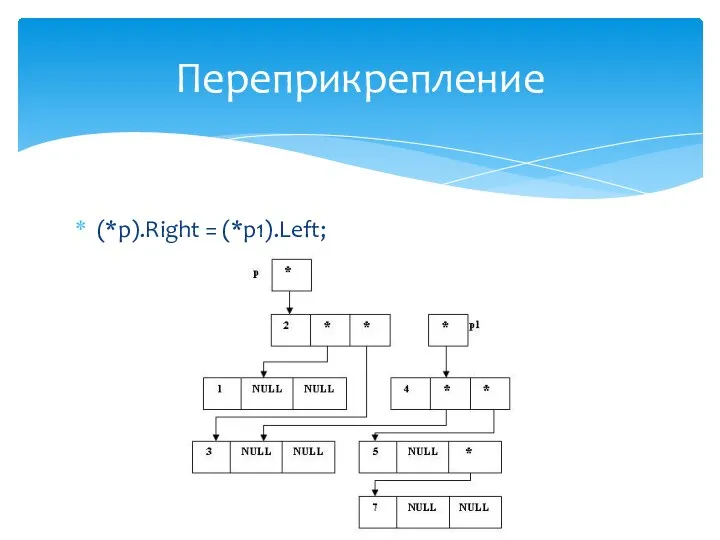
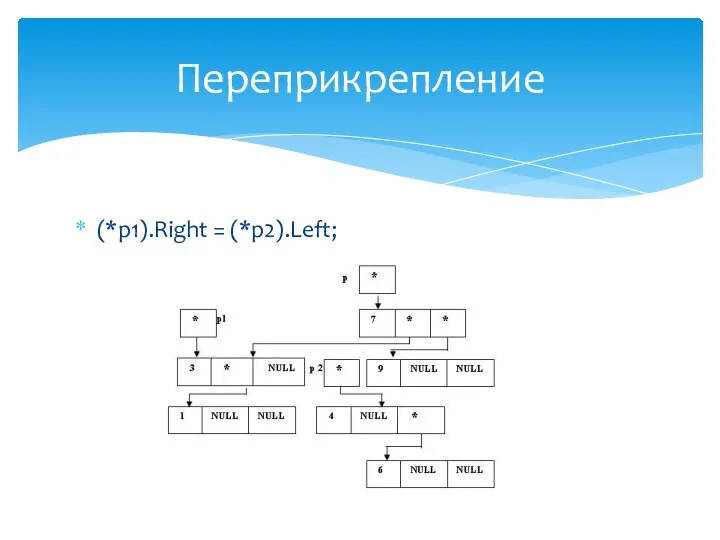
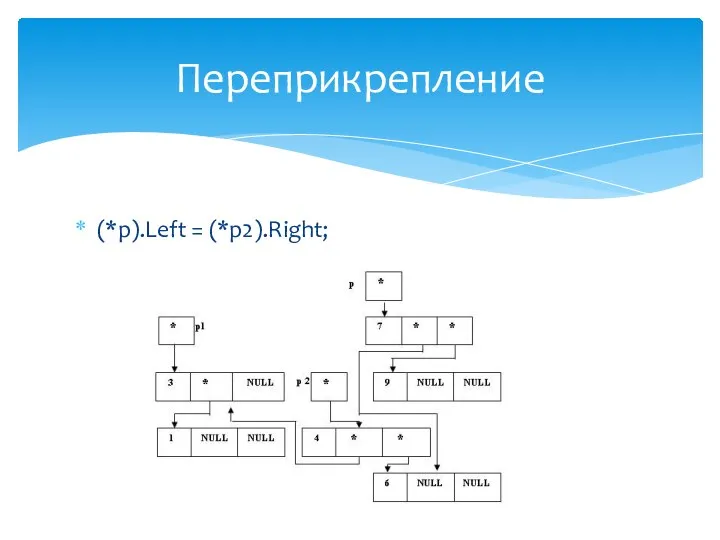
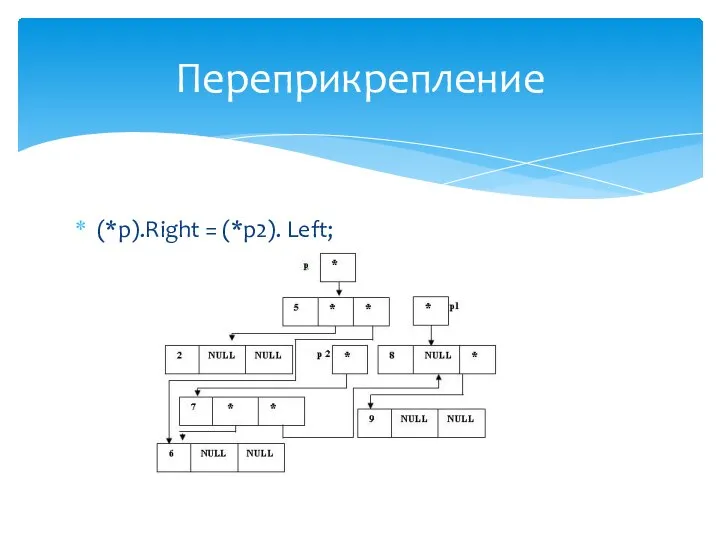
(*p).Left = (*p1).Right;

Переприкрепление

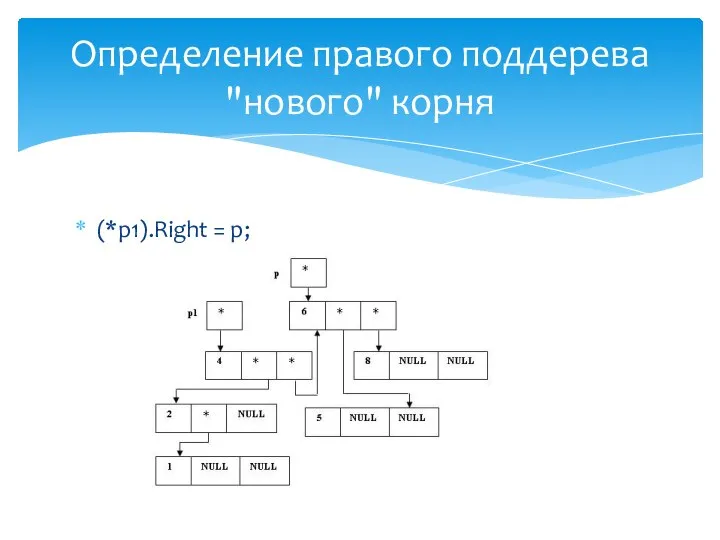
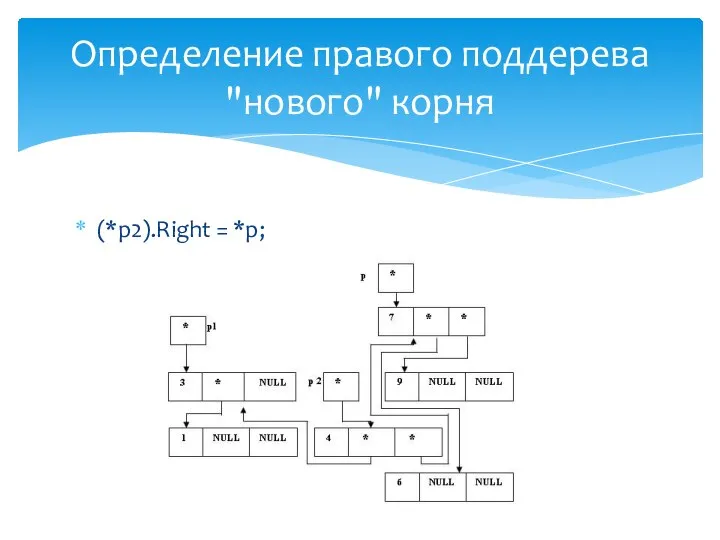
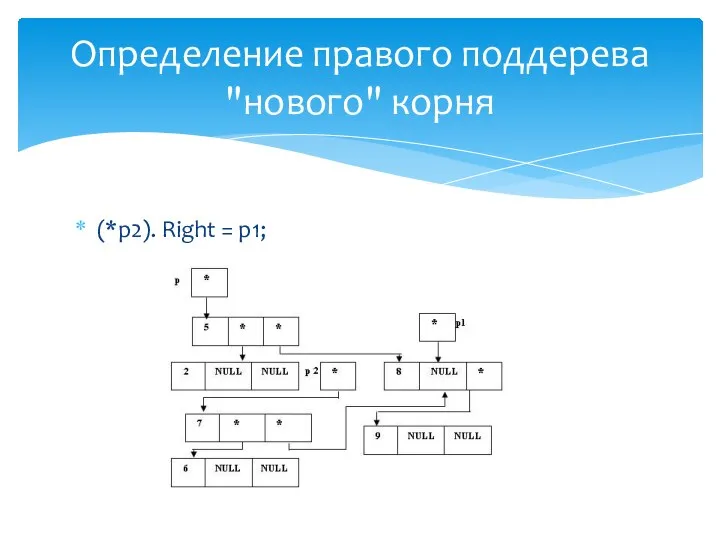
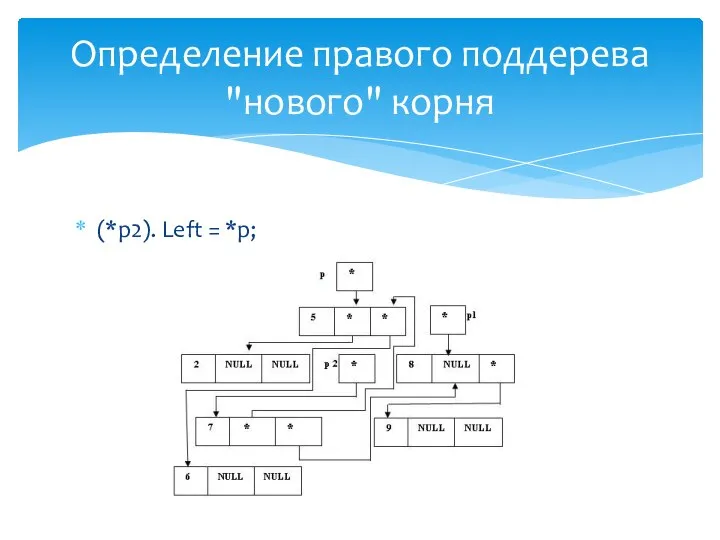
(*p1).Right = p;

Определение правого поддерева "нового" корня

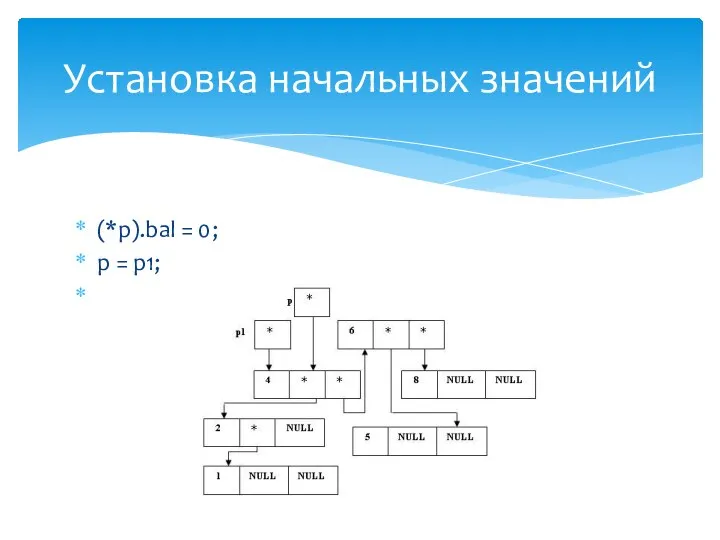
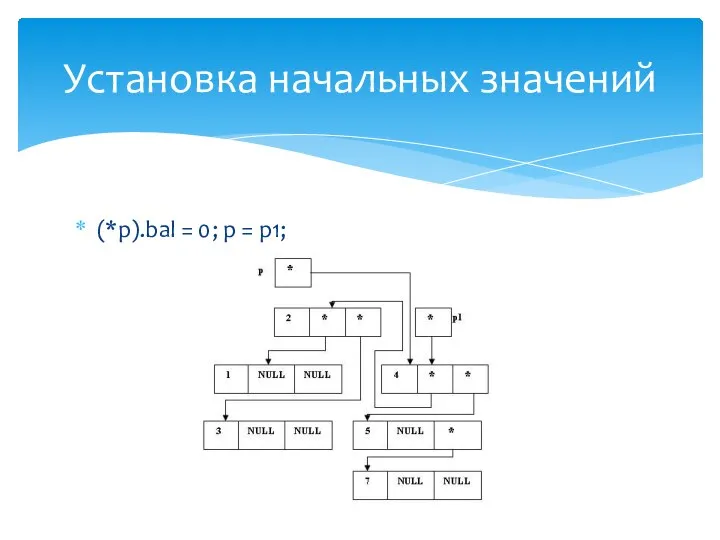
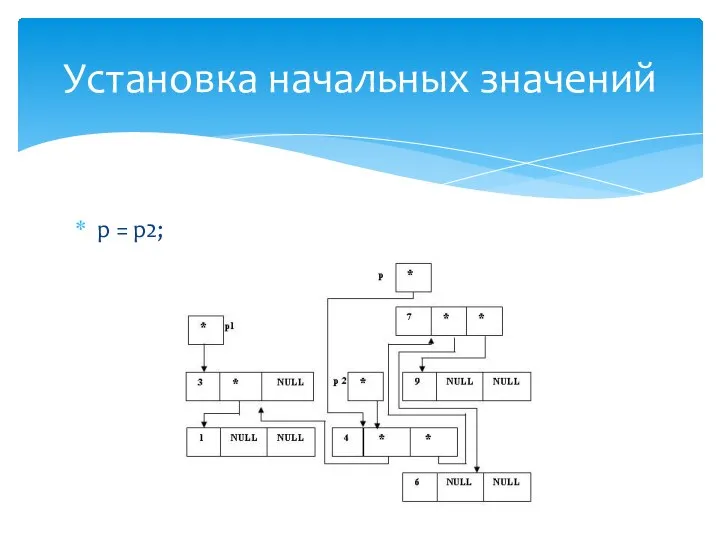
(*p).bal = 0;
p = p1;

Установка начальных значений

p1 = (*p).Right;
(*p).Right = (*p1).Left;
(*p1).Left = p;
(*p).bal

p1 = (*p).Right;

Сохранение адреса нового корня дерева

(*p).Right = (*p1).Left;

Переприкрепление

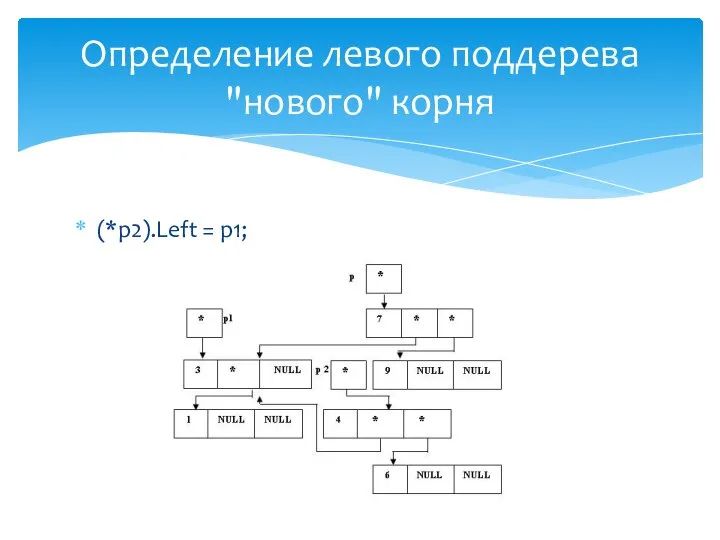
(*p1).Left = p;

Определение левого поддерева "нового" корня

(*p).bal = 0; p = p1;

Установка начальных значений

Если после вставки показатели сбалансированности вершин имеют одинаковый знак и отличаются

p1 = (*p).Left;
p2 = (*p1).Right;
(*p1).Right = (*p2).Left;
(*p2).Left

p1 = (*p).Left; p2 = (*p1).Right;

Определение p1 и p2

(*p1).Right = (*p2).Left;

Переприкрепление

(*p2).Left = p1;

Определение левого поддерева "нового" корня

(*p).Left = (*p2).Right;

Переприкрепление

(*p2).Right = *p;

Определение правого поддерева "нового" корня

p = p2;

Установка начальных значений

p1 =(*p).Right; p2 = (*p1).Left;
(*p1).Left = (*p2). Right; (*p2).

p1 = (*p).Right; p2 = (*p1).Left;

Определение p1 и p2

(*p1).Left = (*p2). Right;

Переприкрепление

(*p2). Right = p1;

Определение правого поддерева "нового" корня

(*p).Right = (*p2). Left;

Переприкрепление

(*p2). Left = *p;

Определение правого поддерева "нового" корня

p = p2;

Установка начальных значений

Если после вставки показатели сбалансированности имеют разный знак, то можно восстановить

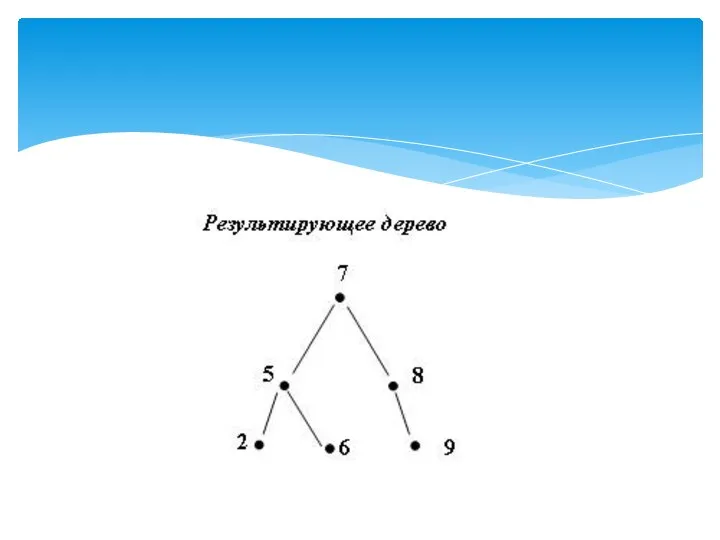
Построение AVL дерева