Двойственный симплекс-метод

Введение

Рассмотрим следующую задачу линейного программирования (ЗЛП):

Приведем рассматриваемую ЗЛП к каноническому виду:

или

Рассмотрим расширенную
матрицу системы
линейных уравнений:
Матрица содержит единичную подматрицу порядка 3 и

Так как элементы (n+1=6)-го столбца матрицы системы не являются неотрицательными, то

В чем отличие двойственного симплекс-метода от обычного??
При решении задачи симплекс-методом текущее

КЗЛП имеет вид:

Р-матрица. Определение

Р-матрицей КЗЛП (1) –(3) называется расширенная матрица системы линейных уравнений,

Условие перехода от одной Р-матрицы ЗЛП к другой
Пусть известна Р-матрица ,

Теорема 1:

Пусть и в строке матрицы есть хотя бы один отрицательный

Теорема 2:

Пусть и в строке матрицы нет ни одного отрицательного элемента.

Теорема 3:

При переходе от матрицы к матрице целевая функция изменяется в

Алгоритм Р-метода

Будем считать, что известна исходная Р- матрица задачи линейного программирования,

Рассмотрим алгоритм S-ой итерации метода последовательного уточнения оценок. В начале S-ой

ШАГ 2. Если , то псевдоплан
является оптимальным опорным планом, а
есть

ШАГ 3. Если то задача линейного программирования не имеет решения (множество

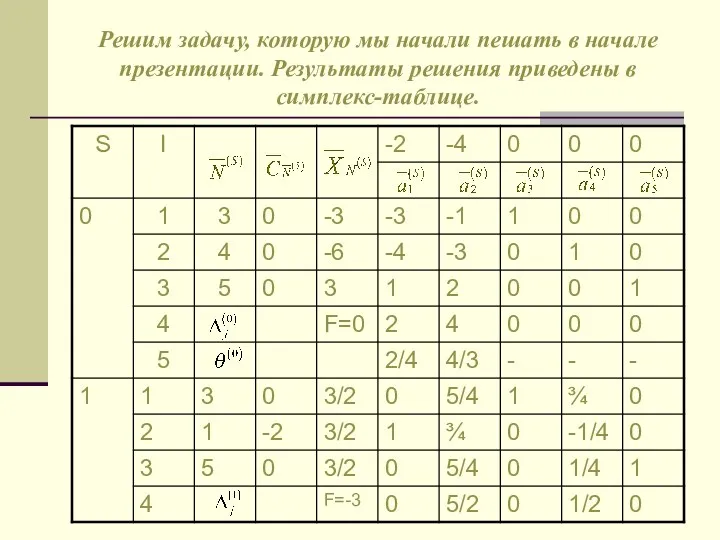
Решим задачу, которую мы начали пешать в начале презентации. Результаты решения

Решим следующую ЗЛП:

Приводим ЗЛП к каноническому виду

Т.К. расширенная матрица

системы линейных уравнений является Р-матрицей.

Следовательно, к решению данного ЗЛП

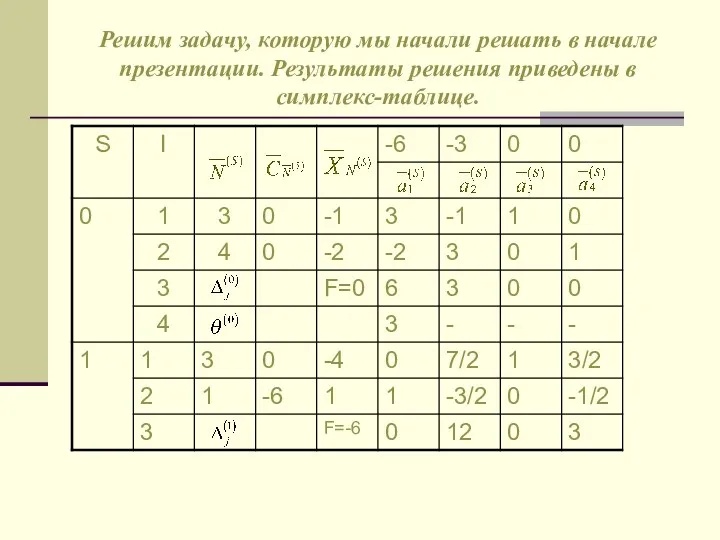
Решим задачу, которую мы начали решать в начале презентации. Результаты решения