Содержание
- 2. Закон Кулона. (1785). Векторная запись закона Кулона для точечных зарядов в вакууме имеет вид (см. рис.
- 3. 2.Электростатическое поле. Напряженность поля. Электростатическое поле – это поле, созданное покоящимися электрическими зарядами Взаимодействие между неподвижными
- 4. Рассмотрим поле точечного заряда. Возьмем точечный заряд Q и найдем напряженность поля этого заряда в произвольной
- 5. Электростатическое поле можно описать, с помощью линий напряженности, которые называют линиями вектора или силовыми линиями. Силовой
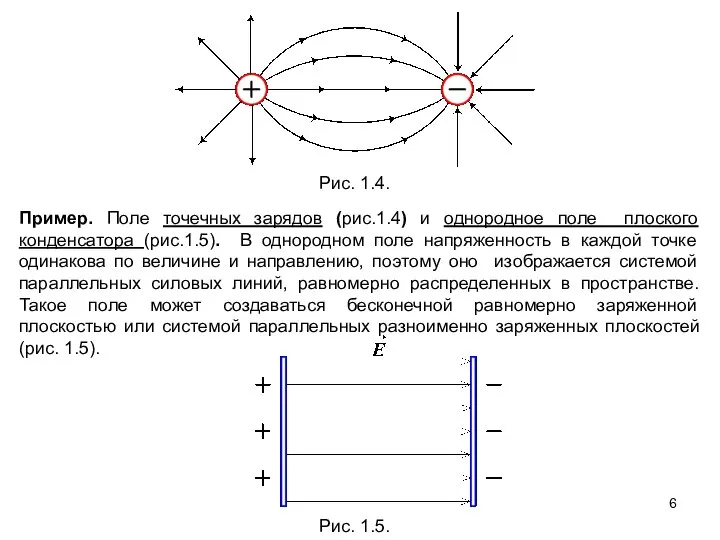
- 6. Рис. 1.4. Пример. Поле точечных зарядов (рис.1.4) и однородное поле плоского конденсатора (рис.1.5). В однородном поле
- 7. 3. Принцип суперпозиции электростатических полей Пусть имеется система точечных зарядов , создающих поле. Поместим в точку
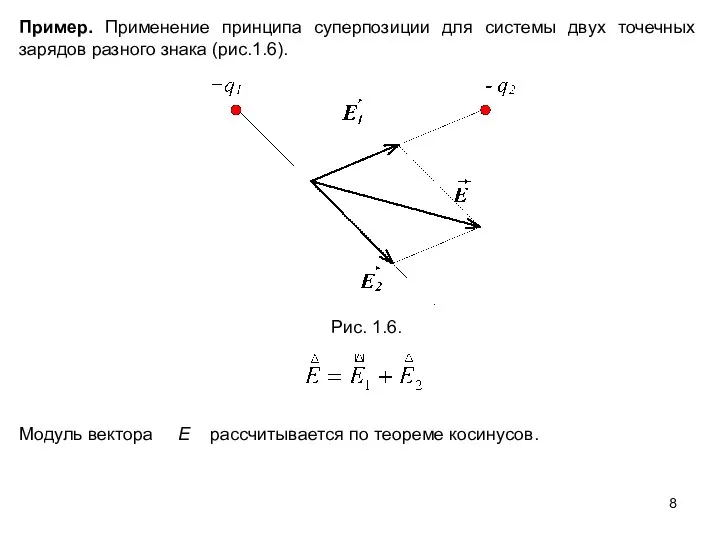
- 8. Пример. Применение принципа суперпозиции для системы двух точечных зарядов разного знака (рис.1.6). Рис. 1.6. Модуль вектора
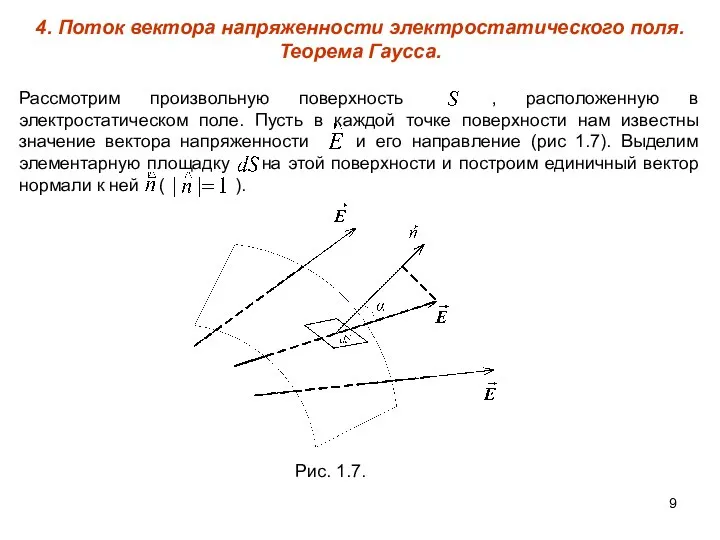
- 9. 4. Поток вектора напряженности электростатического поля. Теорема Гаусса. Рассмотрим произвольную поверхность , расположенную в электростатическом поле.
- 10. Потоком вектора через замкнутую поверхность называется интеграл: (9) Согласно свойствам скалярного произведения векторов интеграл (9) можно
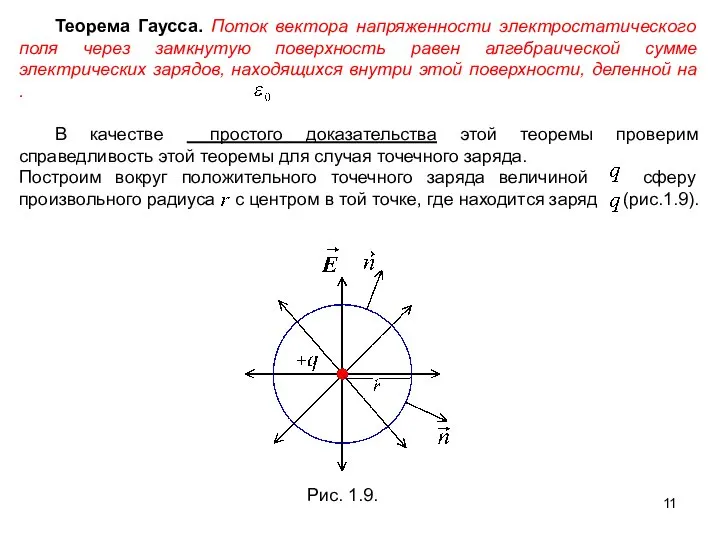
- 11. Теорема Гаусса. Поток вектора напряженности электростатического поля через замкнутую поверхность равен алгебраической сумме электрических зарядов, находящихся
- 12. Следовательно, в любой точке построенной сферической поверхности напряженность поля одинакова и равна Вектор перпендикулярен поверхности сферы,
- 13. Итак, теорема Гаусса для электростатического поля в вакууме в интегральной форме для любого количества зарядов внутри
- 14. Выражение слева называется дивергенцией вектора : обозначают Дивергенция в декартовых координатах вычисляется по формуле: Итак, в
- 15. 5. Применение теоремы Гаусса к расчету полей заряженных тел. 1. Заряженная равномерно по поверхности сфера. Рассмотрим
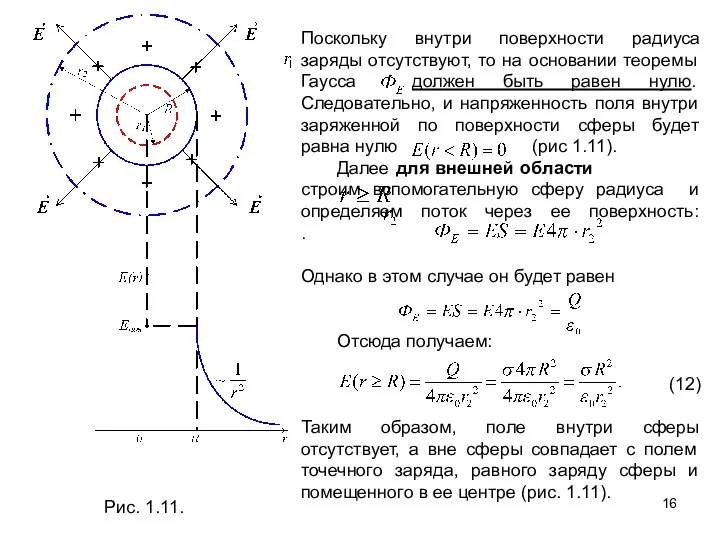
- 16. Рис. 1.11. Поскольку внутри поверхности радиуса заряды отсутствуют, то на основании теоремы Гаусса должен быть равен
- 18. Скачать презентацию










 Презент книги
Презент книги Элементы беспроводного управления электронных устройств на базе Arduino
Элементы беспроводного управления электронных устройств на базе Arduino Происхождение и этническая принадлежность венгров
Происхождение и этническая принадлежность венгров Құқыққа сай әрекеттердің түрлері. Құқықбұзушылық құқыққа қарсы әрекет ретінде. Заңды жауапкершіліктің белгілері
Құқыққа сай әрекеттердің түрлері. Құқықбұзушылық құқыққа қарсы әрекет ретінде. Заңды жауапкершіліктің белгілері Сказки Тукая - презентация для начальной школы
Сказки Тукая - презентация для начальной школы Аттестационная работа. «Исследование структурированных операторов и простых типов данных языка программирования Pascal»
Аттестационная работа. «Исследование структурированных операторов и простых типов данных языка программирования Pascal» Презентация "Производственная логистика" - скачать презентации по Экономике
Презентация "Производственная логистика" - скачать презентации по Экономике Česká rodina
Česká rodina Дом с призраком. Часть первая
Дом с призраком. Часть первая Зелёный пояс Славы Монументы Большого блокадного кольца – самые близкие к Ленинграду рубежи, где были остановлены фашистские вой
Зелёный пояс Славы Монументы Большого блокадного кольца – самые близкие к Ленинграду рубежи, где были остановлены фашистские вой Вежливая паутина Куда пропадает нравственность в Интернете?
Вежливая паутина Куда пропадает нравственность в Интернете?  Комуністична партія України
Комуністична партія України Презентация Нотариально удостоверенное завещание
Презентация Нотариально удостоверенное завещание Пример программы оформления договора страхования на портале продаж и на сайте компании © ООО «Капитал Лайф Страхование Жизни
Пример программы оформления договора страхования на портале продаж и на сайте компании © ООО «Капитал Лайф Страхование Жизни Инженерные коммуникации в доме. 8 класс
Инженерные коммуникации в доме. 8 класс Предпринимательство
Предпринимательство Управление персоналом на авиапредприятиях
Управление персоналом на авиапредприятиях Презентация Понятие и предмет административного права
Презентация Понятие и предмет административного права Play go and grow
Play go and grow Свет и освещение
Свет и освещение Презентация Эволюционистская концепция происхождения культуры
Презентация Эволюционистская концепция происхождения культуры Театр - презентация для начальной школы
Театр - презентация для начальной школы Кроссворд Концепции современного естествознания
Кроссворд Концепции современного естествознания Складской технологический процесс. Операции по поступлению товаров
Складской технологический процесс. Операции по поступлению товаров Апаратура обчислювальних засобів. Оперативний запам’ятовуючий пристрій (Заняття № 7.7)
Апаратура обчислювальних засобів. Оперативний запам’ятовуючий пристрій (Заняття № 7.7) Гидрологические факторы деградации почв и способ их защиты
Гидрологические факторы деградации почв и способ их защиты  Дед Мороз - презентация для начальной школы
Дед Мороз - презентация для начальной школы Green logistics
Green logistics