Содержание
- 2. Модульная арифметика a=cn+res(a) Переместительный закон (коммутативный) (a+b)(modn)=(b+a)(modn) r=a(modn) Сочетальный закон (ассоциативный) (a+(b+c))(modn)=((a+b)+c)(modn) Распределительный закон a(b+c)(modn)=ab(modn)+ac(modn) (a+b)(modn)=[a(modn)+b(modn)](modn)
- 3. Разложение на множители Число p называется простым, если оно не имеет делителей кроме тривиальных (1,-1, p,
- 4. Наибольший общий делитель Наибольшим общим делителем (НОД) двух чисел v и u называется наибольшее целое число,
- 5. Теоремы Эйлера и Ферма Функция Эйлера ϕ(x). Определяет число натуральных чисел меньших x и взаимно простых
- 6. Обращение элемента по модулю n Обратный элемент x к числу a - это такое целое число,
- 7. Пример нахождения обратного элемента n=17, a=13, a-1=? 1. используя алгоритм Евклида, находим НОД(17,13), 17=1*13+4 13=3*4+1, НОД=1
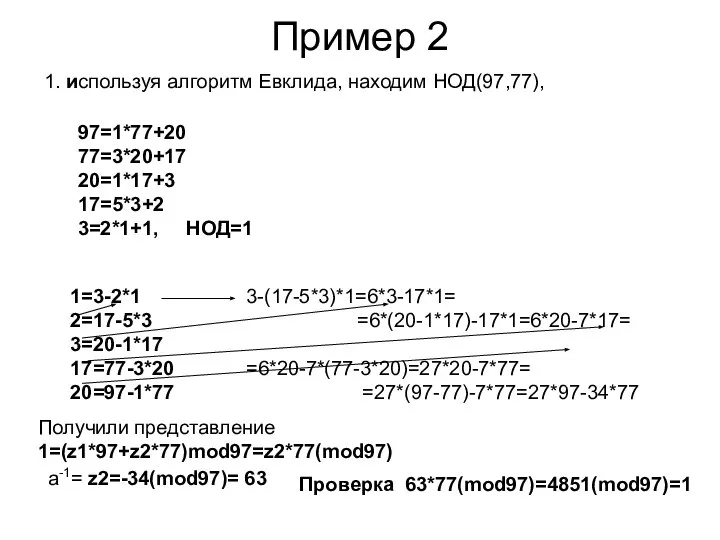
- 8. Пример 2 1. используя алгоритм Евклида, находим НОД(97,77), 97=1*77+20 77=3*20+17 20=1*17+3 17=5*3+2 3=2*1+1, НОД=1 1=3-2*1 2=17-5*3
- 10. Возведение в степень y=ax(modn) Прямой способ: a·a·…a·a(modn) 1. Быстрый способ возведения: Пример: 337(mod7) Представим показатель степени
- 11. Возведение в степень 2. Быстрый способ возведения Д.Кнута. - представим показатель степени в двоичном виде; -
- 12. Вычисление дискретного логарифма logay=x(modn) y=ax(modn) Сложность вычислений для операции дискретного логарифмирования: N≅O((n)1/2). Нахождение дискретного логарифма методом
- 13. Проверка чисел на простоту Тест Ферма (вероятностный тест). В его основе лежит теорема Ферма, т. е.
- 14. Тест Ферма Пример. n=341, b=2. 2340=(210)34mod341=(1024(mod341))10(mod341)=1. Но с другой стороны 341=31⋅11, т.е. число составное. Для любого
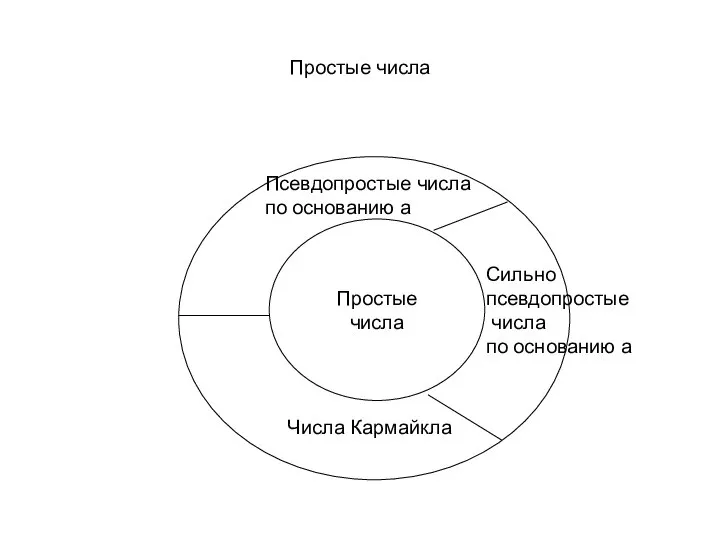
- 15. Простые числа Простые числа Числа Кармайкла Псевдопростые числа по основанию а Сильно псевдопростые числа по основанию
- 16. Пусть число n нечетное и n − 1 = 2sr, где r — нечетное. a –
- 17. Тест Рабина- Миллера - Тест-Рабина-Миллера позволяет отсеять часть псевдопростых чисел Вероятность ошибки для Теста Рабина-Миллера P(n-составное)
- 18. Тест Миллера - Рабина Пусть число n нечетное и n − 1 = 2sr, где r
- 20. Скачать презентацию















 Федор Александрович Васильев Подготовила ученица 10 класса Бутикова Мария
Федор Александрович Васильев Подготовила ученица 10 класса Бутикова Мария Основы чир спорта
Основы чир спорта Семибратова О.П.
Семибратова О.П.  Sport & Healthy Way of Living
Sport & Healthy Way of Living Роль политики в жизни общества
Роль политики в жизни общества Создание системы предупреждения потопа
Создание системы предупреждения потопа Известные лыжники России
Известные лыжники России Корпоративное право
Корпоративное право ФУНКЦИОНАЛЬНЫЙ ГЕНЕРАТОР
ФУНКЦИОНАЛЬНЫЙ ГЕНЕРАТОР Государство - это организация политической власти,
Государство - это организация политической власти, Мировая экономика
Мировая экономика  Австралия мен Океания халықтарының орналасуы мен этникалық құрамы
Австралия мен Океания халықтарының орналасуы мен этникалық құрамы Коррекция физического развития, двигательной и функциональной подготовленности средствами физической культуры и спорта. (Тема 3)
Коррекция физического развития, двигательной и функциональной подготовленности средствами физической культуры и спорта. (Тема 3) Содержание: 1. Определение термина «телеконференция». Определение термина «телеконференция» 2. АудиоконференцияАудиоконференция
Содержание: 1. Определение термина «телеконференция». Определение термина «телеконференция» 2. АудиоконференцияАудиоконференция  Конструкции валов и осей
Конструкции валов и осей  Натюрморт в графике Натюрмо́рт — изображение неодушевлённых предметов в изобразительном искусстве, в отличие от пор
Натюрморт в графике Натюрмо́рт — изображение неодушевлённых предметов в изобразительном искусстве, в отличие от пор Игра футбол
Игра футбол Пересмотр судебных постановлений в апелляционном порядке
Пересмотр судебных постановлений в апелляционном порядке Модуляция и демодуляция
Модуляция и демодуляция Bid OUt
Bid OUt Подготовка к многодневному походу
Подготовка к многодневному походу A Brief History of Tennis
A Brief History of Tennis Параллельное программирование. Лекция 1
Параллельное программирование. Лекция 1 Интернет. Общие сведения. Адресация в Интернет
Интернет. Общие сведения. Адресация в Интернет Историческая трансформация сотового телефона
Историческая трансформация сотового телефона Презентация Понятие методологии ценообразования
Презентация Понятие методологии ценообразования Лекция 4 Энергетическая безопасность России
Лекция 4 Энергетическая безопасность России  Департамент образования администрации г. Липецка Муниципальное бюджетное образовательное учреждение дополнительного образо
Департамент образования администрации г. Липецка Муниципальное бюджетное образовательное учреждение дополнительного образо