Элементы матричной алгебры

1.2. Операции с матрицами и их свойства

Равенство матриц.

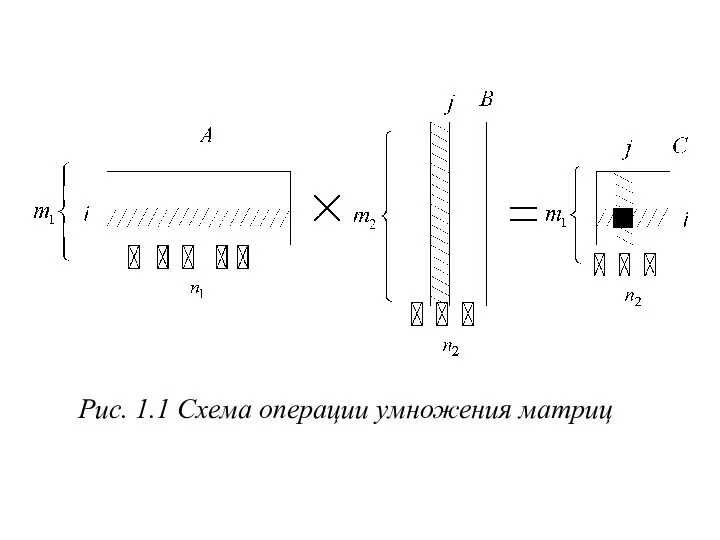
Согласно (1.8) элемент Cij равен сумме
произведений элементов строки i матрицы

Рис. 1.1 Схема операции умножения матриц

Пример 1.4. Найти произведение

Пример 1.5. Найти произведение квадратной
матрицы и вектор–столбца.

Произведение двух матриц не обладает
переместительным свойством:

,

в чем можно убедиться на

1.3. Определитель матрицы

.

. (1.10)

Пример 1.6. Вычислить определитель 3-го порядка

Линейная зависимость и линейная комбинация
элементов матрицы
Запишем два столбца:

,

Свойства определителей

1. Равноправие строк и столбцов

2. Если все элементы какого-либо столбца

4. Определитель с двумя одинаковыми столбцами
(строками) равен нулю:

5. Если какой-либо

1.4. Алгебраические дополнения и миноры

Рассмотрим определитель D 3-го порядка (n =

Алгебраическое дополнение

На рис.1.1 показаны знаки сомножителя (-1)i+j
для определителя 3-го

Пример 1.9. Проверить, что для треугольных
матриц определитель равен произведению

1.5. Обратная матрица

Обратной матрицей A-1 по отношению к исходной A

Обращение матрицы можно осуществить
по следующему правилу.

1. Вычислить определитель исходной

Пример 1.10. Произвести обращение матрицы

и доказать, что она обратная.

Решение

Доказательство: Если A-1 – обратная матрица,
то справедливо выражение AA-1

1.6. Системы линейных алгебраических уравнений

Предположим, что задана система m линейных

Примером системы, обладающей единственным
решением является, например:

Пример 1.11. Решить линейную систему 3-х
уравнений с 4-мя неизвестными