Содержание
- 2. Пусть задана система n линейных уравнений с n неизвестными
- 3. Совокупность значений неизвестных где i =1, 2, …, n, при подстановке которых уравнения системы обращаются в
- 4. Система, имеющая хоть одно решение, называется совместной. Система, не имеющая ни одного решения, называется несовместной. Система,
- 5. Правило Крамера решения систем линейных уравнений
- 6. Рассмотрим систему линейных уравнений Система трех уравнений может быть решена по правилу Крамера,
- 7. Составим определитель из коэффициентов при неизвестных Назовем его определителем системы. Если Δ≠0, то система совместна
- 8. Далее составим три вспомогательных определителя: , ,
- 9. Решение системы (10) находим по формулам: , , которые называют формулами Крамера
- 10. Замечание. Правило Крамера при n>3 не имеет практического применения из-за громоздкости вычислений.
- 11. Пример Решить систему уравнений
- 12. Решение систем линейных уравнений средствами матричного исчисления
- 13. Рассмотрим систему 3-х линейных уравнений с 3-мя неизвестными:
- 14. Составим из коэффициентов при неизвестных матрицу и назовем ее матрицей системы.
- 15. Матрицу называют матрицей-столбцом из свободных членов, а матрицу - матрицей-столбцом из неизвестных.
- 16. Запишем систему уравнений в виде матричного уравнения . Умножая обе части этого уравнения слева на ,
- 17. Таким образом, если матрица А системы невырожденная, т.е. существует , то решение системы линейных уравнений можно
- 18. Замечание Метод матричного исчисления обычно применяют для решения систем трех уравнений с тремя неизвестными. Решать этим
- 19. Пример Средствами матричного исчисления решить систему линейных уравнений
- 20. Ранг матрицы. Элементарные преобразования.
- 21. Миноры матрицы Рассмотрим матрицу А размера . Выберем в этой матрице произвольно k строк и k
- 22. Пример Из матрицы можно составить 12 миноров 1-го порядка – это сами элементы матрицы А.
- 23. Если выбрать какие-либо две строки и два столбца матрицы, то можно составить миноры 2-го порядка, например
- 24. Ранг матрицы Рангом матрицы называется наивысший из порядков отличных от нуля миноров матрицы. Ранг матрицы A
- 25. Элементарные преобразования матрицы Для вычисления ранга матрицы ее сначала приводят к более простому виду с помощью
- 26. 1.Умножение всех элементов строк на одно и то же число не равное 0. 2. Перестановка строк
- 27. 4.Отбрасывание одной из двух одинаковых строк. 5.Отбрасывание нулевой строки.
- 28. Теорема: Элементарные преобразования не меняют ранг матрицы. Матрицы, полученные с помощью элементарных преобразований, называют эквивалентными (~).
- 29. Если с помощью элементарных преобразований получить нули ниже главной диагонали матрицы, то ранг исходной матрицы будет
- 30. Пример С помощью элементарных преобразований вычислить ранг матрицы
- 31. Понятие о линейной зависимости Рассмотрим матрицу Обозначим ее строки Очевидно . Это равенство понимается в смысле
- 32. Строки матрицы А линейно зависимы, если можно подобрать такие не равные нулю одновременно числа , что
- 33. Если одна из строк матрицы линейно выражается через другие строки, то строки этой матрицы между собой
- 34. Пример Строки такой матрицы линейно независимы (лнз), так как их невозможно выразить одну через другую:
- 35. Теорема о ранге матрицы Ранг матрицы равен максимальному числу линейно – независимых строк матрицы.
- 36. Теорема. Если ранг матрицы равен r, то в этой матрице можно найти r линейно независимых строк
- 38. Скачать презентацию



































 Презентация "Луис Комфорт Тиффани" - скачать презентации по МХК
Презентация "Луис Комфорт Тиффани" - скачать презентации по МХК Тепловые машины и КПД
Тепловые машины и КПД  Последствия и значение ВГО
Последствия и значение ВГО Салфетки. Способы складывания салфеток
Салфетки. Способы складывания салфеток Украинская православная церковь
Украинская православная церковь Исследовательская и проектная деятельность школьников Круткова Светлана Анатольевна МОУ «Ашпанская ООШ»
Исследовательская и проектная деятельность школьников Круткова Светлана Анатольевна МОУ «Ашпанская ООШ» Возникновение ислама. Арабский халифат
Возникновение ислама. Арабский халифат Задания по курсу Теория организации и организационное поведение «Анализ деятельности региональной компании»
Задания по курсу Теория организации и организационное поведение «Анализ деятельности региональной компании»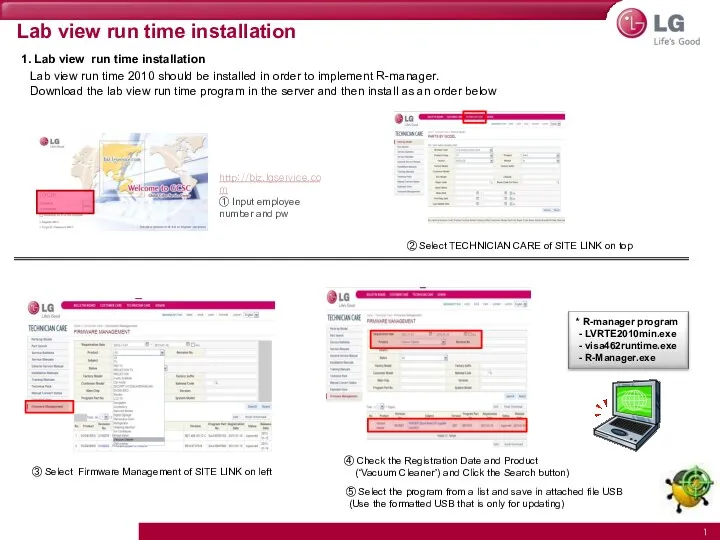 Lab view run time installation
Lab view run time installation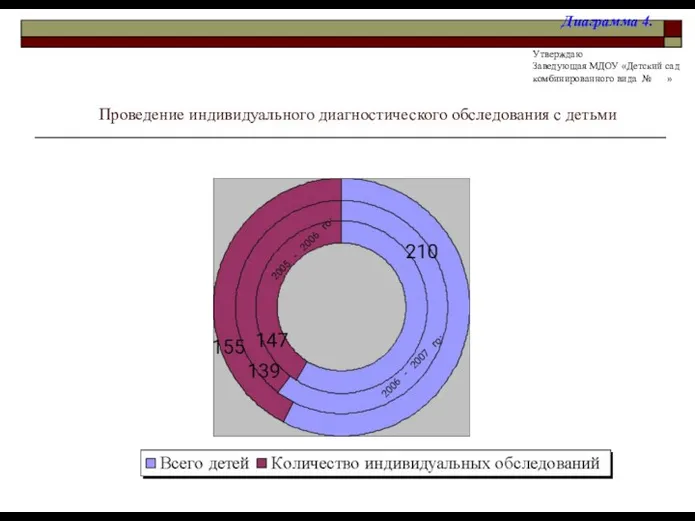 Проведение индивидуального диагностического обследования с детьми
Проведение индивидуального диагностического обследования с детьми  Настройка ПИД-регулятора
Настройка ПИД-регулятора Храм. Внешнее устройство
Храм. Внешнее устройство Христианская апологетика и история
Христианская апологетика и история Лептоспироз Выполнили: Попова Ксения, Столяр Елена, 2 курс фармацевтического факультета, 3 группа, 2011
Лептоспироз Выполнили: Попова Ксения, Столяр Елена, 2 курс фармацевтического факультета, 3 группа, 2011 Музеи, как рекреационные ресурсы познавательного мира
Музеи, как рекреационные ресурсы познавательного мира Develop a web application using the methods of expert analysis
Develop a web application using the methods of expert analysis Cities and attractions in the USA
Cities and attractions in the USA Виды рукавов в одежде
Виды рукавов в одежде Типы рыночных структур Проект по экономике для студентов 1 курса Авторы: Мельник Анастасия, Корякина Любовь
Типы рыночных структур Проект по экономике для студентов 1 курса Авторы: Мельник Анастасия, Корякина Любовь Врачебный контроль в физической культуре
Врачебный контроль в физической культуре Paris. La Capitale De La France
Paris. La Capitale De La France Instrumente und Applikationen WEB 2
Instrumente und Applikationen WEB 2 Алгоритмы и программирование, язык Паскаль (часть 3)
Алгоритмы и программирование, язык Паскаль (часть 3) Мембранная обработка молочного сырья
Мембранная обработка молочного сырья Казанский Базовый Медицинский Колледж ПРЕЗЕНТАЦИЯ Общение с больными на различных этапах медицинской службы. Выполнила
Казанский Базовый Медицинский Колледж ПРЕЗЕНТАЦИЯ Общение с больными на различных этапах медицинской службы. Выполнила Kinetika2
Kinetika2 Спортивная экипировка лыжника
Спортивная экипировка лыжника Простейший карбюратор
Простейший карбюратор