Содержание
- 2. 1. Эллипс и его каноническое уравнение.
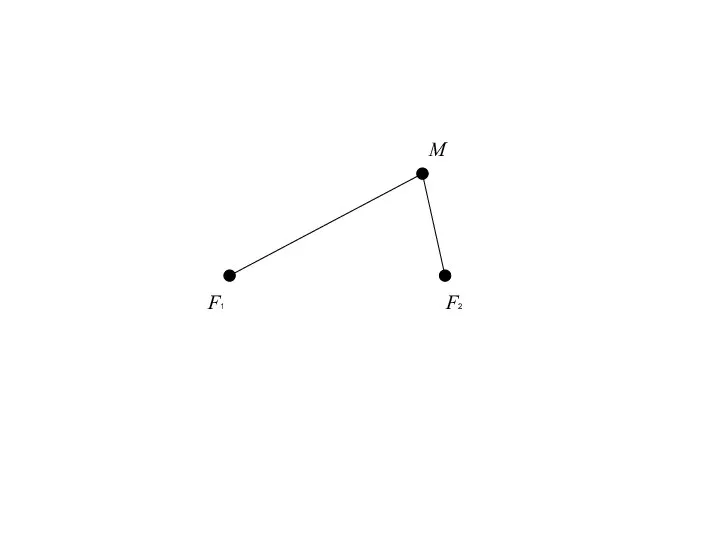
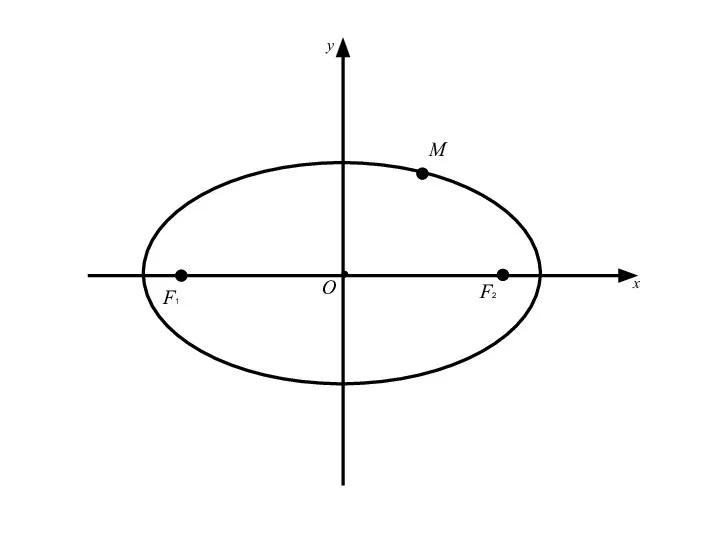
- 3. 1. Эллипс и его каноническое уравнение. Эллипсом называется геометрическое место точек плоскости, для каждой из которых
- 4. F1
- 5. F1 F2
- 6. F1 F2 M
- 7. F1 F2 M
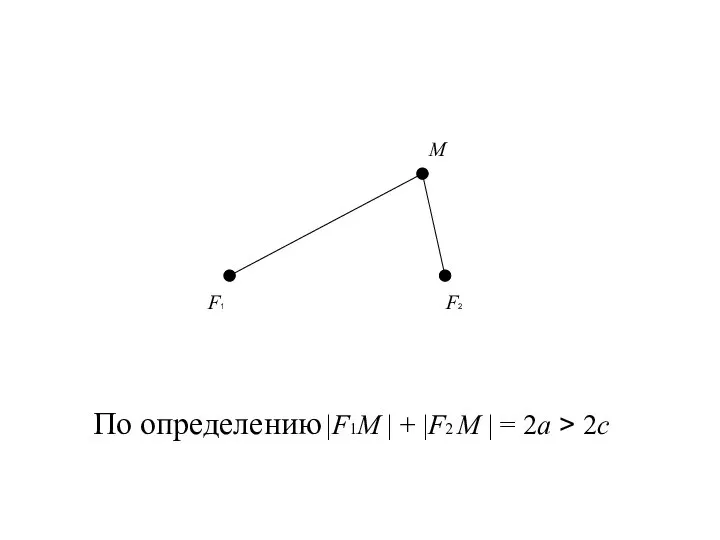
- 8. F1 F2 M По определению |F1М | + |F2 М | = 2a > 2c
- 9. F1 F2 M По определению |F1М | + |F2 М | = 2a > 2c |F1
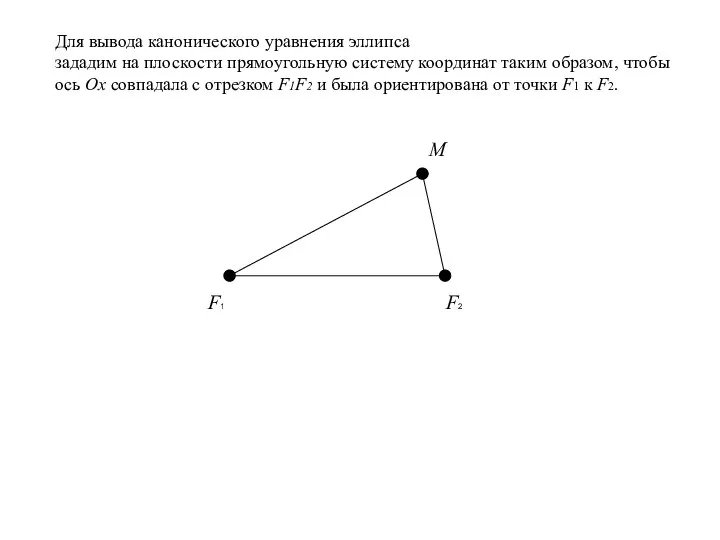
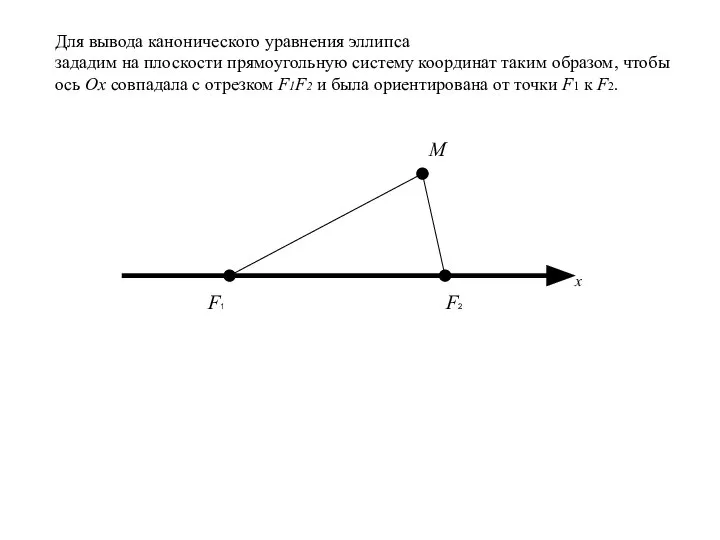
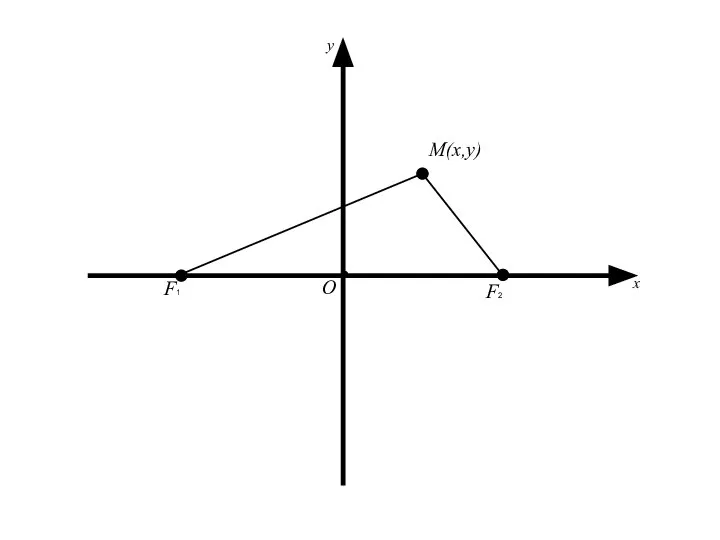
- 10. F1 F2 M Для вывода канонического уравнения эллипса зададим на плоскости прямоугольную систему координат таким образом,
- 11. F1 F2 M Для вывода канонического уравнения эллипса зададим на плоскости прямоугольную систему координат таким образом,
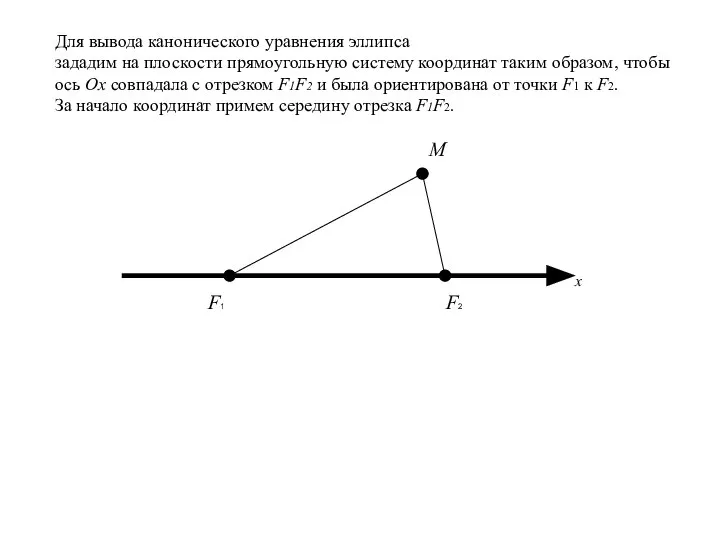
- 12. F1 F2 M Для вывода канонического уравнения эллипса зададим на плоскости прямоугольную систему координат таким образом,
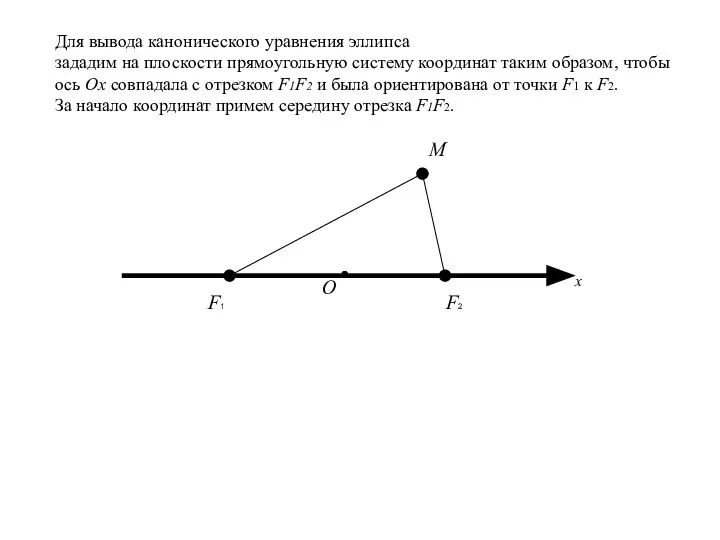
- 13. F1 F2 M О x Для вывода канонического уравнения эллипса зададим на плоскости прямоугольную систему координат
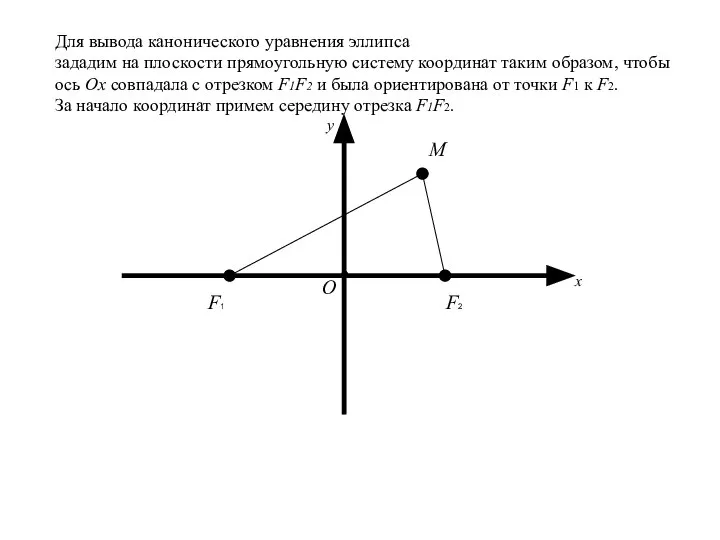
- 14. F1 F2 M О x y Для вывода канонического уравнения эллипса зададим на плоскости прямоугольную систему
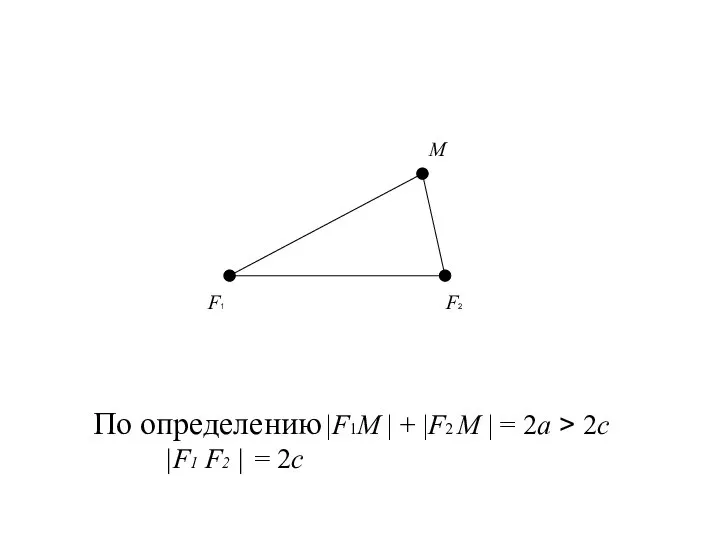
- 15. Так как |F1 F2 | = 2c,
- 16. Так как |F1 F2 | = 2c, значит в выбранной системе координат фокусы имеют координаты
- 17. Так как |F1 F2 | = 2c, значит в выбранной системе координат фокусы имеют координаты F1
- 18. Так как |F1 F2 | = 2c, значит в выбранной системе координат фокусы имеют координаты F1
- 19. Так как |F1 F2 | = 2c, значит в выбранной системе координат фокусы имеют координаты F1
- 20. По определению |F1М | + |F2 М | = 2a (1) Получим
- 21. По определению |F1М | + |F2 М | = 2a (1) Получим
- 24. Таким образом, мы доказали, что координаты любой точки M (x; y) эллипса удовлетворяют уравнению (2).
- 25. Таким образом, мы доказали, что координаты любой точки M (x; y) эллипса удовлетворяют уравнению (2). Однако
- 26. Если числа x и y удовлетворяют уравнению (2), то точка M (x; y) удовлетворяет соотношению (1),
- 27. Если числа x и y удовлетворяют уравнению (2), то точка M (x; y) удовлетворяет соотношению (1),
- 28. Докажем это утверждение Пусть точка M (x; y) удовлетворяет уравнению (2), тогда выразим :
- 32. Таким образом, уравнение (2) есть уравнение эллипса, т.к. доказано, что координаты любой точки M (x; y)
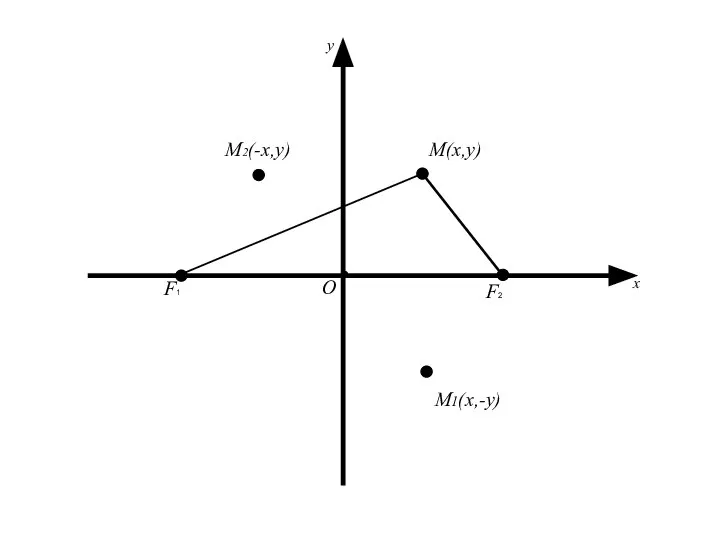
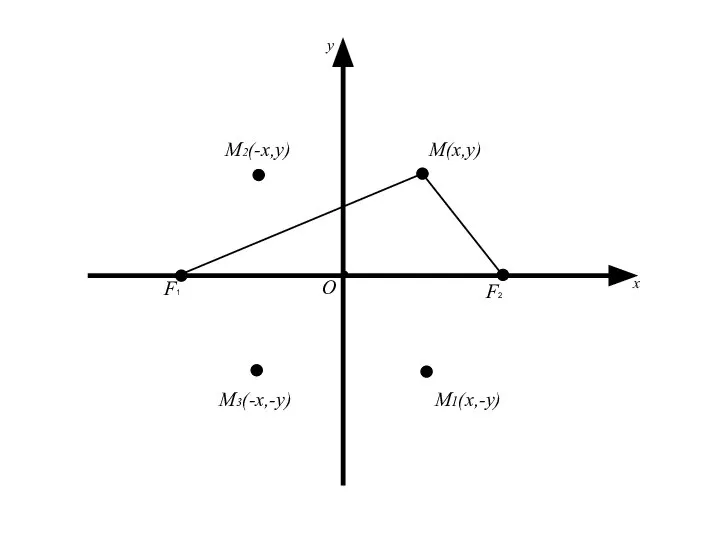
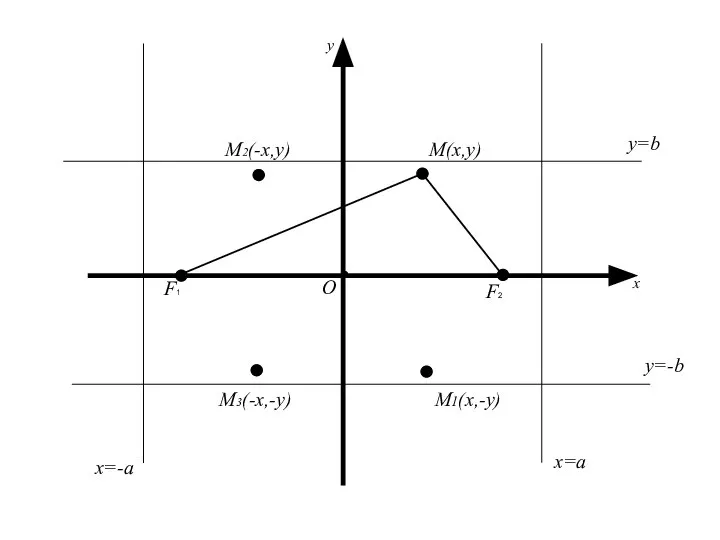
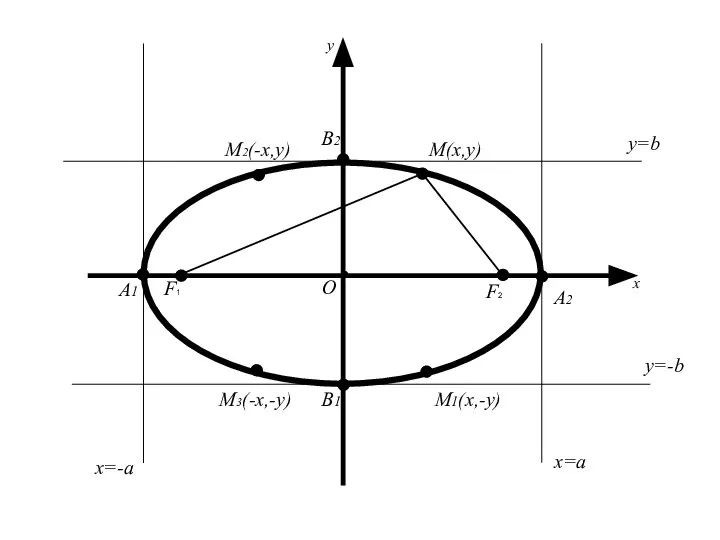
- 34. 2. Исследование формы эллипса. Так как координаты x и y входят в уравнение в четной степени,
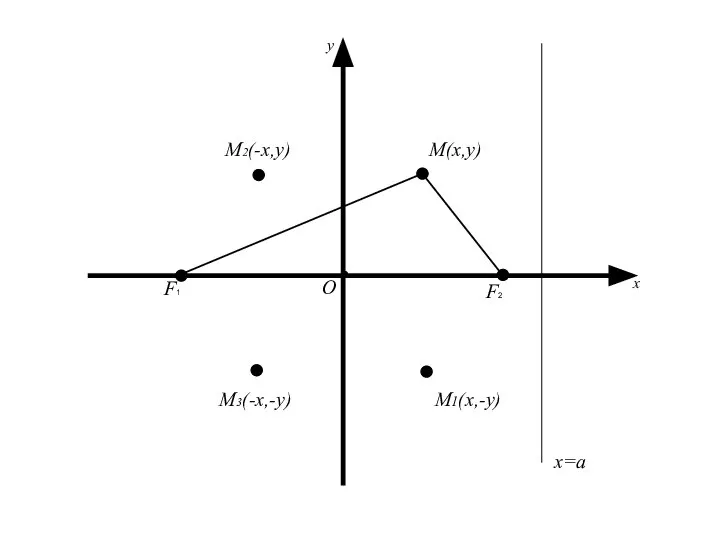
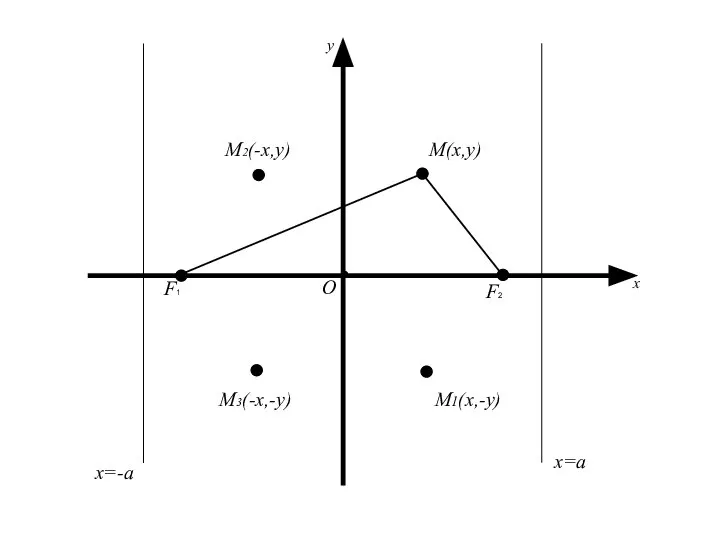
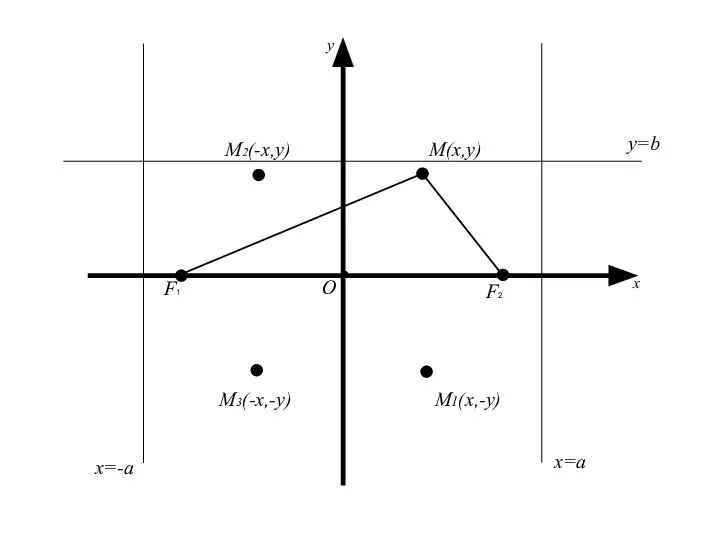
- 35. Следует, что для координат любой точки имеет место Геометрически это означает, что эллипс расположен внутри прямоугольника,
- 36. M(x,y) О x y F2 F1
- 37. M(x,y) О x y M1(x,-y) F2 F1
- 38. M(x,y) О x y M2(-x,y) M1(x,-y) F2 F1
- 39. M(x,y) О x y M2(-x,y) M3(-x,-y) M1(x,-y) F2 F1
- 40. M(x,y) О x y M2(-x,y) M3(-x,-y) M1(x,-y) x=a F2 F1
- 41. M(x,y) О x y M2(-x,y) M3(-x,-y) M1(x,-y) x=a x=-a F2 F1
- 42. M(x,y) О x y M2(-x,y) M3(-x,-y) M1(x,-y) x=a x=-a y=b F2 F1
- 43. M(x,y) О x y M2(-x,y) M3(-x,-y) M1(x,-y) x=a x=-a y=b y=-b F2 F1
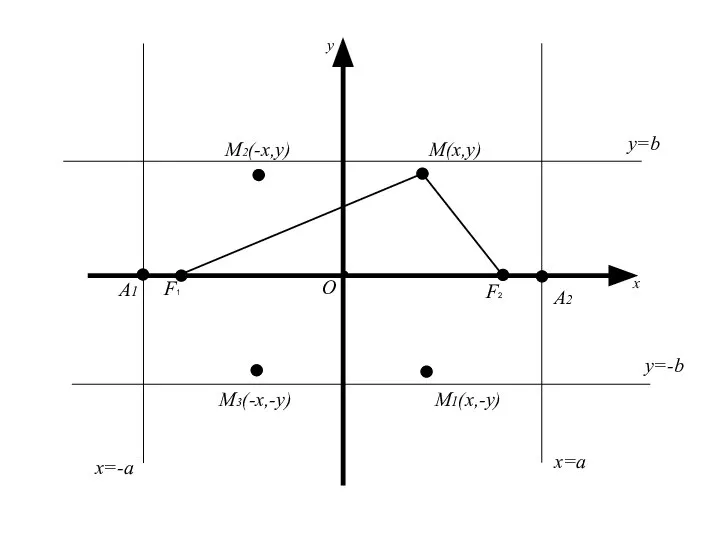
- 44. M(x,y) О x y M2(-x,y) M3(-x,-y) M1(x,-y) x=a x=-a y=b y=-b А1 F2 F1
- 45. M(x,y) О x y M2(-x,y) M3(-x,-y) M1(x,-y) x=a x=-a y=b y=-b А1 A2 F2 F1
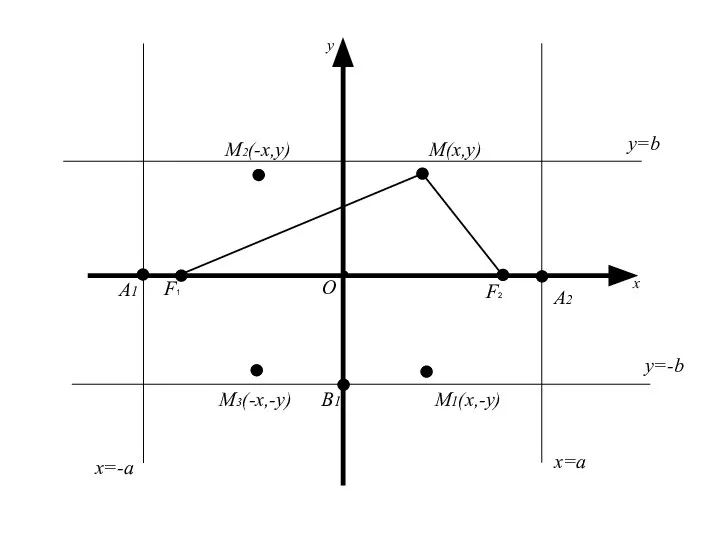
- 46. M(x,y) О x y M2(-x,y) M3(-x,-y) M1(x,-y) x=a x=-a y=b y=-b А1 B1 A2 F2 F1
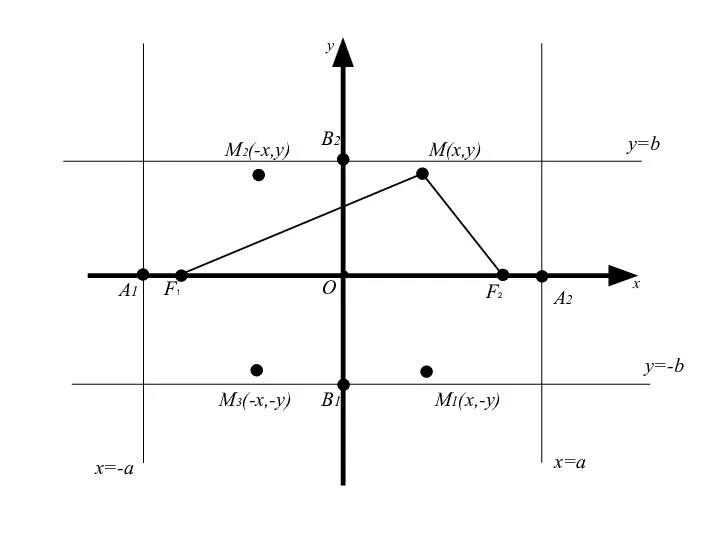
- 47. M(x,y) О x y M2(-x,y) M3(-x,-y) M1(x,-y) x=a x=-a y=b y=-b А1 B2 B1 A2 F2
- 48. F2 M(x,y) О x y M2(-x,y) M3(-x,-y) M1(x,-y) x=a x=-a y=b y=-b А1 B2 B1 A2
- 49. F2 M О x y А1 B2 B1 A2 F1
- 50. Точки пересечения эллипса с осями координат называются вершинами эллипса
- 51. Точки пересечения эллипса с осями координат называются вершинами эллипса Полуосью эллипса называется отрезок, одним концом которого
- 52. Точки пересечения эллипса с осями координат называются вершинами эллипса Полуосью эллипса называется отрезок, одним концом которого
- 53. Точки пересечения эллипса с осями координат называются вершинами эллипса Полуосью эллипса называется отрезок, одним концом которого
- 54. Отношение половины расстояния между фокусами эллипса (фокальное расстояние) к большей полуоси эллипса называется эксцентриситетом эллипса и
- 55. Отношение половины расстояния между фокусами эллипса (фокальное расстояние) к большей полуоси эллипса называется эксцентриситетом эллипса и
- 56. Отношение половины расстояния между фокусами эллипса (фокальное расстояние) к большей полуоси эллипса называется эксцентриситетом эллипса и
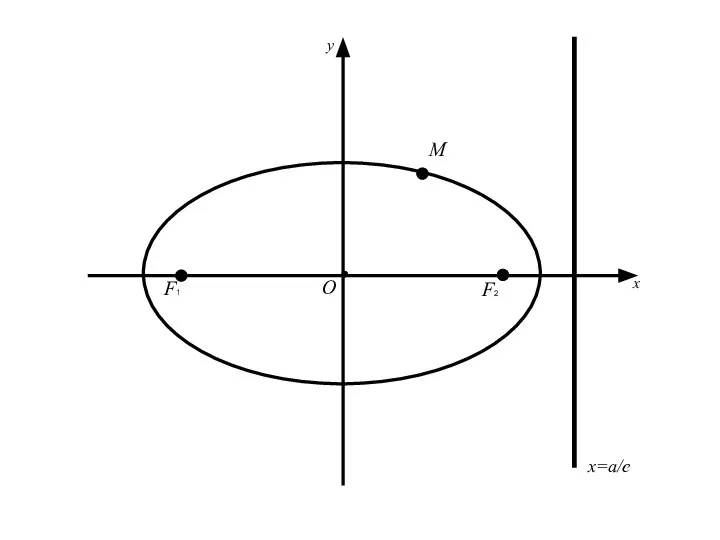
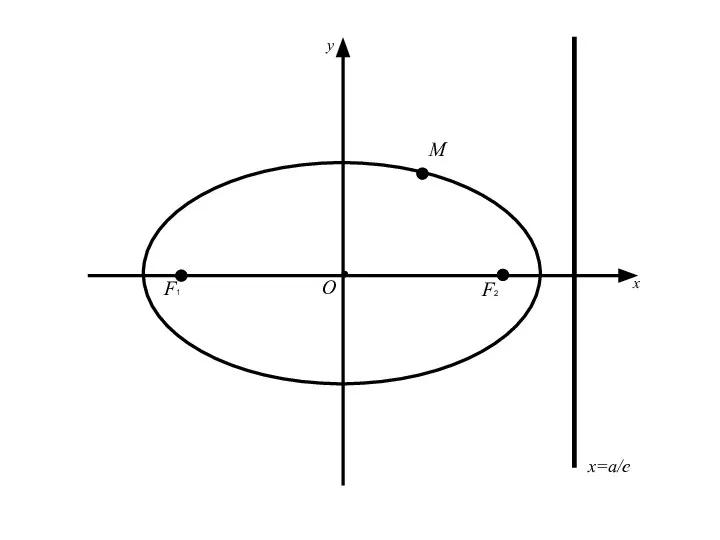
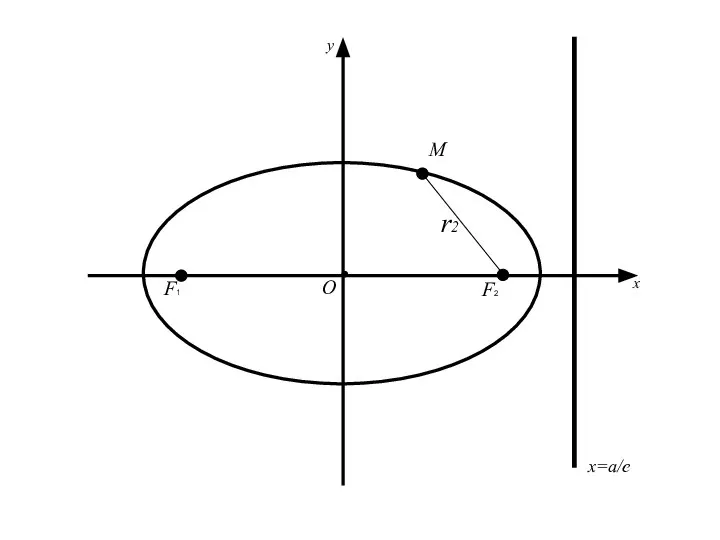
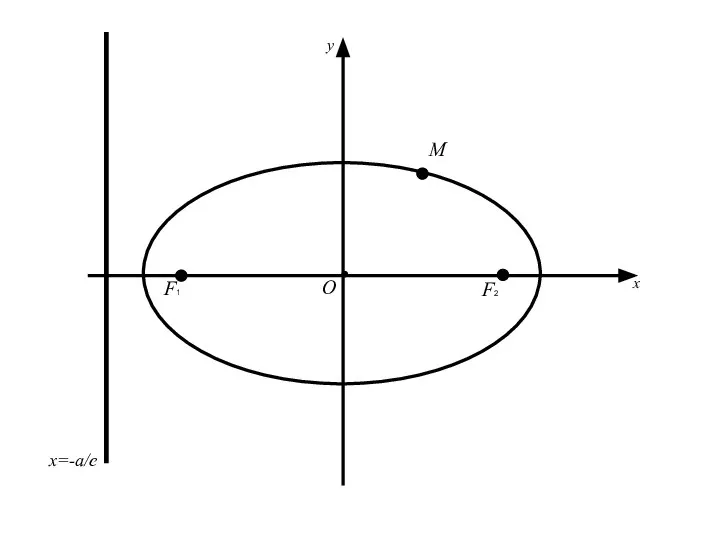
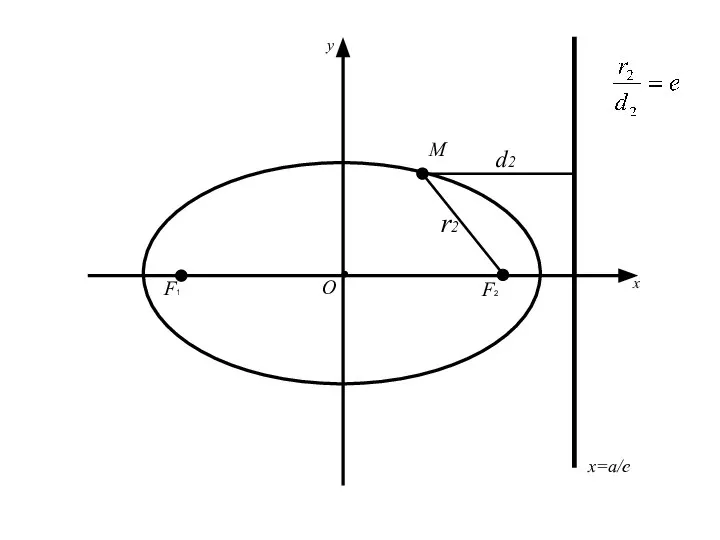
- 57. 3.Директрисы эллипса. Две прямые перпендикулярные оси эллипса, на которой расположены его фокусы, и отстоящие от центра
- 58. 3.Директрисы эллипса. Две прямые перпендикулярные оси эллипса, на которой расположены его фокусы, и отстоящие от центра
- 59. F1 F2 M О x y
- 60. F1 F2 M О x y x=a/e
- 61. F1 F2 M О x y x=a/e x=-a/e
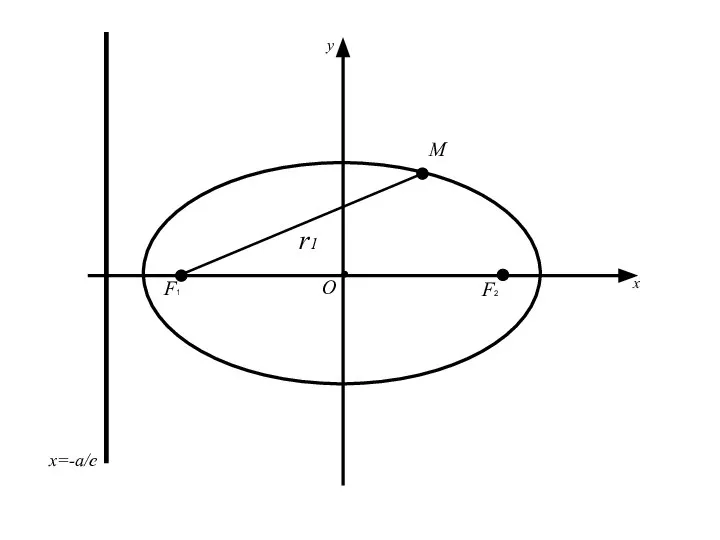
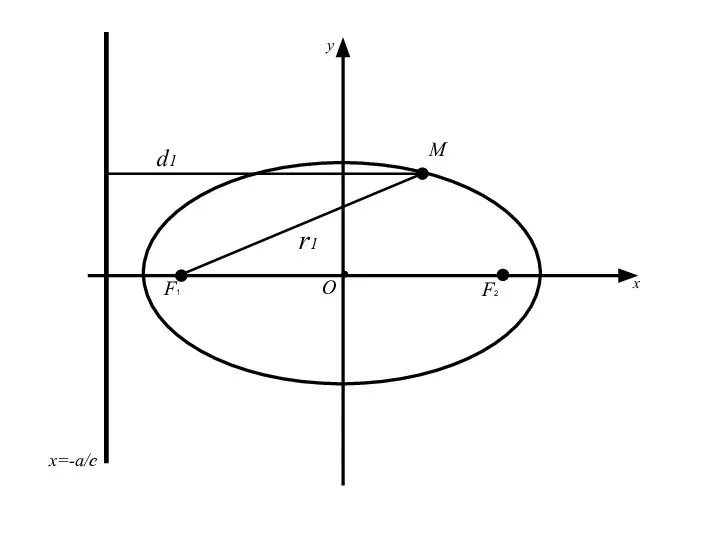
- 62. Теорема: Для того, чтобы точка лежала на эллипсе необходимо и достаточно, чтобы отношение расстояния от этой
- 63. F1 F2 M О x y x=a/e
- 64. F1 F2 M О x y x=a/e r2
- 65. F1 F2 M О x y x=a/e d2 r2
- 66. F1 F2 M О x y x=a/e d2 r2
- 67. F1 F2 M О x y x=-a/e
- 68. F1 F2 M О x y x=-a/e r1
- 69. F1 F2 M О x y x=-a/e d1 r1
- 70. F1 F2 M О x y x=-a/e d1 r1
- 71. F1 F2 M О x y x=a/e d2 r2
- 72. (=>) имеем точку M(x;y) принадлежащую эллипсу (2), для которой выполняется
- 73. (=>) имеем точку M(x;y) принадлежащую эллипсу (2), для которой выполняется
- 74. (=>) имеем точку M(x;y) принадлежащую эллипсу (2), для которой выполняется требуется доказать, что
- 75. (=>) имеем точку M(x;y) принадлежащую эллипсу (2), для которой выполняется требуется доказать, что найдём
- 76. (=>) имеем точку M(x;y) принадлежащую эллипсу (2), для которой выполняется требуется доказать, что найдём
- 77. (=>) имеем точку M(x;y) принадлежащую эллипсу (2), для которой выполняется требуется доказать, что найдём
- 78. (=>) имеем точку M(x;y) принадлежащую эллипсу (2), для которой выполняется требуется доказать, что найдём
- 79. (=>) имеем точку M(x;y) принадлежащую эллипсу (2), для которой выполняется требуется доказать, что найдём
- 80. Пусть существует точка M(x;y), для которой выполняется докажем, что точка принадлежит эллипсу, т.е. её координаты удовлетворяют
- 81. Пусть существует точка M(x;y), для которой выполняется докажем, что точка принадлежит эллипсу, т.е. её координаты удовлетворяют
- 82. Пусть существует точка M(x;y), для которой выполняется докажем, что точка принадлежит эллипсу, т.е. её координаты удовлетворяют
- 83. Пусть существует точка M(x;y), для которой выполняется докажем, что точка принадлежит эллипсу, т.е. её координаты удовлетворяют
- 84. Пусть существует точка M(x;y), для которой выполняется докажем, что точка принадлежит эллипсу, т.е. её координаты удовлетворяют
- 85. Пусть существует точка M(x;y), для которой выполняется докажем, что точка принадлежит эллипсу, т.е. её координаты удовлетворяют
- 87. Скачать презентацию





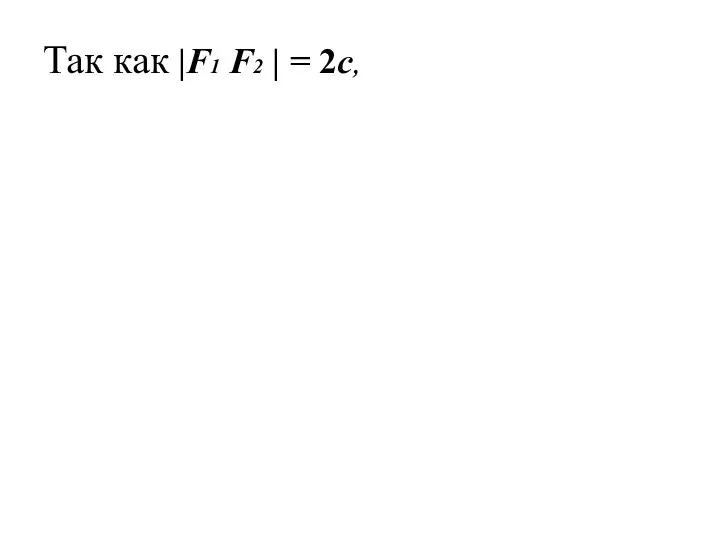

















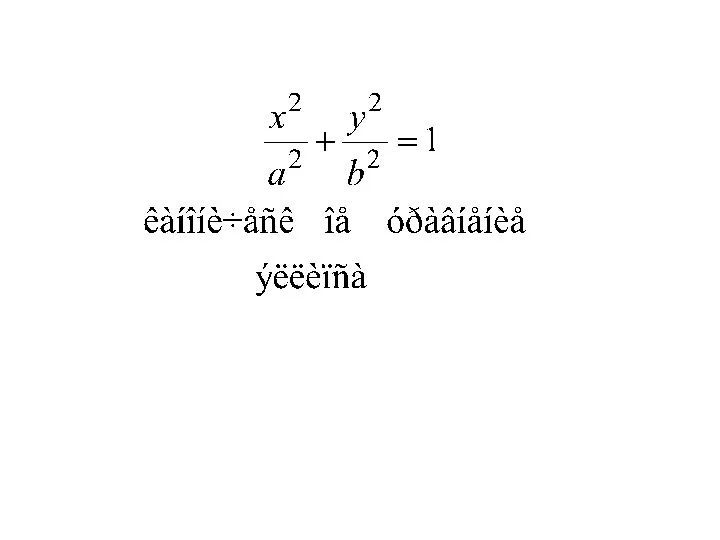

































 Кистевая роспись
Кистевая роспись  Педагогический_состав
Педагогический_состав Второй храм царя Давида и Соломона
Второй храм царя Давида и Соломона Специальное снаряжение для водного туризма
Специальное снаряжение для водного туризма Собственность членов фермерского хозяйства
Собственность членов фермерского хозяйства Судебное разбирательство и допрос потерпевших и свидетелей
Судебное разбирательство и допрос потерпевших и свидетелей Прибор для бесконтактного измерения удельного сопротивления полупроводниковых материалов
Прибор для бесконтактного измерения удельного сопротивления полупроводниковых материалов Воздействия на ландшафт
Воздействия на ландшафт Здание Сената и Синода
Здание Сената и Синода Архитектура младшей модели семейства Intel
Архитектура младшей модели семейства Intel О раздвоение личности одной знакомой Пушкина. Мадам Жорж – актриса или акушерка
О раздвоение личности одной знакомой Пушкина. Мадам Жорж – актриса или акушерка CrossFit. Программа Кроссфит
CrossFit. Программа Кроссфит Презентация на тему "Генная терапия" - скачать презентации по Медицине
Презентация на тему "Генная терапия" - скачать презентации по Медицине Святой пророк Илия
Святой пророк Илия Delphi программасымен жұмыс жасау ерекшелігі және оны пайдалану тәсілдері
Delphi программасымен жұмыс жасау ерекшелігі және оны пайдалану тәсілдері Loaders and ContentProviders
Loaders and ContentProviders Методы сбора и обработки данных при помощи Python
Методы сбора и обработки данных при помощи Python Бизнес-план обувного магазина «Юничел»
Бизнес-план обувного магазина «Юничел» Биохимия крови
Биохимия крови МФР в истории
МФР в истории  ВКР: Организация монтажа, технической эксплуатации и ремонта плоскошлифовального станка 3Е711В
ВКР: Организация монтажа, технической эксплуатации и ремонта плоскошлифовального станка 3Е711В Выпрямительные установки
Выпрямительные установки Дневники школьные
Дневники школьные Топография и геоматика
Топография и геоматика ЛЕКЦИЯ № 21 АВТОРСКИЕ СОВРЕМЕННЫЕ РОССИЙСКИЕ МОДИФИКАЦИИ
ЛЕКЦИЯ № 21 АВТОРСКИЕ СОВРЕМЕННЫЕ РОССИЙСКИЕ МОДИФИКАЦИИ Олимпийские сооружения Сочи 2014
Олимпийские сооружения Сочи 2014 ЧЕМ КОРМИТЬ ПТИЦ ЗИМОЙ? 1 КЛАСС
ЧЕМ КОРМИТЬ ПТИЦ ЗИМОЙ? 1 КЛАСС Однофазный АД
Однофазный АД