Содержание
- 2. 1. Интеграл Мора Используется в тех случаях, когда требуется найти перемещение в направлении не совпадающем с
- 3. Фиктивную силу Ф представляем в виде произведения скалярной величины Ф на единичный силовой фактор в соответствующем
- 4. - в случае крутящего момента. Определяем угол закручивания. MK1 – единичный крутящий момент приложенный в интересующей
- 5. После приложения фиктивной силы Ф значения силовых факторов в интересующем сечении будут равны сумме значений силовых
- 6. Дифференцируя по Ф, и принимая после этого Ф=0, находим перемещение. (формулы громоздкие, поэтому на примере одного
- 7. Суммируя все интегралы находим перемещение Формула носит название формула Мора, а входящие в формулу интегралы –
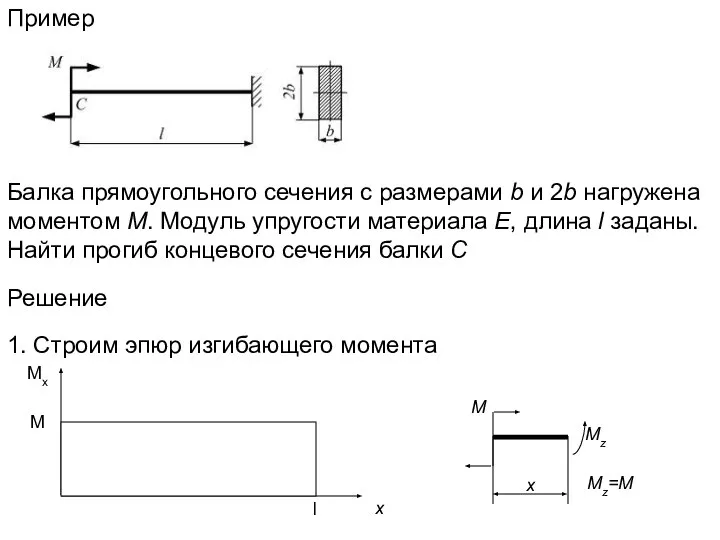
- 8. Пример Балка прямоугольного сечения с размерами b и 2b нагружена моментом М. Модуль упругости материала Е,
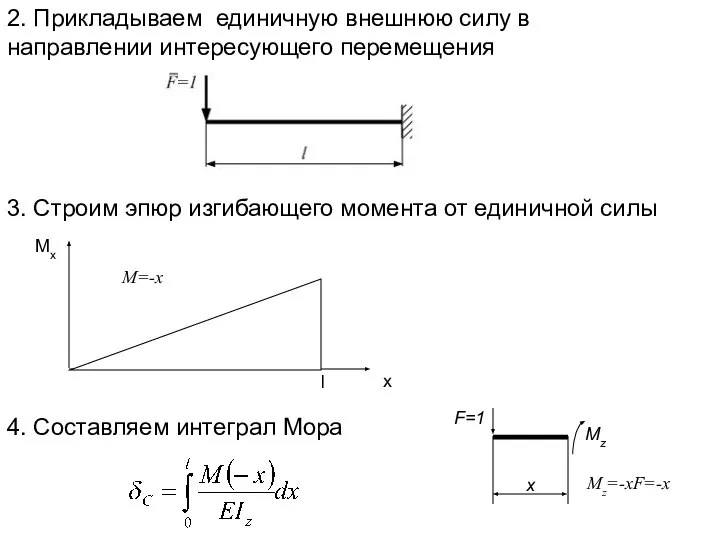
- 9. 2. Прикладываем единичную внешнюю силу в направлении интересующего перемещения 3. Строим эпюр изгибающего момента от единичной
- 10. 5. Вычисляем интеграл
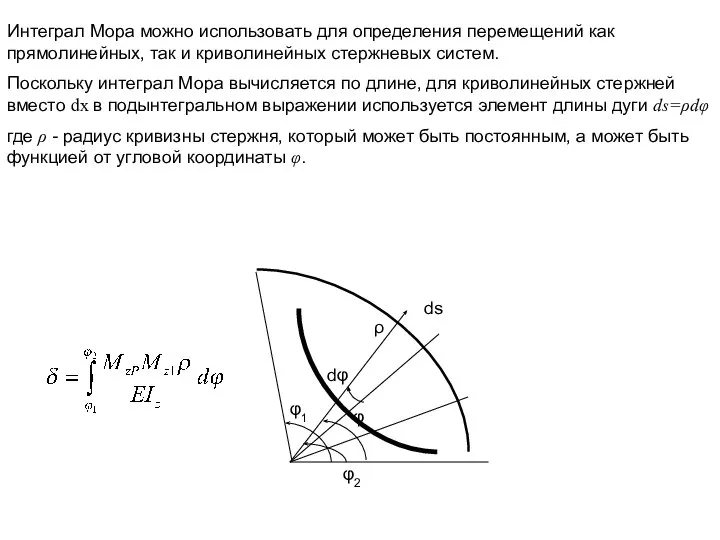
- 11. Интеграл Мора можно использовать для определения перемещений как прямолинейных, так и криволинейных стержневых систем. Поскольку интеграл
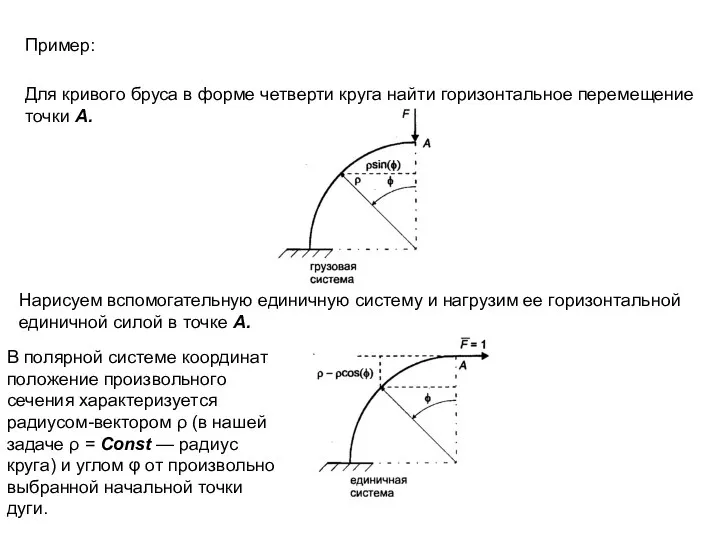
- 12. Пример: Для кривого бруса в форме четверти круга найти горизонтальное перемещение точки А. Нарисуем вспомогательную единичную
- 13. Изгибающий момент от внешних сил Изгибающий момент от единичной силы Горизонтальное перемещение точки А
- 14. Правило Верещагина Правило Верещагина – графо-аналитический метод, позволяющий упростить вычисления интегралов, входящих в формулу Мора. Упрощение
- 15. По свойству статического момента В сумме получаем Выражение в скобках – значение функции f2 под центром
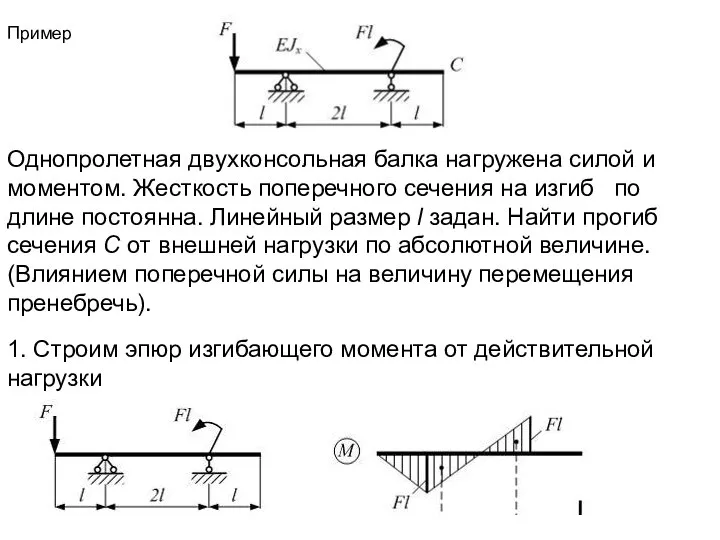
- 16. Пример Однопролетная двухконсольная балка нагружена силой и моментом. Жесткость поперечного сечения на изгиб по длине постоянна.
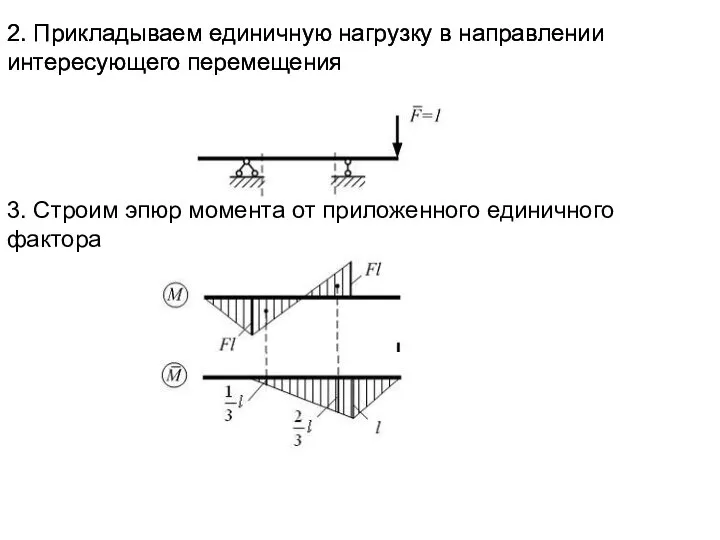
- 17. 2. Прикладываем единичную нагрузку в направлении интересующего перемещения 2. Прикладываем единичную нагрузку в направлении интересующего перемещения
- 18. 4. Находим интеграл Мора по правилу Верещагина
- 19. 3. Формула Мора для определения температурных перемещений сечения по заданному направлению В основу вывода формулы положен
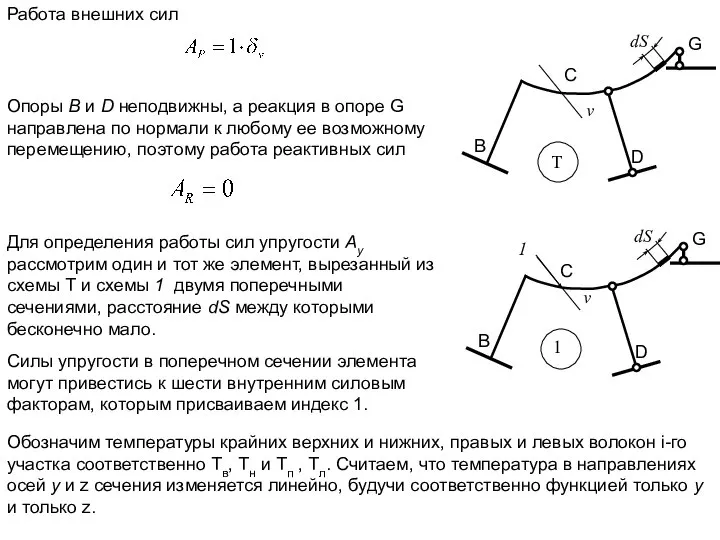
- 20. Работа внешних сил Опоры В и D неподвижны, а реакция в опоре G направлена по нормали
- 21. Законы изменения температуры по поперечному сечению показаны на рис. Очевидно, что Температура на оси элемента или
- 22. По аналогии, возможный относительный поворот концевых сечений элемента вокруг оси y где - наибольший размер поперечного
- 24. Скачать презентацию














 Міжнародні конфлікти
Міжнародні конфлікти Дополнительные устройства в микроконтроллере
Дополнительные устройства в микроконтроллере  Презентация по алгебре Решение уравнений,содержащих переменную под знаком модуля
Презентация по алгебре Решение уравнений,содержащих переменную под знаком модуля  Презентация Требования, предъявляемые к мировым ценам.
Презентация Требования, предъявляемые к мировым ценам. Презентация "Управление финансовой деятельностью фитнес-клуба" - скачать презентации по Экономике
Презентация "Управление финансовой деятельностью фитнес-клуба" - скачать презентации по Экономике Достопримечательности г. Воткинска
Достопримечательности г. Воткинска Причины коррупции в сфере государственной службы
Причины коррупции в сфере государственной службы Презентация Понятие и назначение уголовного процесса.
Презентация Понятие и назначение уголовного процесса. Лекция 4. Генетика бактерий
Лекция 4. Генетика бактерий Бизнес план как базовый документ Стартапа Бизнес модель. Основные блоки
Бизнес план как базовый документ Стартапа Бизнес модель. Основные блоки  Урок математики в 1 классе по теме «Число 0. Его получение и обозначение» Составила: учитель начальных классов, МОУ СОШ м-на Вы
Урок математики в 1 классе по теме «Число 0. Его получение и обозначение» Составила: учитель начальных классов, МОУ СОШ м-на Вы Возрождение народного декоративно- прикладного искусства. Орнамент.
Возрождение народного декоративно- прикладного искусства. Орнамент. производство стеклотары
производство стеклотары  Профессионально – прикладная физическая культура
Профессионально – прикладная физическая культура Сущность и задачи финансового менеджмента
Сущность и задачи финансового менеджмента  Основы электричества и электротехники. Часть I
Основы электричества и электротехники. Часть I Презентация опыта работы учителя начальных классов МОУ СОШ № 6 п. Каскадный Андроповского района Ставропольского края по теме: «И
Презентация опыта работы учителя начальных классов МОУ СОШ № 6 п. Каскадный Андроповского района Ставропольского края по теме: «И СЕРТИФИКАЦИЯ И СИСТЕМЫ АККРЕДИТАЦИИ
СЕРТИФИКАЦИЯ И СИСТЕМЫ АККРЕДИТАЦИИ  Статистика таможенных правонарушений Выполнил: студентка 4 го курса ФТД группа Т-083 Бреус Я.Ю
Статистика таможенных правонарушений Выполнил: студентка 4 го курса ФТД группа Т-083 Бреус Я.Ю  Семь чудес Усть - Усы Семяшкина Александра Григорьевна - учитель технологии МОУ «СОШ» с.Усть-Уса
Семь чудес Усть - Усы Семяшкина Александра Григорьевна - учитель технологии МОУ «СОШ» с.Усть-Уса Белая рубашка
Белая рубашка Ситуация социализации как дидактическая единица обучения и воспитания Кочнева М.М. руководитель проблемной группы МОУ «СОШ №12»
Ситуация социализации как дидактическая единица обучения и воспитания Кочнева М.М. руководитель проблемной группы МОУ «СОШ №12» Презентация Служебное время и должностной регламент сотрудников таможенных органов
Презентация Служебное время и должностной регламент сотрудников таможенных органов Государственный долг внешний и внутренний Бурсаковский Сергей Т093
Государственный долг внешний и внутренний Бурсаковский Сергей Т093  Методы верификации прогнозных моделей
Методы верификации прогнозных моделей Nike компаниясы
Nike компаниясы Правила БПФ. Роли спикеров. Типы тем
Правила БПФ. Роли спикеров. Типы тем Язык программирования C#
Язык программирования C#