Содержание
- 2. Колебания и волны. Геометрическая и волновая оптика *
- 3. Кузнецов Сергей Иванович доцент кафедры общей физики ТПУ Ф И З И К А Часть 3
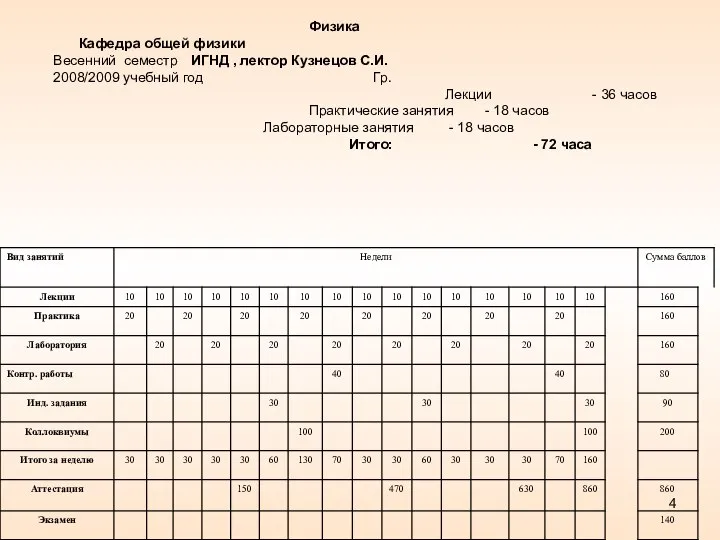
- 4. Физика Кафедра общей физики Весенний семестр ИГНД , лектор Кузнецов С.И. 2008/2009 учебный год Гр. Лекции
- 5. Литература 1. Ю.И. Тюрин, И.П. Чернов, Ю.Ю. Крючков ФИЗИКА, Ч.3. Оптика. Квантовая физика. 2. И.В. Савельев,
- 6. Раздел V Колебания и волны
- 7. Тема 1 ГАРМОНИЧЕСКИЕ КОЛЕБАНИЯ 1.1 Виды и признаки колебаний 1.2 Параметры гармонических колебаний 1.3 Графики смещения
- 8. Примеры колебательных процессов Круговая волна на поверхности жидкости, возбуждаемая точечным источником (гармонически колеблющимся шариком). Генерация акустической
- 9. Возможные типы колебаний атомов в кристалле. Поперечная волна в сетке, состоящей из шариков, скреплённых пружинками. Колебания
- 10. 1.1 Виды и признаки колебаний В физике особенно выделяют колебания двух видов – механические и электромагнитные
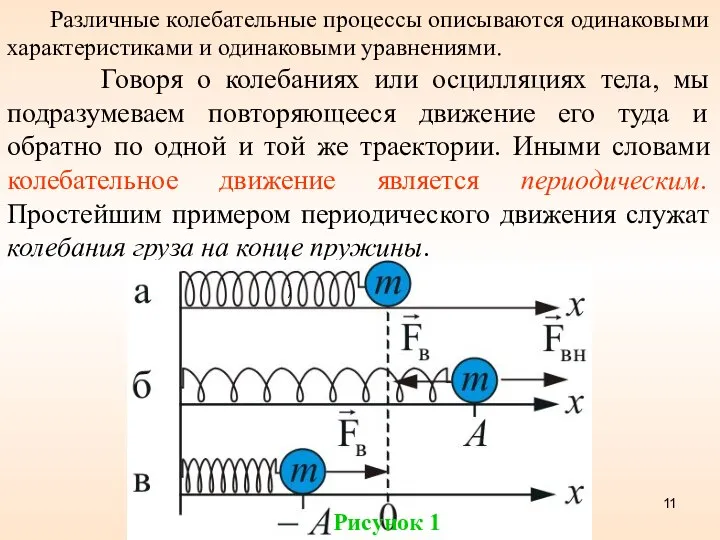
- 11. Различные колебательные процессы описываются одинаковыми характеристиками и одинаковыми уравнениями. Говоря о колебаниях или осцилляциях тела, мы
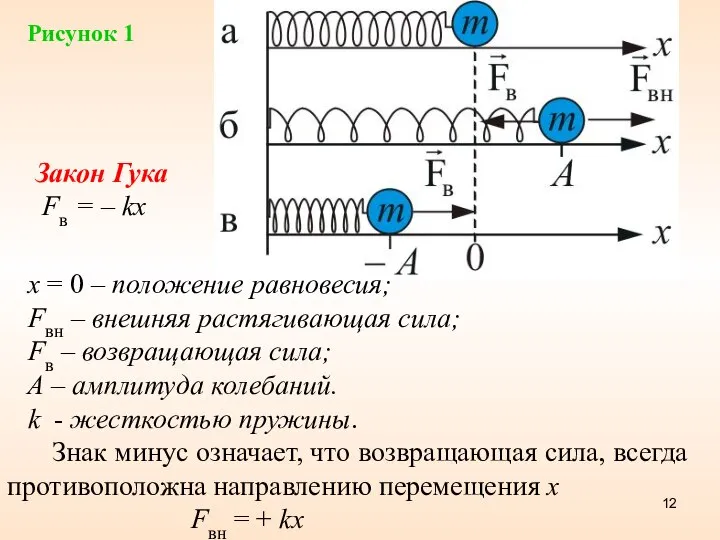
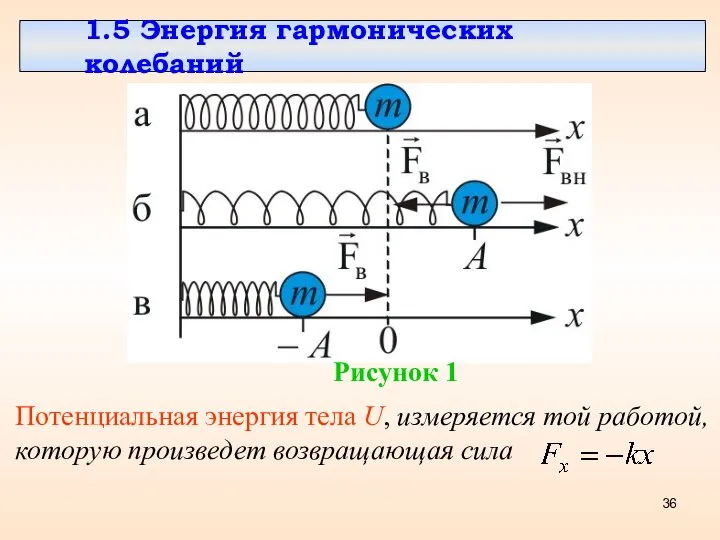
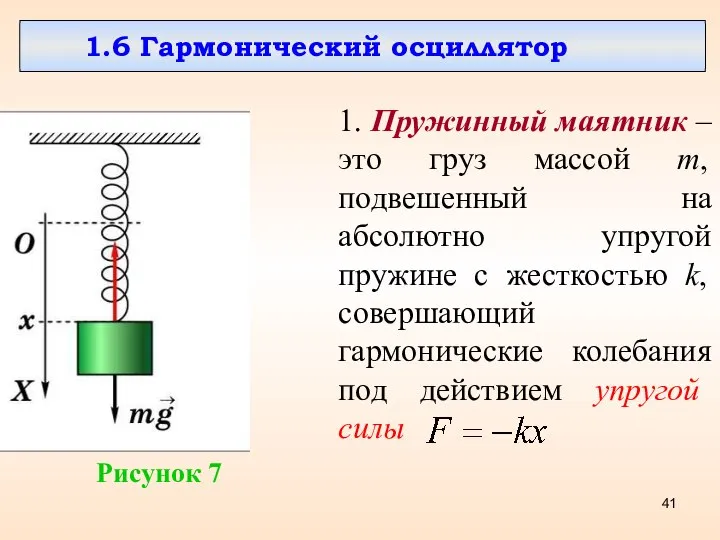
- 12. Рисунок 1 x = 0 – положение равновесия; Fвн – внешняя растягивающая сила; Fв – возвращающая
- 13. Из приведенного примера следуют три признака колебательного движения: повторяемость (периодичность) – движение по одной и той
- 14. Примеры колебательных процессов Опыт Кавендиша
- 15. Примеры колебательных процессов В случае абсолютно упругого столкновения шаров (нет потерь энергии) скорость и угол отклонения
- 16. Примеры колебательных процессов Упругое столкновение некоторого тела с баллистическим маятником: при движении маятника его продольная ось
- 17. Примеры колебательных процессов Столкновение абсолютно упругого шара с пружинным осциллятором. Со временем колебания затухают, часть энергии
- 19. Колебания называются периодическими, если значения физических величин, изменяющихся в процессе колебаний, повторяются через равные промежутки времени.
- 20. колебания, встречающиеся в природе и технике, часто имеют характер, близкий к гармоническому; различные периодические процессы (повторяющиеся
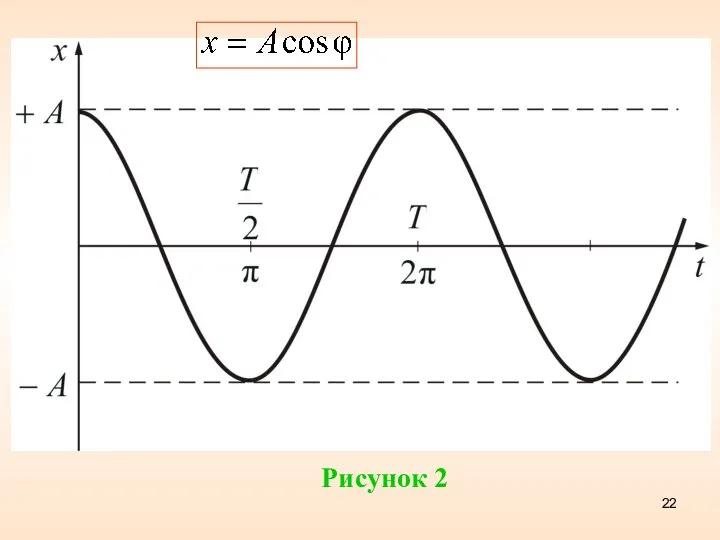
- 21. Расстояние груза от положения равновесия до точки, в которой находится груз, называют смещением x. Максимальное смещение
- 22. Рисунок 2
- 25. Движение от некоторой начальной точки до возвращения в ту же точку, например от к и обратно
- 26. ω – циклическая (круговая) частота – число полных колебаний за 2π секунд. Фаза φ не влияет
- 27. – амплитуда скорости; – амплитуда ускорения. Смещение описывается уравнением тогда, по определению: (1.2.4) (1.2.5) скорость ускорение
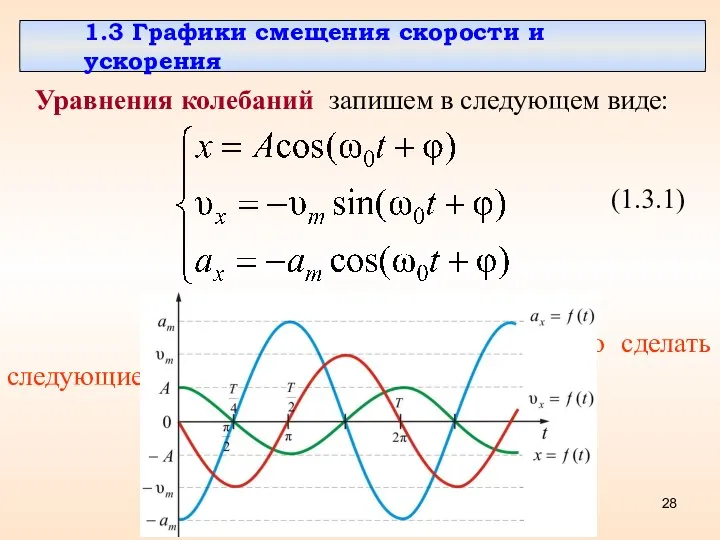
- 28. 1.3 Графики смещения скорости и ускорения Уравнения колебаний запишем в следующем виде: Из этой системы уравнений
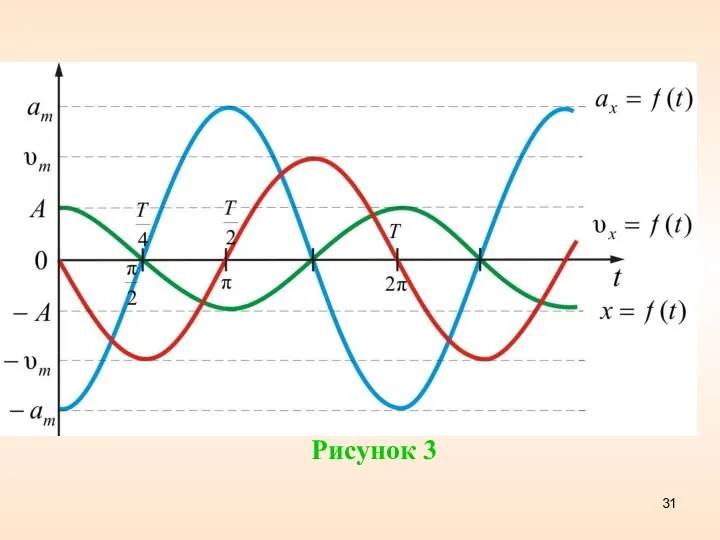
- 30. скорость колебаний тела максимальна и равна амплитуде скорости в момент прохождения через положение равновесия ( ).
- 31. Рисунок 3
- 32. Найдем разность фаз Δφ между фазами смещения х и скорости υx. то есть скорость опережает смещение
- 33. 1.4 Основное уравнение динамики гармонических колебаний Исходя из второго закона, , можно записать сила F пропорциональна
- 34. Сравнивая (1.4.1) и (1.4.2) видим, что Получим основное уравнение динамики гармонических колебаний, вызываемых упругими силами: или
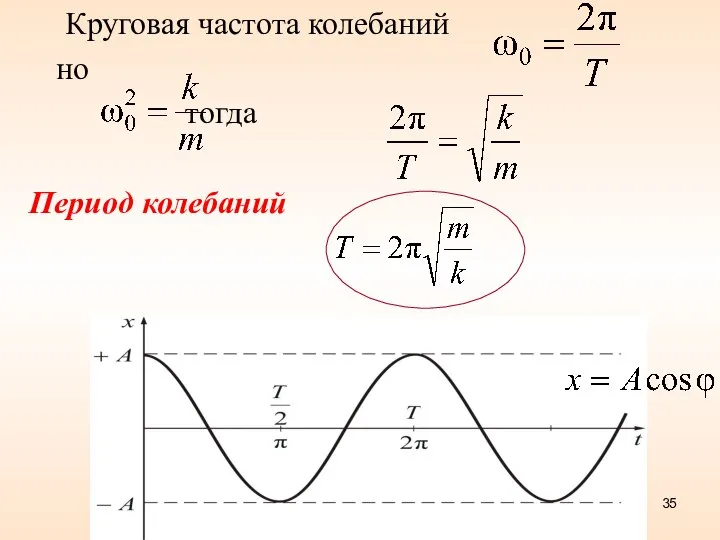
- 35. Круговая частота колебаний но тогда Период колебаний
- 36. 1.5 Энергия гармонических колебаний Рисунок 1 Потенциальная энергия тела U, измеряется той работой, которую произведет возвращающая
- 37. , отсюда или (1.5.1) (1.5.2) Кинетическая энергия (1.5.3) Полная энергия: , или Полная механическая энергия гармонически
- 38. Колебания груза под действием сил тяжести Максимум потенциальной энергии, (из 1.5.1) Максимум кинетической энергии но когда
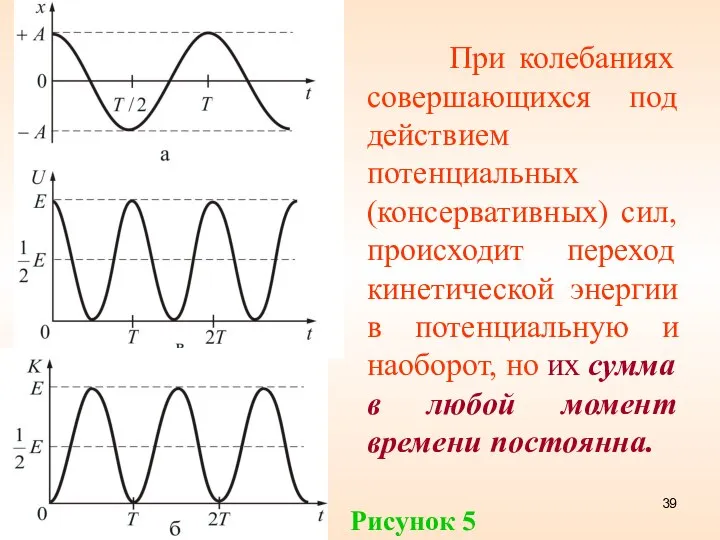
- 39. При колебаниях совершающихся под действием потенциальных (консервативных) сил, происходит переход кинетической энергии в потенциальную и наоборот,
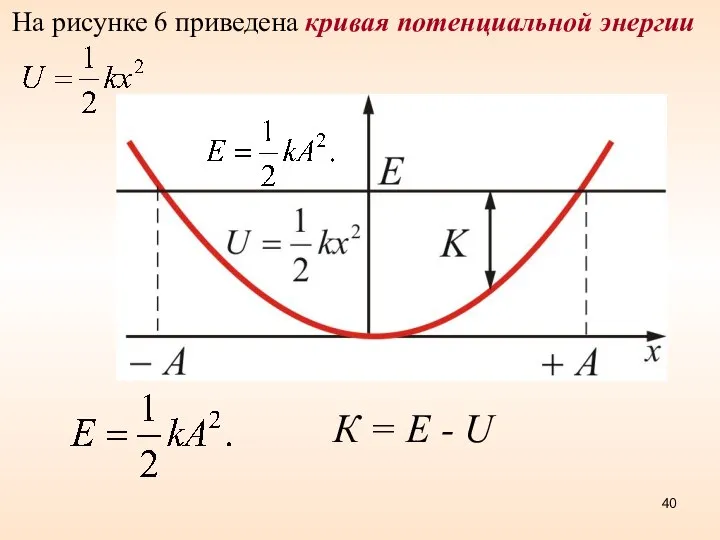
- 40. На рисунке 6 приведена кривая потенциальной энергии Рисунок 6 К = Е - U
- 41. 1.6 Гармонический осциллятор 1. Пружинный маятник – это груз массой m, подвешенный на абсолютно упругой пружине
- 42. или циклическая частота ω период Т Из второго закона Ньютона F = mа; или F =
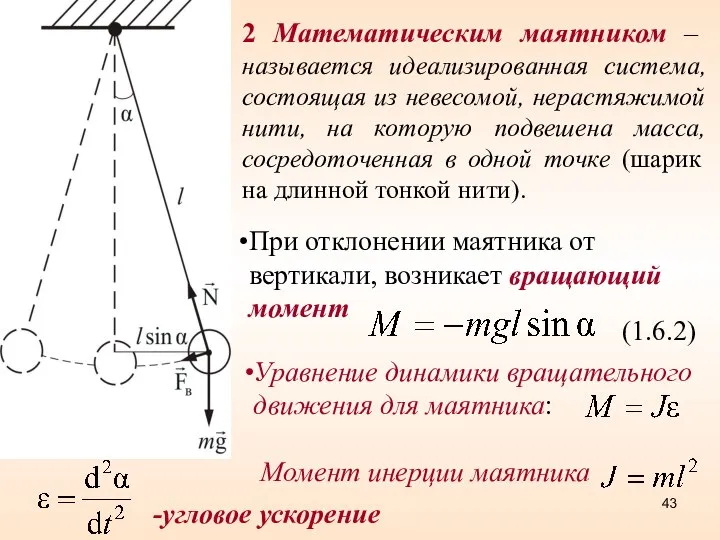
- 43. 2 Математическим маятником – называется идеализированная система, состоящая из невесомой, нерастяжимой нити, на которую подвешена масса,
- 44. Тогда , или Обозначим : (1.6.3) - Это уравнение динамики гармонических колебаний. Решение уравнения (1.5.3) имеет
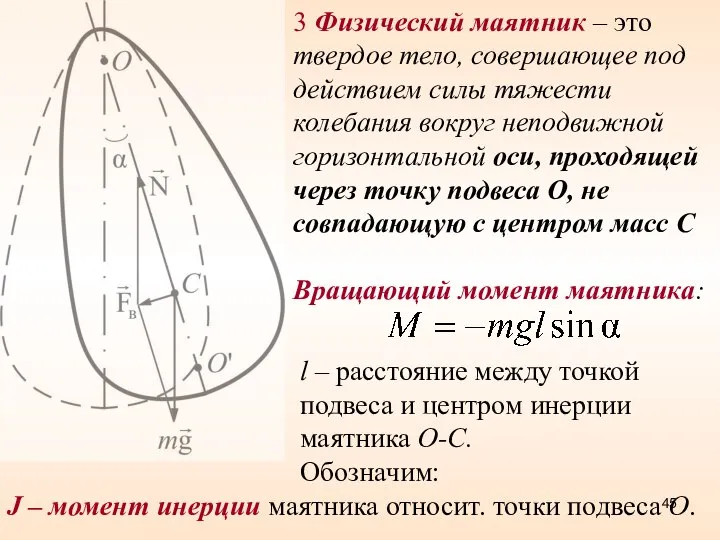
- 45. 3 Физический маятник – это твердое тело, совершающее под действием силы тяжести колебания вокруг неподвижной горизонтальной
- 46. - угловое ускорение, тогда Уравнение динамики вращательного движения где – приведенная длина физического маятника – это
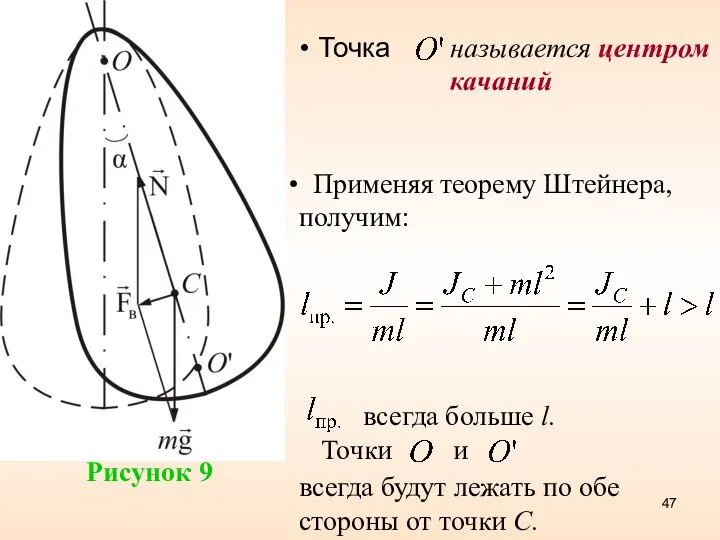
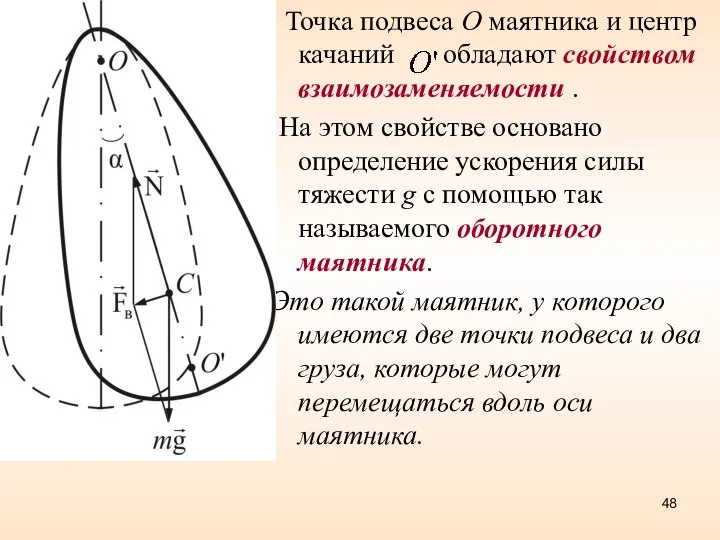
- 47. Точка называется центром качаний всегда больше l. Точки и всегда будут лежать по обе стороны от
- 48. Точка подвеса О маятника и центр качаний обладают свойством взаимозаменяемости . На этом свойстве основано определение
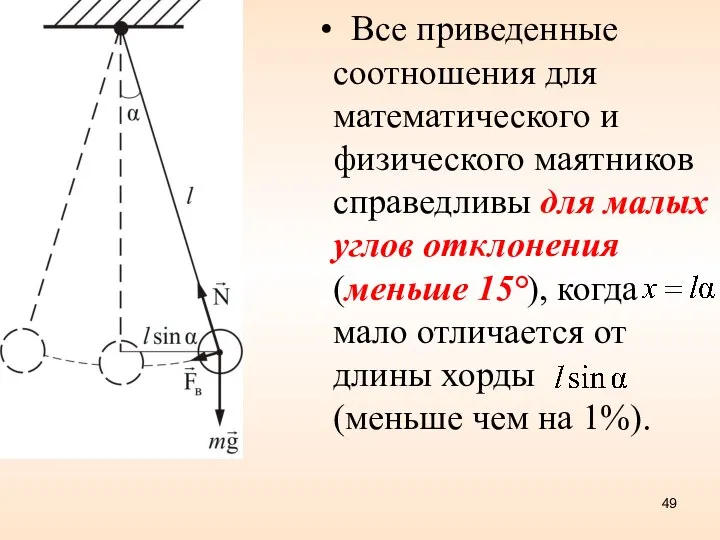
- 49. Все приведенные соотношения для математического и физического маятников справедливы для малых углов отклонения (меньше 15°), когда
- 50. Бенджамин Франклин за стеклянной гармоникой Его знаменитая гармоника была создана в 1763 году, а затем в
- 51. Визуализация узловых меридианов
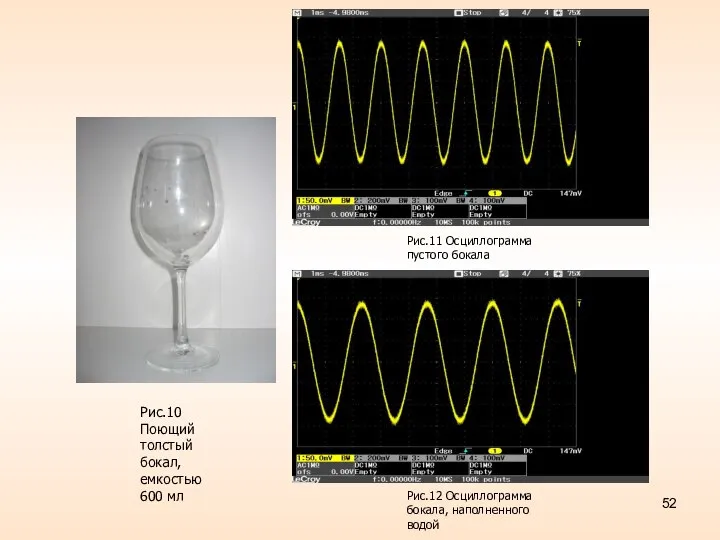
- 52. Рис.10 Поющий толстый бокал, емкостью 600 мл Рис.11 Осциллограмма пустого бокала Рис.12 Осциллограмма бокала, наполненного водой
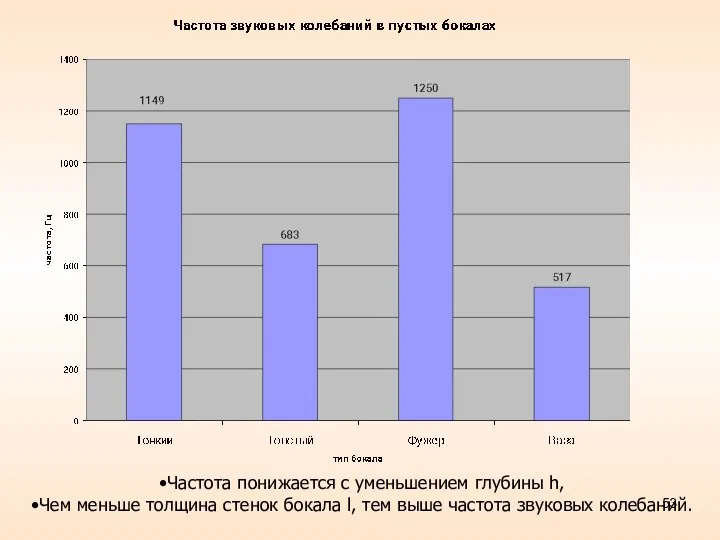
- 53. Частота понижается с уменьшением глубины h, Чем меньше толщина стенок бокала l, тем выше частота звуковых
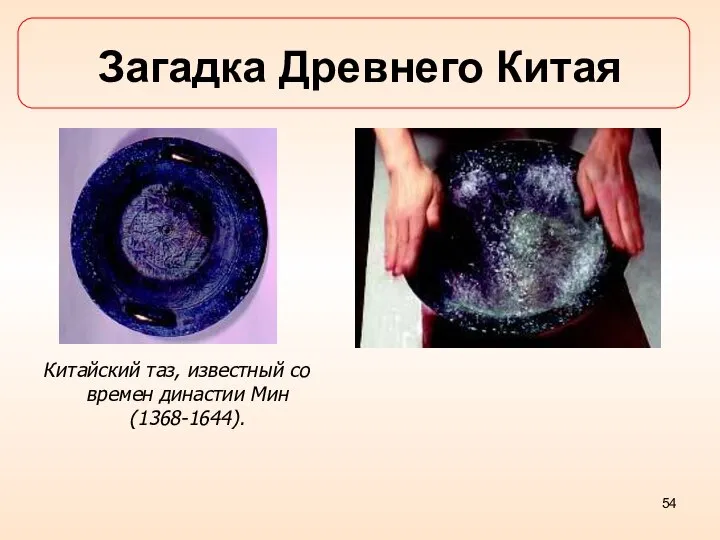
- 54. Загадка Древнего Китая Китайский таз, известный со времен династии Мин (1368-1644).
- 55. Комплексная форма представления гармонических колебаний Уравнение гармонических колебаний Сделаем замену: x = eλt Продифференцировав, получаем: Уравнение
- 56. Корни характеристического уравнения – мнимые: λ = ± iω0 Общее решение однородного ДУ В силу вещественности
- 57. Представим их в комплексной форме Z = ρeiφ, где в качестве модуля выбрано значение А/2: Тогда
- 58. Получаем выражение для гармонических функций: И выражение для функции х приобретает вид - гармоническое колебание. Из
- 60. Скачать презентацию




































 Процес формування та функціонування облікових підрозділів
Процес формування та функціонування облікових підрозділів Индейцы Америки
Индейцы Америки История развития языков и диалектов
История развития языков и диалектов Метод расчета конструкций по предельным состояниям
Метод расчета конструкций по предельным состояниям Генерация и оптимизация кода
Генерация и оптимизация кода Установка электромагнитного замка в модели L12 и L7
Установка электромагнитного замка в модели L12 и L7 Презентация
Презентация Информационное взаимодействие внутри профсоюзных структур Комагорова Мария первый заместитель главного редактора газеты «С
Информационное взаимодействие внутри профсоюзных структур Комагорова Мария первый заместитель главного редактора газеты «С dg4hRLlQZepeS_oM1Vq7vA
dg4hRLlQZepeS_oM1Vq7vA Алгоритмы траекторной обработки данных
Алгоритмы траекторной обработки данных Международный терроризм как глобальная геополитическая проблема
Международный терроризм как глобальная геополитическая проблема Современные переводы Библии
Современные переводы Библии Laxus minimal
Laxus minimal Травма челюстей 2015
Травма челюстей 2015 Цифровая схемотехника. Цифровые автоматы Мили и Мура
Цифровая схемотехника. Цифровые автоматы Мили и Мура Интересная часть речи В Русском языке живёт Кто что делает расскажет: Чертит, пишет иль поёт, Вышивает или пашет, Или забивает г
Интересная часть речи В Русском языке живёт Кто что делает расскажет: Чертит, пишет иль поёт, Вышивает или пашет, Или забивает г ADO technology
ADO technology Хэллоуин
Хэллоуин ДОЛГОСРОЧНАЯ ЦЕЛЕВАЯ ПРОГРАММА «ОДАРЕННЫЕ ДЕТИ КРАСНОЯРЬЯ» НА 2011–2013 ГОДЫ
ДОЛГОСРОЧНАЯ ЦЕЛЕВАЯ ПРОГРАММА «ОДАРЕННЫЕ ДЕТИ КРАСНОЯРЬЯ» НА 2011–2013 ГОДЫ Программа для шифрования и дешифрования текста особой важности
Программа для шифрования и дешифрования текста особой важности Обработка исключительных ситуаций. Исключения. Объекты класса Exception. (Тема 5.4)
Обработка исключительных ситуаций. Исключения. Объекты класса Exception. (Тема 5.4) Точка, прямая и плоскость на комплексном чертеже. (Лекция 2)
Точка, прямая и плоскость на комплексном чертеже. (Лекция 2) Мордовский народный костюм
Мордовский народный костюм ТЕПЛОВОЕ ИЗЛУЧЕНИЕ. Основные экспериментальные закономерности
ТЕПЛОВОЕ ИЗЛУЧЕНИЕ. Основные экспериментальные закономерности Презентация Понятие и содержание правоспособности граждан. Имя и место жительства гражданина
Презентация Понятие и содержание правоспособности граждан. Имя и место жительства гражданина Проект государственного/муниципального контракта: как правильно прописать основные условия его исполнения. (44-ФЗ)
Проект государственного/муниципального контракта: как правильно прописать основные условия его исполнения. (44-ФЗ) Регистрация НКО: пошаговая инструкция
Регистрация НКО: пошаговая инструкция Азбука архитектуры (8 класс)
Азбука архитектуры (8 класс)