Содержание
- 2. Подставив (2.2) в (2.1), получим При Т→∞ ω1=2π/T→0, а спектр – сплошным. Поэтому в выражении (2.3)
- 3. Подставив (2.2) в (2.1), получим (2.3) называется спектральной плотностью или спектральной характеристикой функции s(t). Внутренний интеграл,
- 4. В общем случае , когда пределы t1 и t2 не уточнены, спектральная плотность записывается в форме
- 5. Выражение (2.6) отличается от (1.13) только отсутствием множителя 2/Т. Следовательно, спектральная плотность обладает всеми основными свойствами
- 6. На основании формулы (2.8) нетрудно получить тригонометрическую форму интегрального преобразования (2.7): Отметим, что при ω=0 выражение
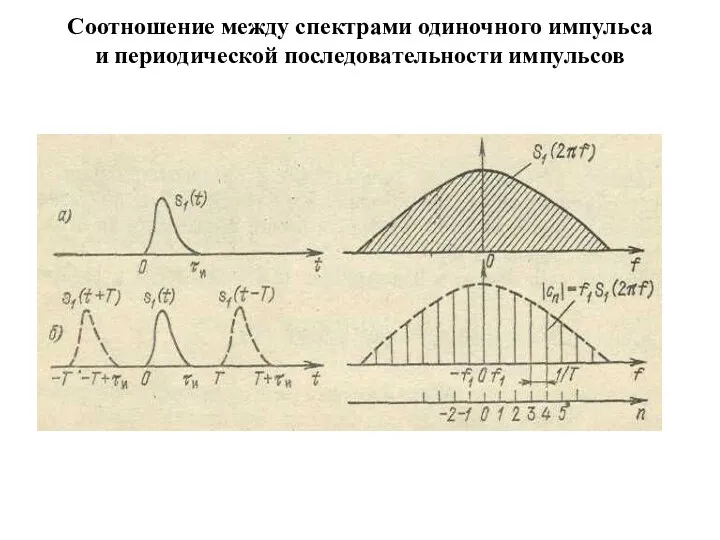
- 7. Соотношение между спектрами одиночного импульса и периодической последовательности импульсов
- 8. Коэффициент n-й гармоники в соответствии с выражением (1.13) Спектральная же плотность одиночного импульса на той же
- 10. Скачать презентацию






 Система таможенных органов в системе гос.управления в 15-16 веках Подготовили студенты группы ФТД-111, Васильев Станислав, Мухина Мар
Система таможенных органов в системе гос.управления в 15-16 веках Подготовили студенты группы ФТД-111, Васильев Станислав, Мухина Мар Средства измерения частоты вращения
Средства измерения частоты вращения  Приоритеты Российской Федерации в решении глобальных проблем
Приоритеты Российской Федерации в решении глобальных проблем Предмет эпидемиологии
Предмет эпидемиологии Мировые цивилизации
Мировые цивилизации Основы защиты от опасностей
Основы защиты от опасностей Василий Шукшин: режиссер, актер, писатель
Василий Шукшин: режиссер, актер, писатель Сантехнические изделия
Сантехнические изделия Презентация Разминка на тему: Субъекты трудового права
Презентация Разминка на тему: Субъекты трудового права  Календарные графики
Календарные графики  реферативная работа
реферативная работа Эскизирование деталей машин
Эскизирование деталей машин Архитектура и система команд процесоров Intel. (Тема 1)
Архитектура и система команд процесоров Intel. (Тема 1) Осенний осмотр 2019
Осенний осмотр 2019 Реформы Петра І и судьбы российской и украинской художественной культуры
Реформы Петра І и судьбы российской и украинской художественной культуры Производство бумаги
Производство бумаги Проектирование акселерометра с упругим подвесом
Проектирование акселерометра с упругим подвесом Қазақ тілі мен әдебиеті мамандығының
Қазақ тілі мен әдебиеті мамандығының Школа светофорных наук
Школа светофорных наук Smart metering
Smart metering Биотехнология стероидов и витаминов
Биотехнология стероидов и витаминов Многофункциональная металлическая опора Н=21-30 м лестницей с возможностью размещения до трех операторов связи
Многофункциональная металлическая опора Н=21-30 м лестницей с возможностью размещения до трех операторов связи Презентация на тему "За здоровий спосіб життя" - скачать презентации по Медицине
Презентация на тему "За здоровий спосіб життя" - скачать презентации по Медицине Порядок судебного разбирательства
Порядок судебного разбирательства Проект на тему: Легко ли быть предпринимателем Выполнила: студентка 021 группы специальности «Коммерция» Созонтова Виктория Влади
Проект на тему: Легко ли быть предпринимателем Выполнила: студентка 021 группы специальности «Коммерция» Созонтова Виктория Влади Теҙмә ҡушма һөйләмдәр
Теҙмә ҡушма һөйләмдәр О составе исполнительного комитета (центрального аппарата партии) в т.ч. задачи аналитической службы
О составе исполнительного комитета (центрального аппарата партии) в т.ч. задачи аналитической службы Долг и совесть - презентация для начальной школы
Долг и совесть - презентация для начальной школы