Содержание
- 2. Изменение масштаба времени s2(t)=s1(nt), n > 1. Вводя новую переменную интегрирования τ=nt, получаем При сжатии сигнала
- 3. Смещение спектра сигнала Применим (2.6) к произведению s(t)cos(ω0t+θ0) Из выражения (2.16) вытекает, что расщепление спектра на
- 4. Дифференцирование и интегрирование сигнала *Производная функции еiωt равна iωеiωt. (2.17) Аналогичным образом можно показать, что сигналу
- 5. Сложение сигналов Так как преобразование Фурье является линейным, очевидно, что при сложении сигналов s1(t), s2(t),..., обладающих
- 6. (2.20) В частном случае ω=0 Заменяя х на ω, получаем (2.21) Здесь
- 7. Аналогично можно показать, что произведению двух спектров соответствует функция времени s(t), являющаяся сверткой функций f(t) и
- 8. Взаимная заменяемость ω и t в преобразованиях Фурье Если s(t) есть функция, четная относительно t, то
- 9. Из п. 1 вытекает, что при четной функции s(t) можно произвольно выбирать знак перед t в
- 11. Скачать презентацию




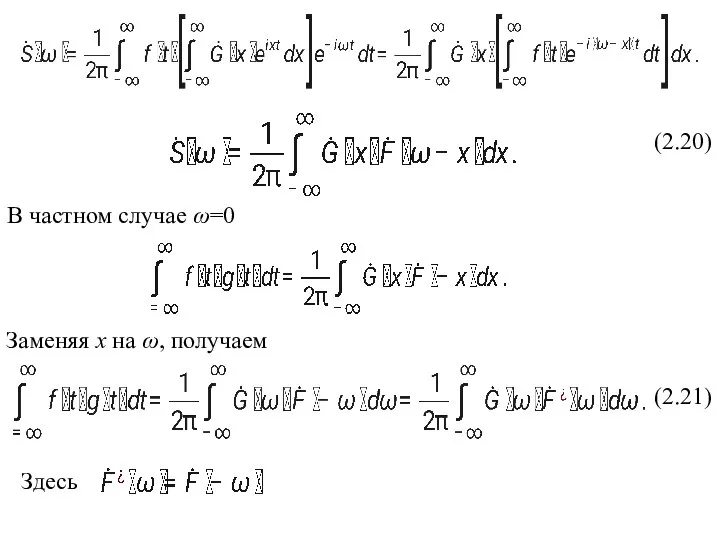



 Партія регіонів
Партія регіонів Спуск с горы на лыжах – техника выполнения
Спуск с горы на лыжах – техника выполнения Motronic
Motronic Mikołaj Święty
Mikołaj Święty Заимствованные слова
Заимствованные слова СТРИОПАЛЛИДАРНАЯ СИСТЕМА. МЕТОДИКА ИССЛЕДОВАНИЯ. СИНДРОМЫ ПОРАЖЕНИЯ
СТРИОПАЛЛИДАРНАЯ СИСТЕМА. МЕТОДИКА ИССЛЕДОВАНИЯ. СИНДРОМЫ ПОРАЖЕНИЯ Теоретико-методологические основы изучения истории общественных движений и политических партий
Теоретико-методологические основы изучения истории общественных движений и политических партий Двумерные массивы в формате powerpoint
Двумерные массивы в формате powerpoint Применение международных стандартов для повышения качества экспертного производства
Применение международных стандартов для повышения качества экспертного производства Особенности расчета прямозубых конических передач
Особенности расчета прямозубых конических передач Железобетонные и каменные конструкции. Сущность железобетона
Железобетонные и каменные конструкции. Сущность железобетона Традиции и обычаи Германии
Традиции и обычаи Германии Принципы и схемы лечения при заболевании костей и суставов
Принципы и схемы лечения при заболевании костей и суставов  Проект скловарної печі для виробництва сортового скла продуктивністю 125 т\ добу
Проект скловарної печі для виробництва сортового скла продуктивністю 125 т\ добу The Civil War and after war years
The Civil War and after war years Розвиток української мови на сучасному етапі
Розвиток української мови на сучасному етапі Решение творческих задач с элементами конструирования
Решение творческих задач с элементами конструирования ХЛЕБ – ВСЕМУ ГОЛОВА Работа учащейся 3 класса МОУ СОШ №20 с. Лувеньга Вальсовой Дарьи
ХЛЕБ – ВСЕМУ ГОЛОВА Работа учащейся 3 класса МОУ СОШ №20 с. Лувеньга Вальсовой Дарьи Жанна д’Арк Национальная героиня Франции
Жанна д’Арк Национальная героиня Франции Параллельное выполнение транзакций. Типы конфликтов. Захваты и блокировки
Параллельное выполнение транзакций. Типы конфликтов. Захваты и блокировки Синтаксис программы, операторы, комментарии, техника программирования. Основные принципы программирования
Синтаксис программы, операторы, комментарии, техника программирования. Основные принципы программирования Введение в культурологию
Введение в культурологию Симметричные многопроцессорные системы
Симметричные многопроцессорные системы Политическое лидерство
Политическое лидерство Презентация Временное хранение товаров
Презентация Временное хранение товаров Межнациональные особенности невербального общения Выполнила студентка группы Ю-104 Чуева Яна
Межнациональные особенности невербального общения Выполнила студентка группы Ю-104 Чуева Яна  Системы массового обслуживания (СМО)
Системы массового обслуживания (СМО) Вовлечение молодежи
Вовлечение молодежи