Содержание
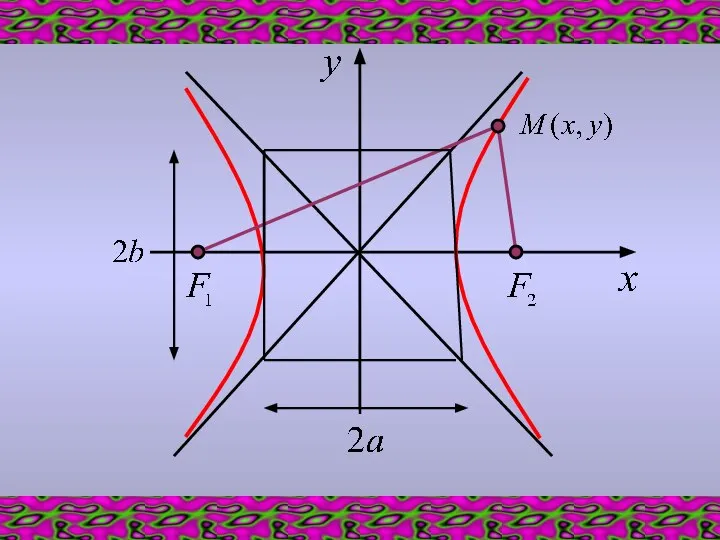
- 3. Введем обозначения: a – действительная полуось гиперболы b – мнимая полуось гиперболы Для любой точки М(х,у),
- 4. Прямые, проходящие через начало координат и имеющие угловые коэффициенты и называются асимптотами гиперболы. Асимптоты делят плоскость
- 5. ТЕОРЕМА Для того, чтобы точка М(х,у) принадлежала гиперболе, необходимо и достаточно, чтобы ее координаты удовлетворяли уравнению
- 6. Покажем, что координаты точки, принадлежащей гиперболе, удовлетворяют уравнению (2). Т.к. точка М(х,у) принадлежит гиперболе, то по
- 7. Тогда:
- 8. Возводим в квадрат обе части выражения:
- 9. Возводим в еще раз квадрат: Делим все выражение на
- 10. каноническое уравнение гиперболы
- 11. Отношение фокусного расстояния к длине действительной оси гиперболы называется ЭКСЦЕНТРИСИТЕТОМ
- 13. Скачать презентацию





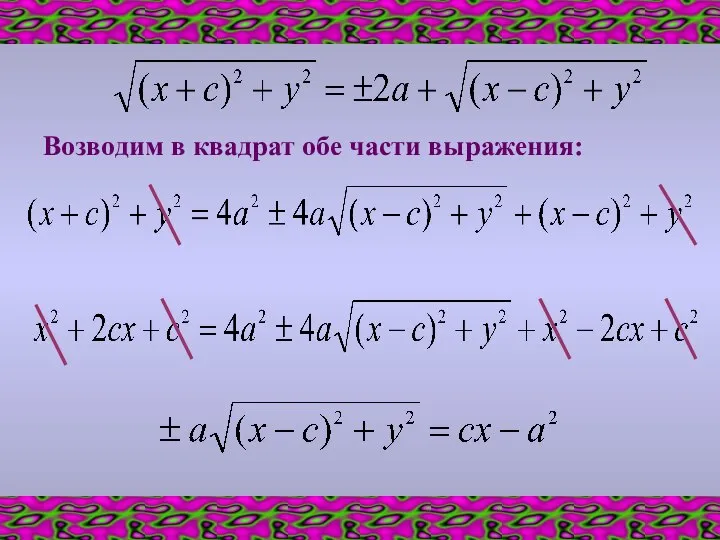
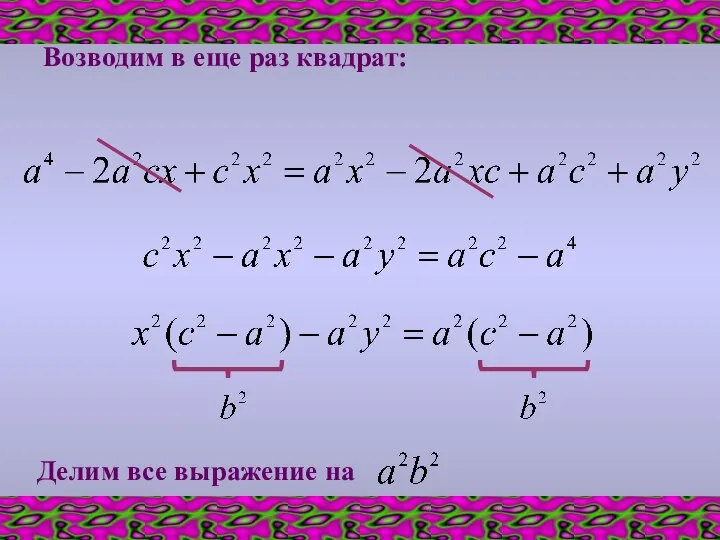


 Система визуального объектно-ориентированного программирования Delphi
Система визуального объектно-ориентированного программирования Delphi Политическая сфера
Политическая сфера Управленческие решения в системе менеджмента
Управленческие решения в системе менеджмента Company confidential Lenovo S660 Service Manual
Company confidential Lenovo S660 Service Manual Супрематизм. Казимир Северинович Малевич
Супрематизм. Казимир Северинович Малевич Коми-зыряне
Коми-зыряне Пленэрная живопись
Пленэрная живопись Презентация «ЗАЕМ И КРЕДИТ»
Презентация «ЗАЕМ И КРЕДИТ» PowerShell: Познать за 9 часов
PowerShell: Познать за 9 часов Летние виды спорта
Летние виды спорта Воры в законе
Воры в законе Презентация Активные методы обучения
Презентация Активные методы обучения Тренинг-семинар Профилактика синдрома эмоционального выгорания педагогов.
Тренинг-семинар Профилактика синдрома эмоционального выгорания педагогов. Язык библиографического описания
Язык библиографического описания Дресс-код для школы
Дресс-код для школы Национализм как политичская практика
Национализм как политичская практика Российский государственный педагогический университет им. А.И.Герцена Факультет безопасности жизнедеятельности «Синдром Да
Российский государственный педагогический университет им. А.И.Герцена Факультет безопасности жизнедеятельности «Синдром Да Презентация____
Презентация____ ФИНАНСОВЫЙ МЕНЕДЖМЕНТ
ФИНАНСОВЫЙ МЕНЕДЖМЕНТ  Препроцессор языка «С». Директивы препроцессора. Модули и модульное программирование
Препроцессор языка «С». Директивы препроцессора. Модули и модульное программирование Невмержицкая Елена Викторовна ЭТНООРИЕНТИРОВАННАЯ МЕТОДИКА ОБУЧЕНИЯ ИНОСТРАННОМУ ЯЗЫКУ В СИСТЕМЕ СРЕДНЕГО ПРОФЕССИОНАЛЬ
Невмержицкая Елена Викторовна ЭТНООРИЕНТИРОВАННАЯ МЕТОДИКА ОБУЧЕНИЯ ИНОСТРАННОМУ ЯЗЫКУ В СИСТЕМЕ СРЕДНЕГО ПРОФЕССИОНАЛЬ 58.Законодательство по охране труда Подготовила Студентка группы Э121Б Кондратенко Эльвира
58.Законодательство по охране труда Подготовила Студентка группы Э121Б Кондратенко Эльвира Микропроцессорные системы (МПС): работа первичного управляющего автомата в режиме прерывания и в режиме захвата шины
Микропроцессорные системы (МПС): работа первичного управляющего автомата в режиме прерывания и в режиме захвата шины Теория и методика физической культуры, как наука и учебный предмет
Теория и методика физической культуры, как наука и учебный предмет Особливості сучасних монархій: західні і східні моделі
Особливості сучасних монархій: західні і східні моделі Использование логико-структурного подхода в современной практике проектного планирования. Тема 4
Использование логико-структурного подхода в современной практике проектного планирования. Тема 4 Семантика языка Prolog
Семантика языка Prolog Нині радість стала
Нині радість стала