Графическая иллюстрация свойств дискретного преобразования Фурье

Получим дискретное преобразование Фурье (ДПФ) для этого вектора, что символически

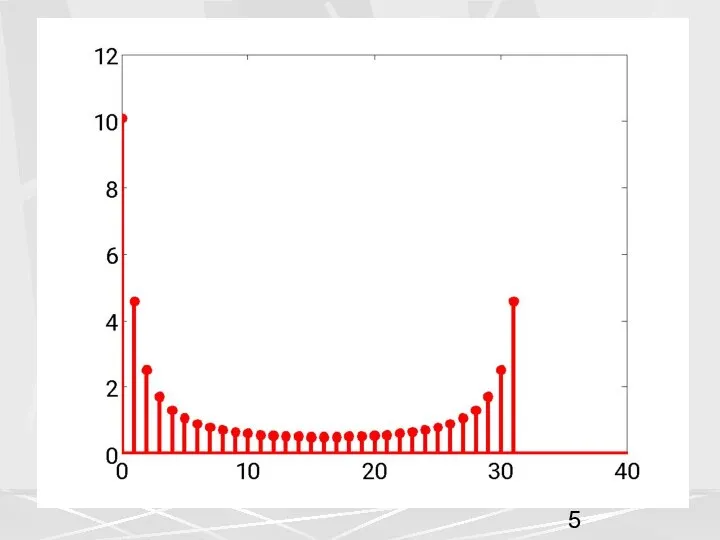
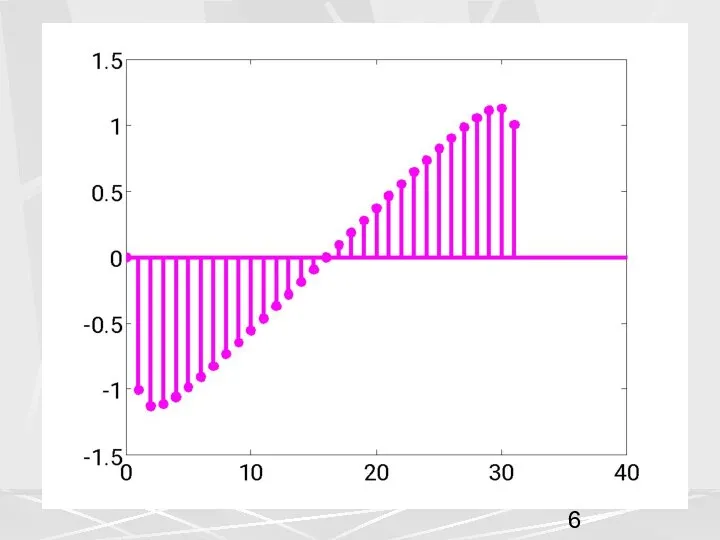
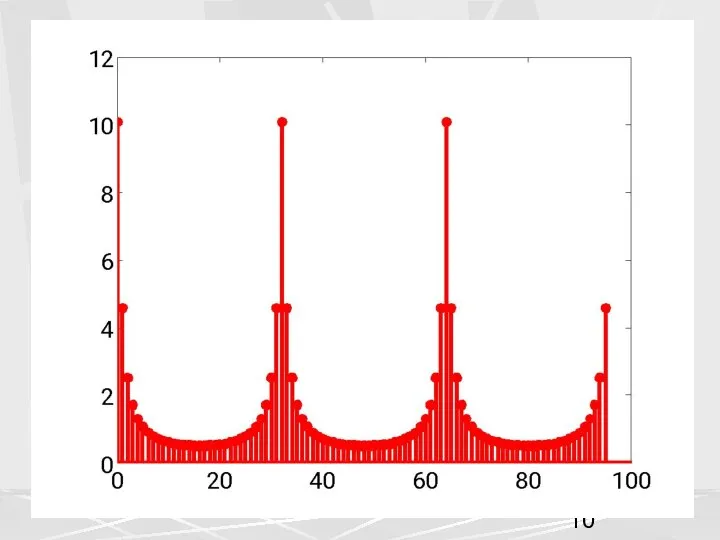
Последовательность , является, вообще говоря, последовательностью комплексных чисел. Поэтому интересно

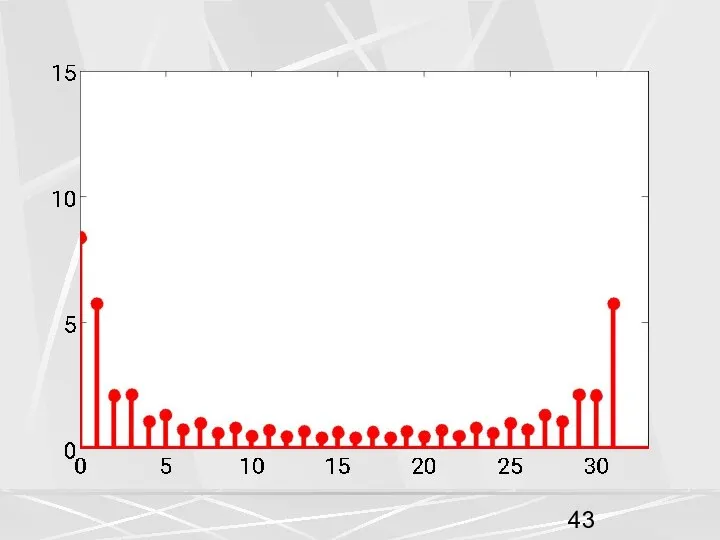
Если ДПФ (2) рассматривать для любых значений индекса k, то

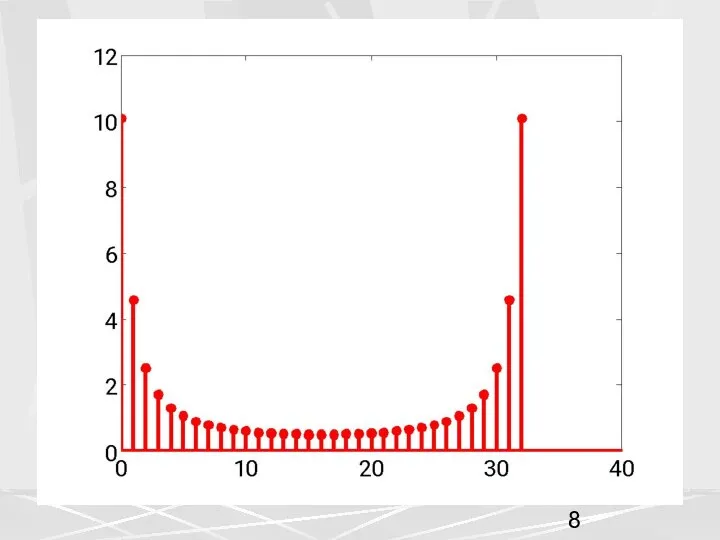
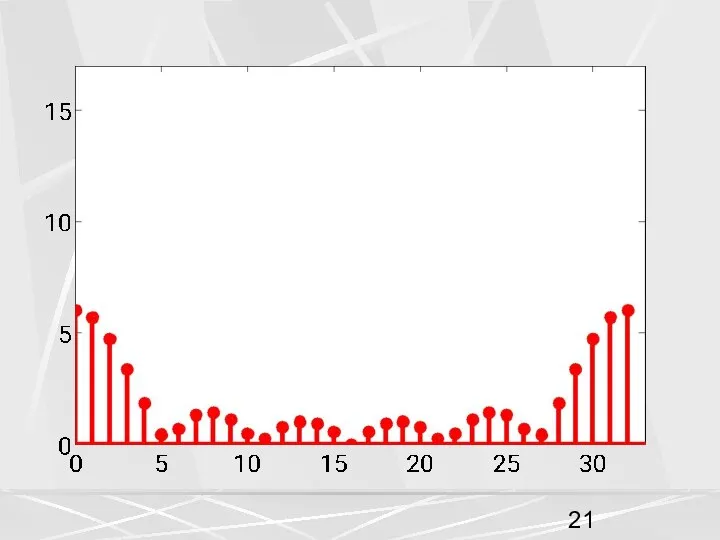
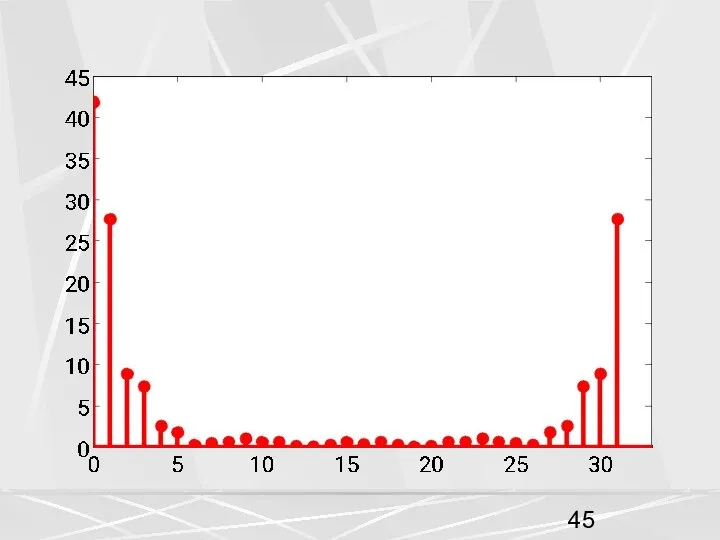
На этом рисунке можно увидеть еще одно свойство. График АЧХ

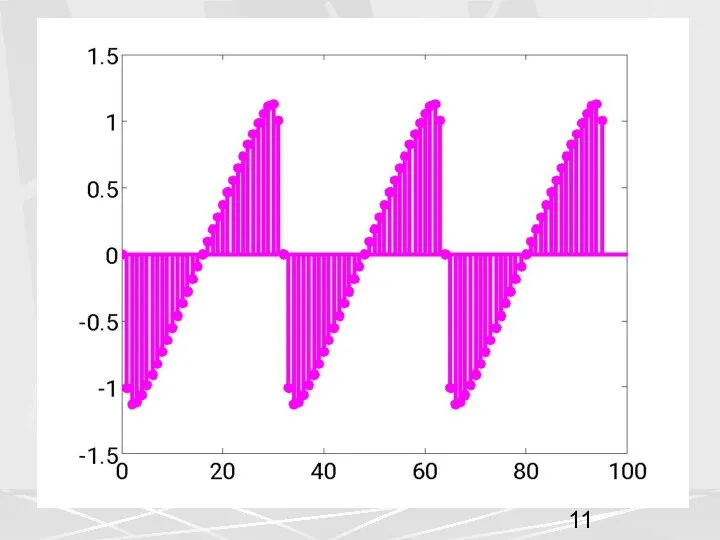
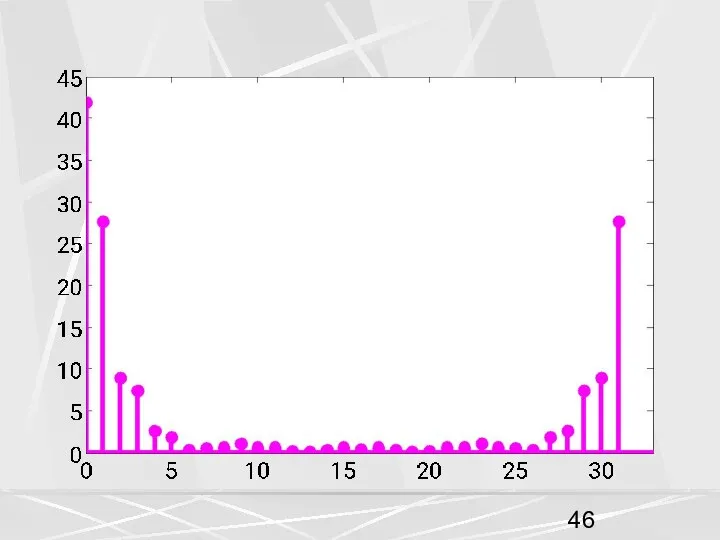
Теперь обратимся к свойствам ДПФ, рассмотренным на предыдущей лекции.

1.

Для нашего примера N = 32 , это для модуля

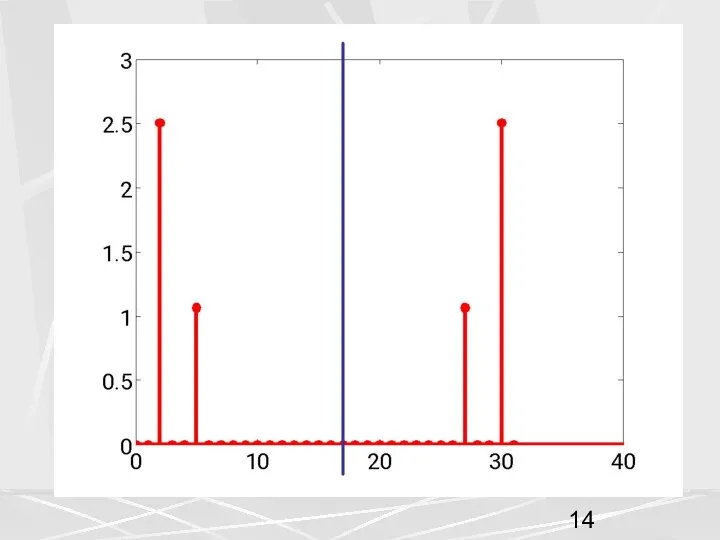
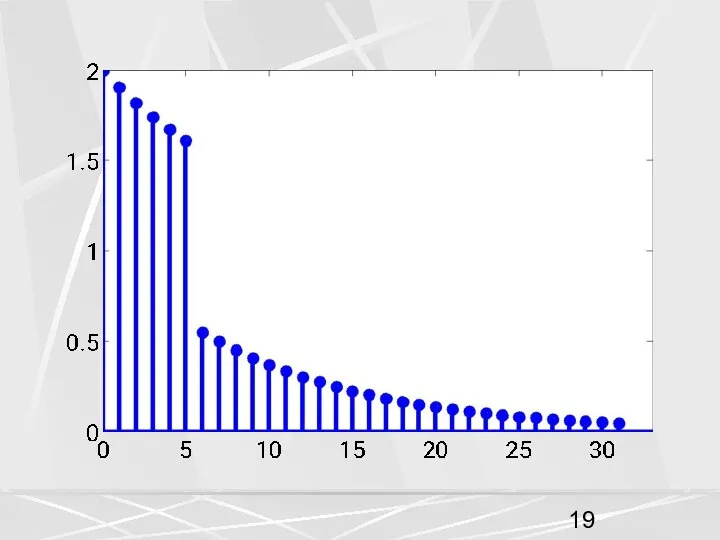
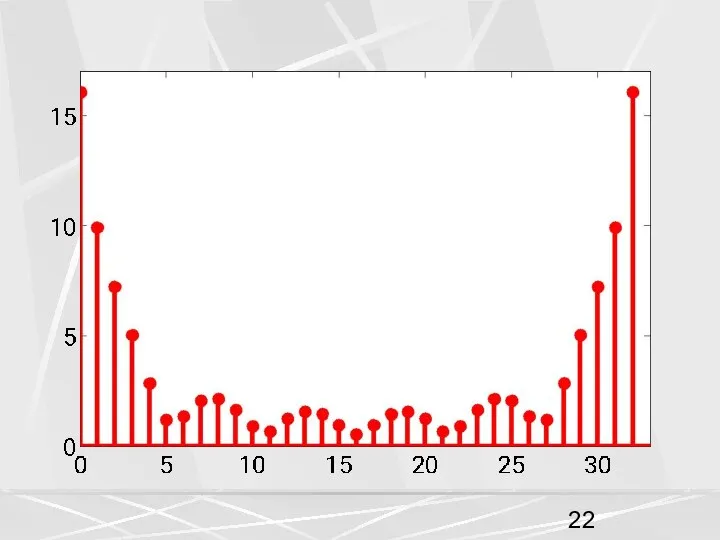
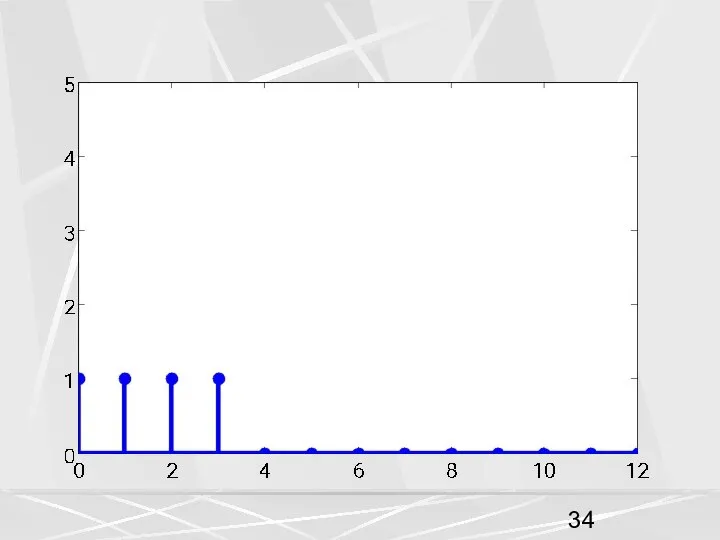
2. Линейность. Линейной комбинации векторов соответствует линейная комбинация ДПФ.

(9)

В

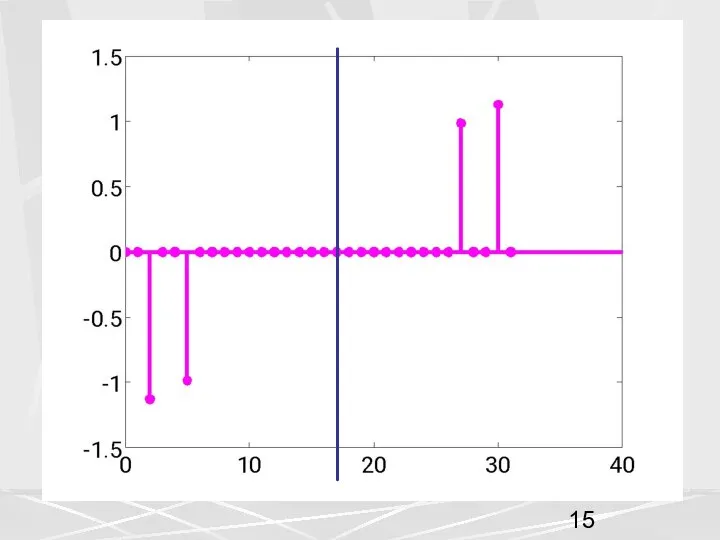
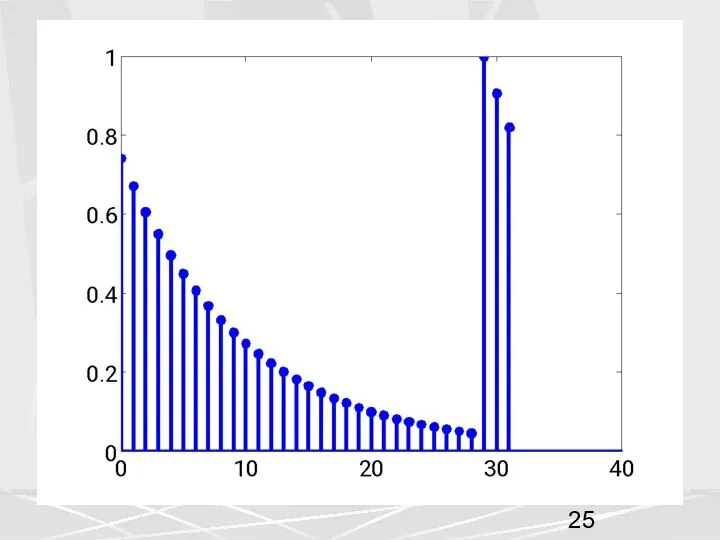
3. Циклический сдвиг влево на m позиций. Циклическому сдвигу влево на

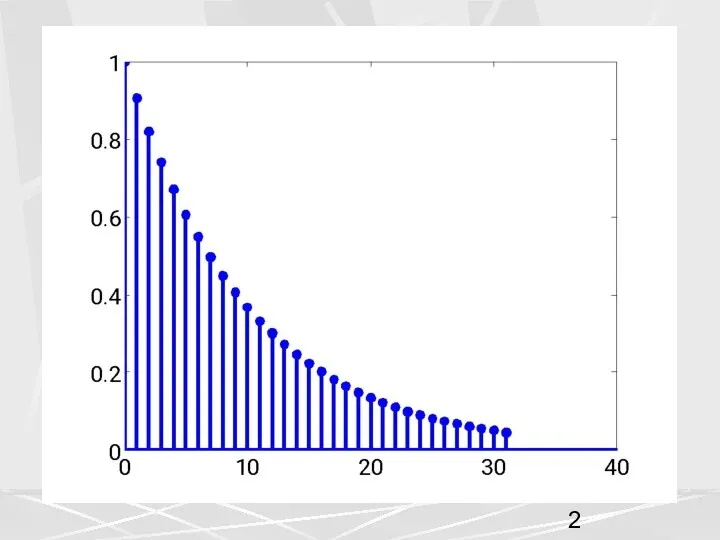
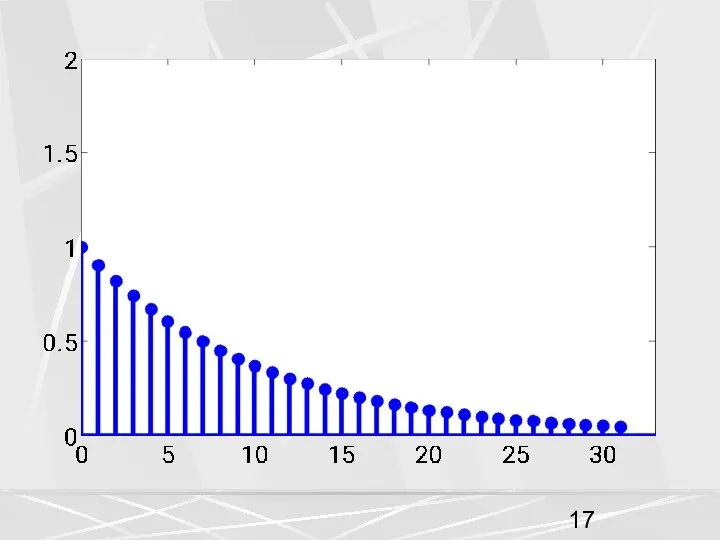
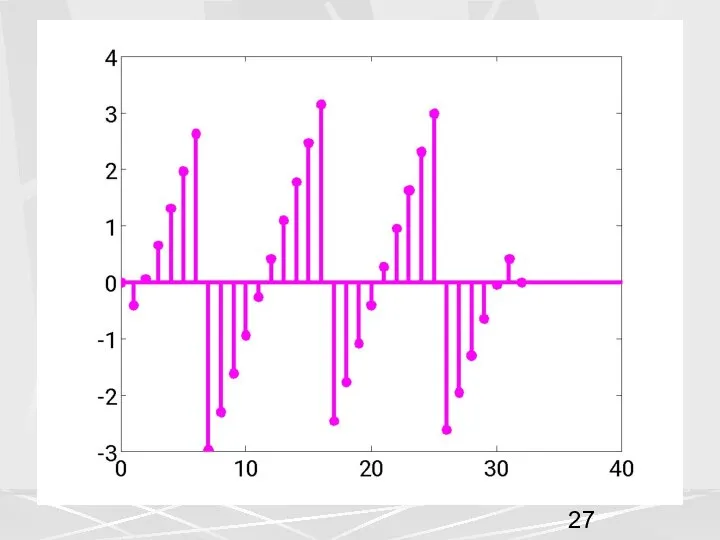
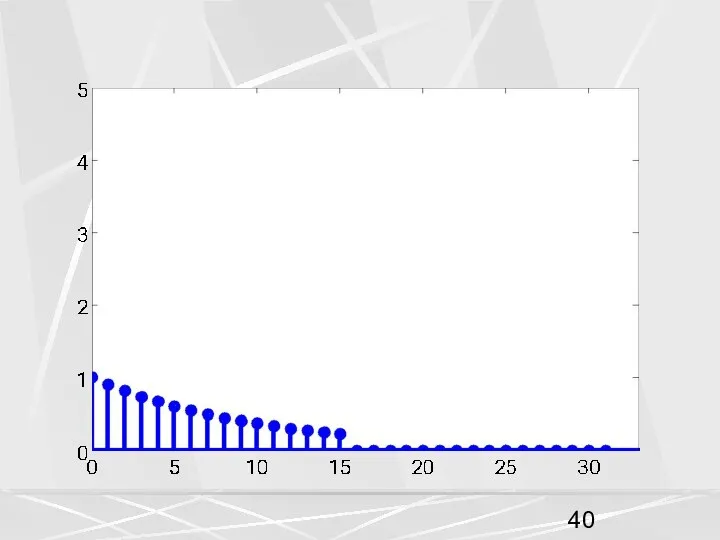
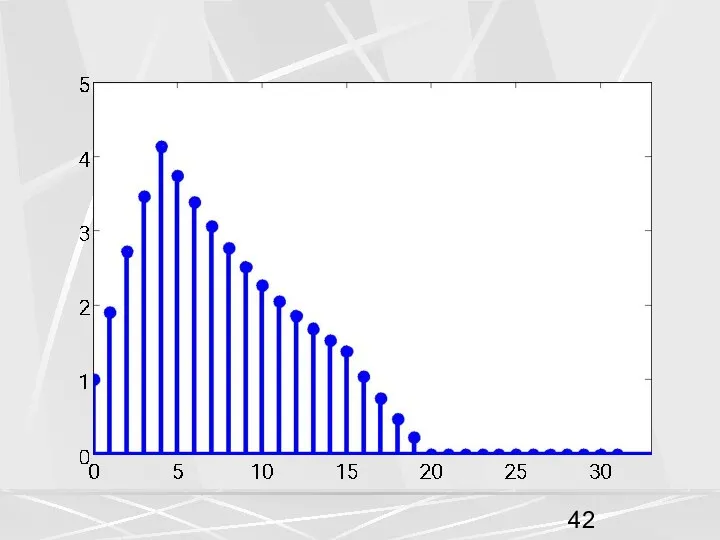
Рассмотрим для примера, последовательность, рассмотренную выше (1) у которой компоненты

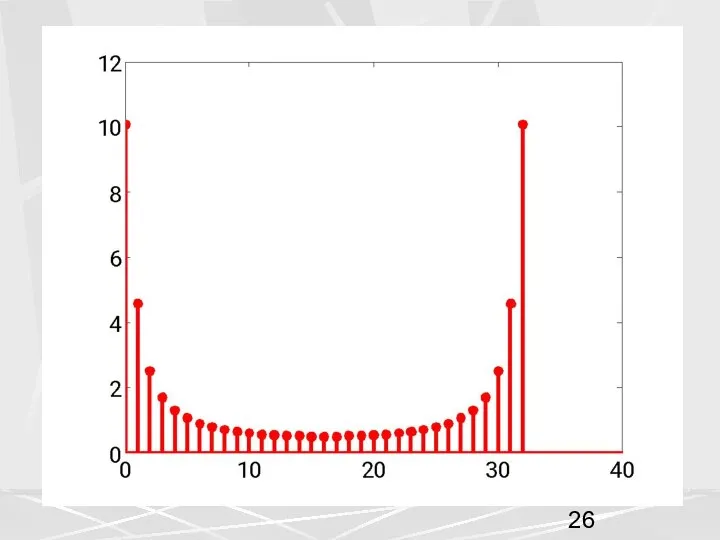
Определение. Под сверткой двух векторов и с периодом N ,

Обратим внимание на следующие свойства свертки.
Первое, если периоды векторов a

Третье, если периоды векторов a и b разные и равны и

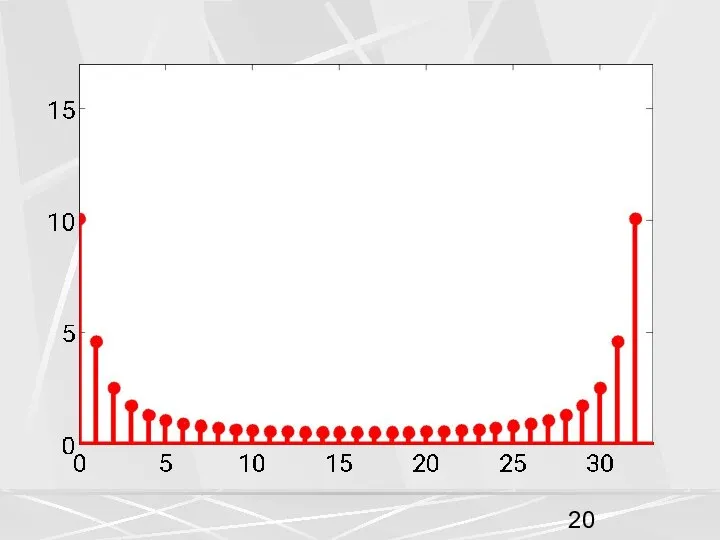
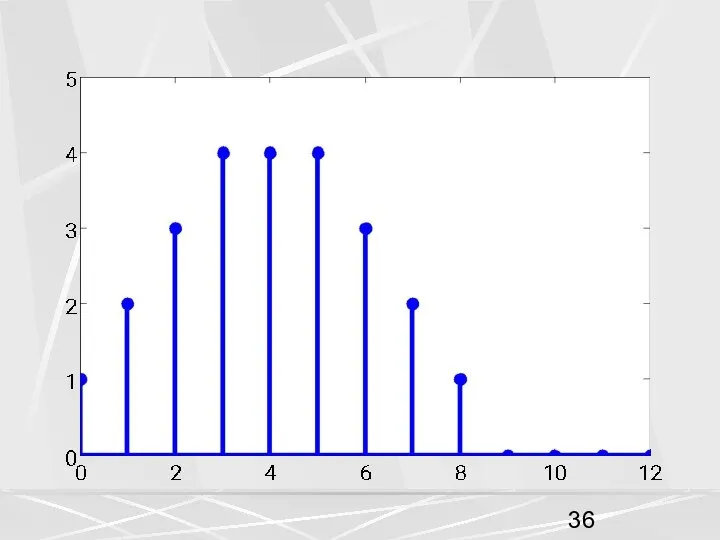
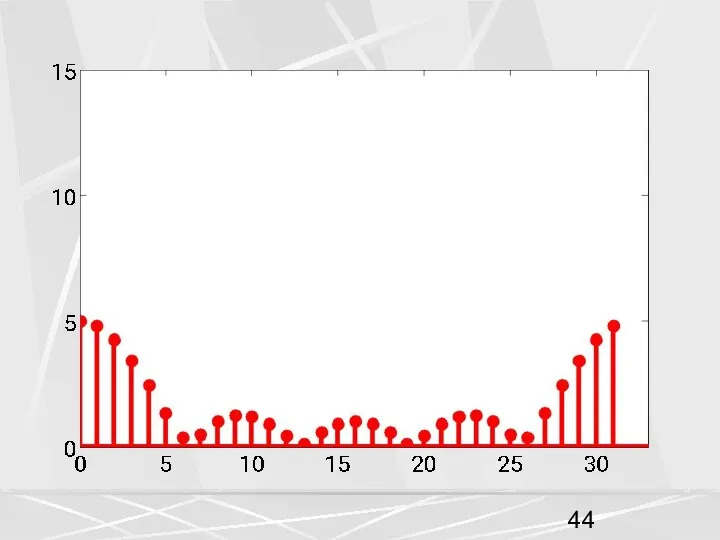
Свойство ДПФ свертки векторов. Вектор являющийся сверткой двух других векторов имеет

Поэтому ДПФ (2) для всех трех векторов a, b, c

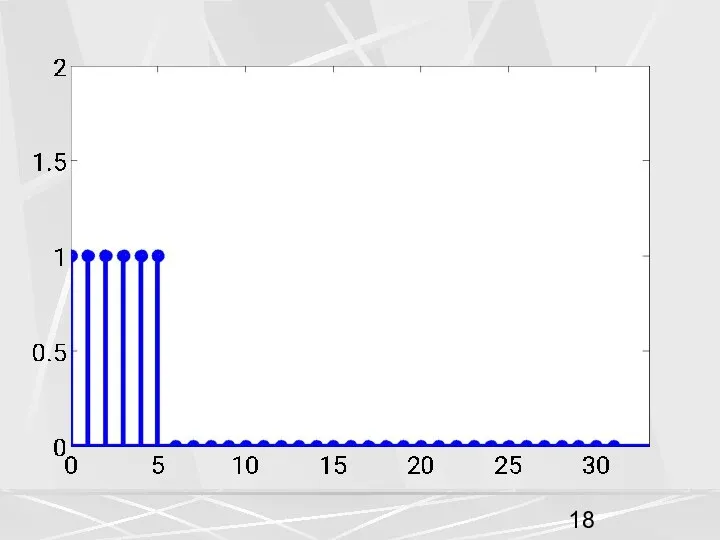
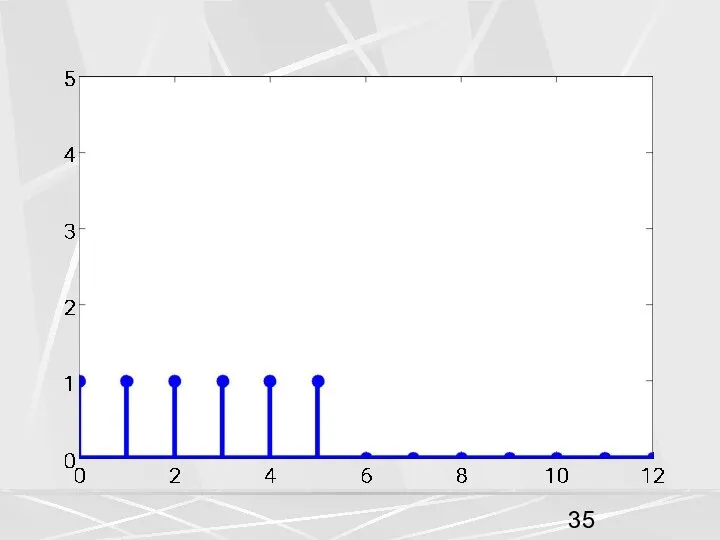
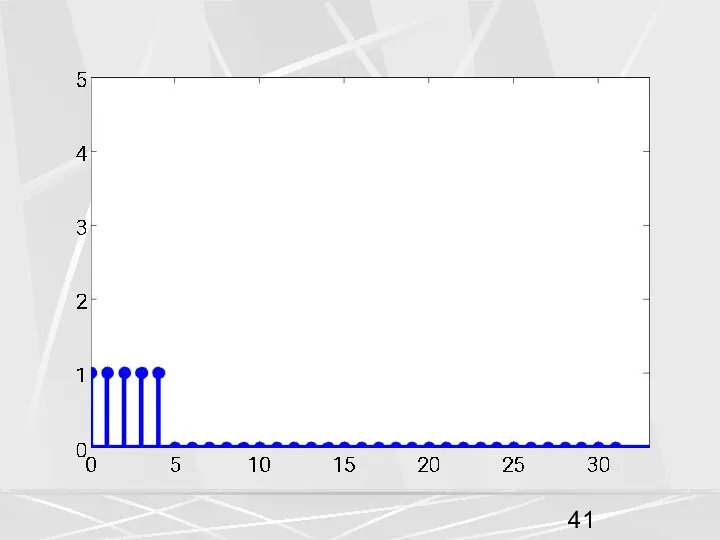
Пусть компоненты второго вектора имеют вид единичной ступеньки.

(32)

Эти

Дискретное преобразование Фурье и пакет MATLAB

В пакете MATLAB имеются средства

Обратное дискретное преобразование Фурье ОДПФ, выполняет функция ifft(X) . Вызов

Эти формулы в пакете MATLAB выглядят следующим образом.

(34)

Отличие

Дискретное преобразование Фурье и спектр сигналов

До сих пор дискретное преобразование

Здесь F - частота Найквиста, а отсчеты дискретного сигнала. Предположим,

Спектр дискретного сигнала (36) является непрерывной периодической функцией с периодом

Мы видим, что сумма, стоящая в формуле (38) является ДПФ

Таким образом, дискретный спектр дискретного сигнала выражается через ДПФ от

Поэтому можно сказать, что дискретное преобразование Фурье является по сути

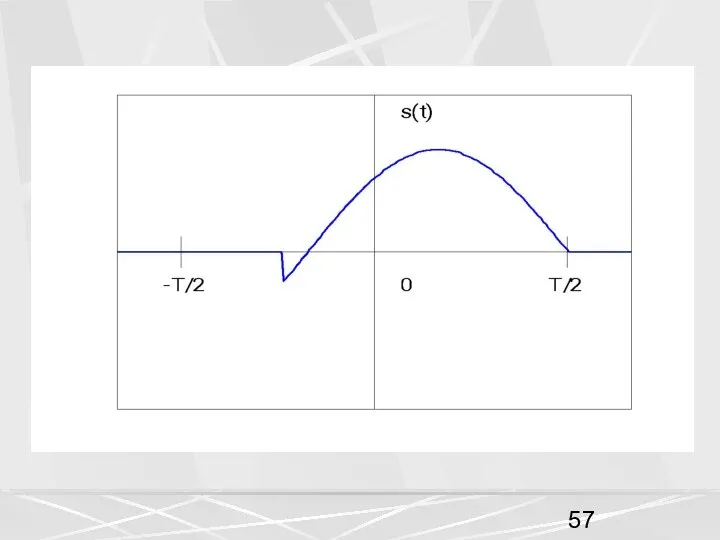
Если преобразование Фурье сводится к аналитическим выражениям, то задача нахождения

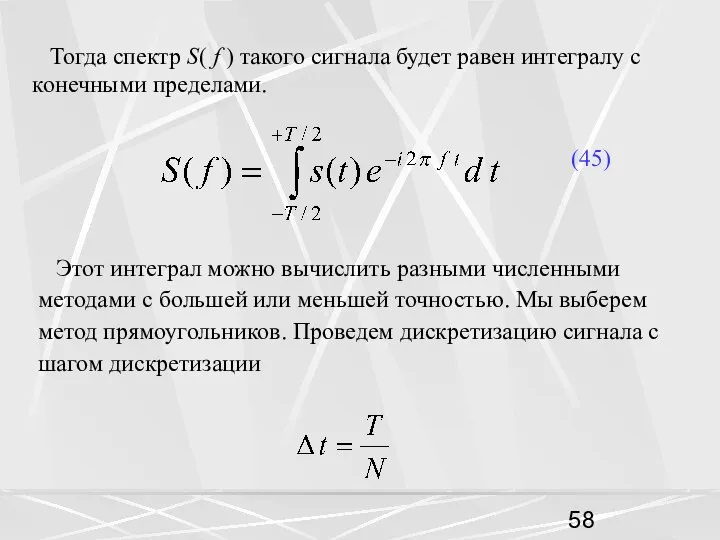
Тогда спектр S( f ) такого сигнала будет равен интегралу

где N для удобства четное число. Отсчеты сигнала берем в

Выразим шаг дискретизации через частоту Найквиста

Тогда формула (46) примет вид

(47)

Сравним формулу (47) с выражением (36) для спектра дискретного сигнала.

Это связано с тем, что в интеграле (45) мы рассматриваем

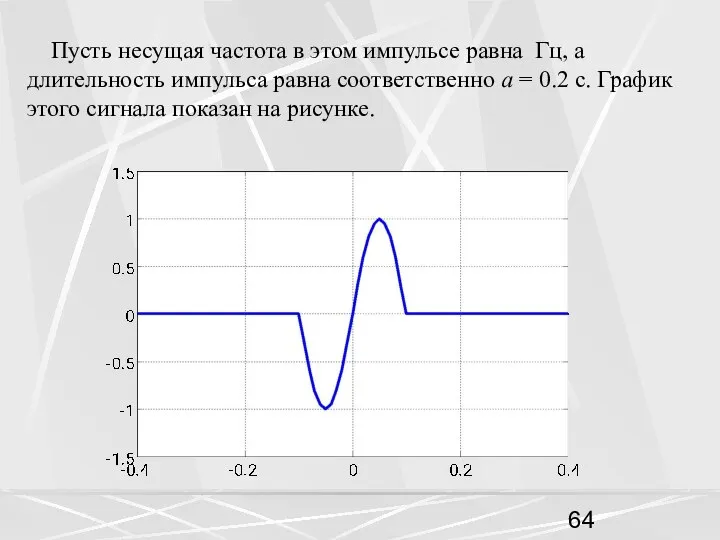
Подставляем дискретные частоты (50) в формулу (47) и получаем

(51)

Пусть несущая частота в этом импульсе равна Гц, а длительность

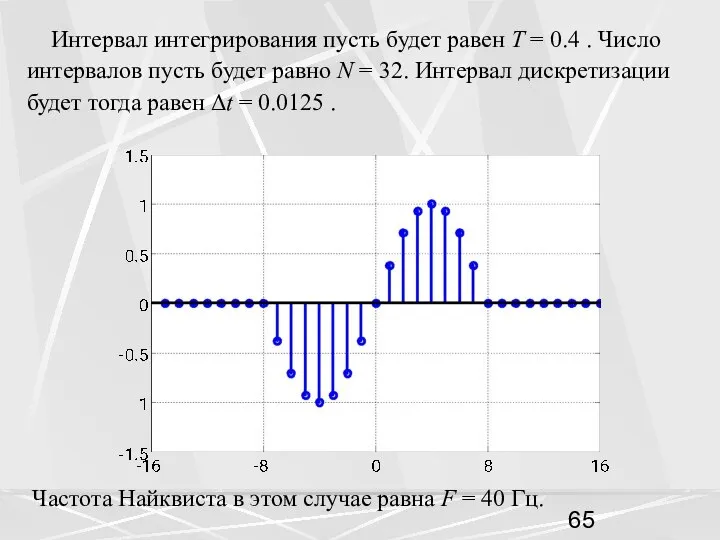
Интервал интегрирования пусть будет равен T = 0.4 . Число

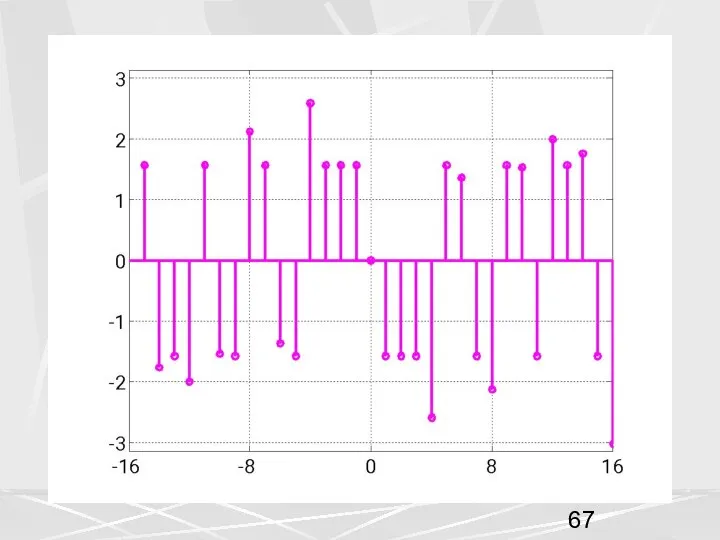
Изменим нумерацию компонент дискретного сигнала , чтобы это было похоже

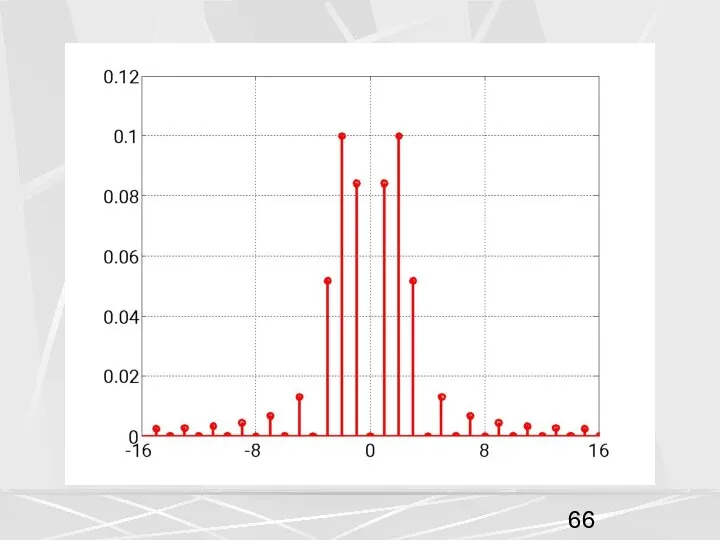
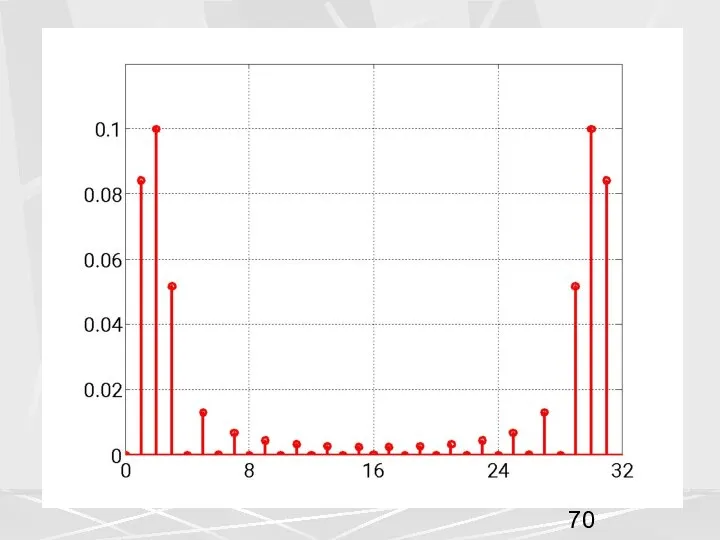
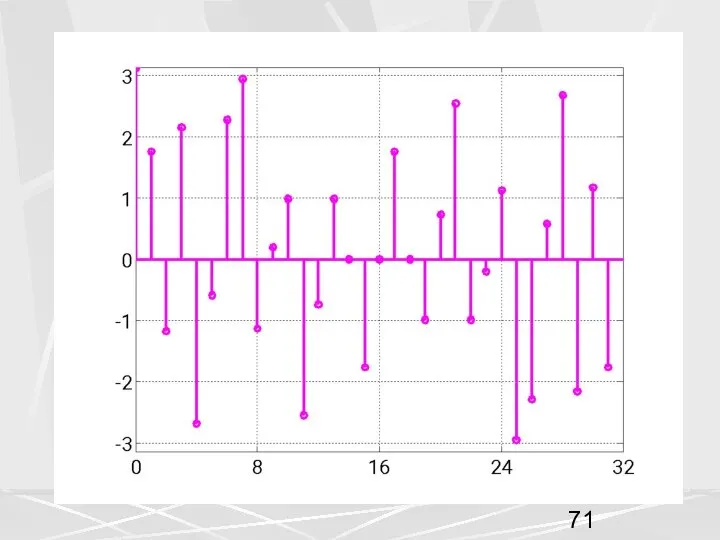
Вместо спектра заданного формулой (51) рассмотрим спектр, полученный с помощью

Простой анализ показывает, что связь между компонентами дискретного спектра (51)

Быстрое преобразование Фурье (БПФ)

Для быстрой спектральной обработки сигналов, надо иметь

В этом алгоритме важным моментом является число членов N суммы

Для вычисления каждого коэффициента y(k) , как легко видеть, требуется

Введем вектор:

(61)

который является вектором нечетных отсчетов вектора X. Учтем следующее

Далее разобьем сумму (59) на два слагаемых с четными и

Сравнивая соотношения (64) с формулой (59), мы видим, что первая

(66)

! Доказать самостоятельно соотношения (66).

Сделаем в (65) замену и

Объединим формулы (65), (67)

(68)

Подведем некоторый итог. При помощи уравнений

через коэффициенты ДПФ размерности .

(70)

Таким образом, вычисление - точечного

Итого, реализация ДПФ размерности с использованием уравнений (68) потребует порядка