Содержание
- 2. Теорема 2. (Теорема отсчетов). Если сигнал s(t) имеет спектр ограниченный полосы, т.е. S(f) = 0 при
- 3. Доказательство. Выразим сигнал через его спектр (60) Тогда с использованием формул (56, 57) получаем выражение для
- 4. Спектр S(f) , принимающий ненулевые значения только на отрезке f ∈ [-F, F] , периодически продолжим
- 5. Тогда получаем (63) Здесь при переходе от первой суммы ко второй была совершена замена
- 6. Берем формулу для сигнала (59) и заменяем в ней спектр S(f) на спектр (63) (64) Меняя
- 7. Отсюда, учитывая, что интеграл в (65) равен (66) получаем утверждение теоремы. ! Доказать справедливость формулы (66).
- 8. Итак, шаг дискретизации Δt позволяет точно восстановить аналоговый сигнал, если его спектр ограничен условием (67) Отсюда,
- 9. Это условие можно записать через частоту Найквиста F (69) Другими словами, при дискретизации аналогового сигнала частоту
- 10. Дискретное преобразование Фурье Введем два числовых вектора x и X размерности N. (1) Компоненты этих векторов
- 11. Соотношение (2) носит название дискретного преобразования Фурье (ДПФ). Иногда говорят, что вектор является дискретным преобразованием вектора
- 12. Теорема 1. Вектор можно восстановить при помощи обратного дискретного преобразования Фурье (ОДПФ), которое определяется формулой. (3)
- 13. В выражении (4) поменяем порядок суммирования. (5) Вычислим сумму, стоящую в скобках в формуле (5) (6)
- 14. Используем формулу суммы геометрической прогрессии (7) для вычисления суммы (6). (8) В последнем выражении применяем формулу
- 15. В результате формула (8) принимает вид. (9) В выражении (9) n и m целые числа принимают
- 16. Таким образом, если n ≠ m , сумма в выражении (6) равна нулю. (10) Если же
- 17. Подставляем (12) в формулу (5), и используем свойство символа Кронекера, сворачивать сумму. В результате получаем (13)
- 18. Можно сказать, что вектор и вектор , связаны между собой дискретным преобразованием Фурье, что обычно изображают
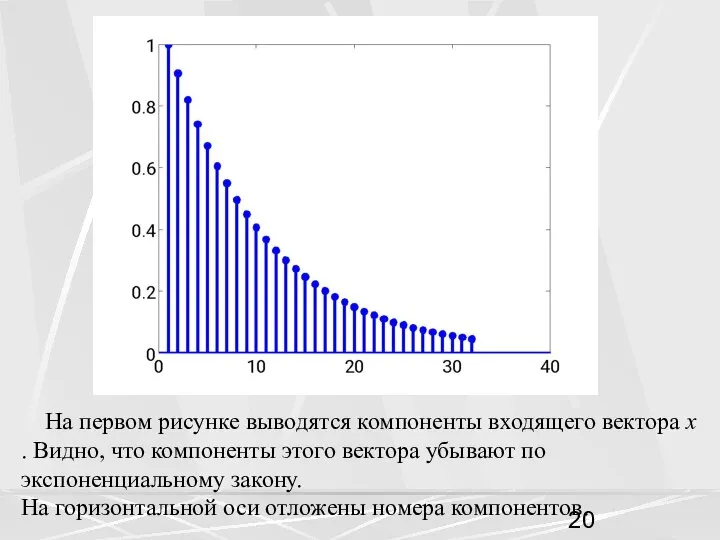
- 19. Фрагмент кода программы показывает, как можно получить ДПФ для заданного вектора x , компоненты которого убывают
- 20. На первом рисунке выводятся компоненты входящего вектора x . Видно, что компоненты этого вектора убывают по
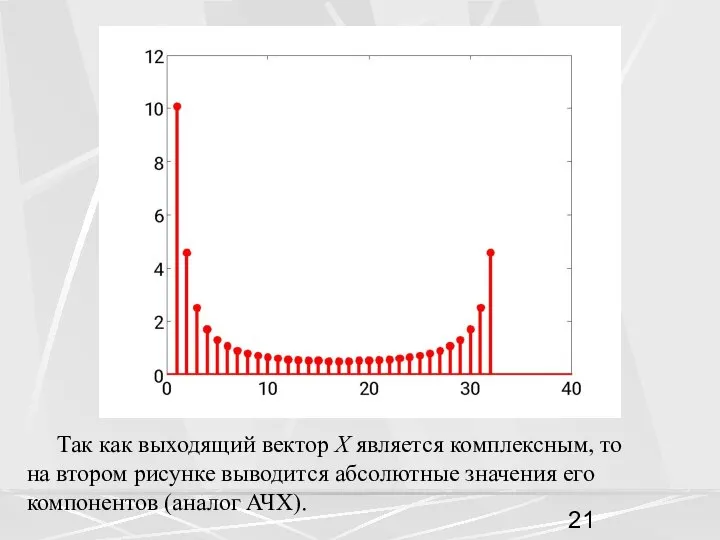
- 21. Так как выходящий вектор X является комплексным, то на втором рисунке выводится абсолютные значения его компонентов
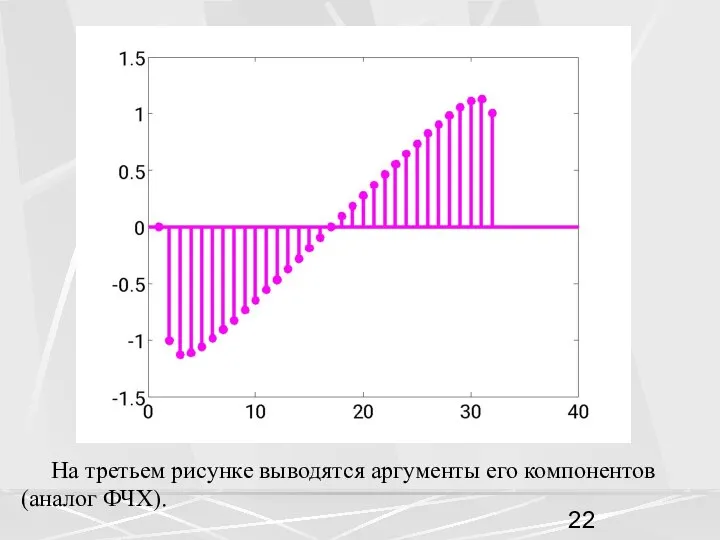
- 22. На третьем рисунке выводятся аргументы его компонентов (аналог ФЧХ).
- 23. Обратное дискретное преобразование Фурье ОДПФ, выполняет функция ifft(X) . Вызов этой функции осуществляется следующим образом. x
- 24. Свойства дискретное преобразование Фурье Отметим важные свойства ДПФ, которые часто используются в приложениях. Сначала несколько слов
- 25. 1. Свойства симметрии. Если вещественный вектор x с периодом N имеет в качестве ДПФ вектор X
- 26. Из соотношений (16) вытекают условия симметрии для действительных и мнимых частей компонент вектора X . (17)
- 27. 2. Линейность. Линейной комбинации векторов соответствует линейная комбинация ДПФ. (18) ! Доказать самим соотношения (18).
- 28. 3. Циклический сдвиг влево. Циклическому сдвигу влево компонент вектора-сигнала, соответствует умножение компонент вектора-сигнала на фазовый множитель.
- 29. Заменим в формуле (20) компоненты вектора y на компоненты вектора x с помощью условия (19.) (21)
- 30. Далее выполняем в выражении (21) следующие преобразования. (22) Последняя сумма в выражении (22) является ДПФ для
- 31. Следствие. Циклический сдвиг влево на m позиций. Циклическому сдвигу влево на m позиций компонент вектора-сигнала, соответствует
- 32. 4. Циклический сдвиг вправо на m позиций. Циклическому сдвигу вправо на m позиций компонент вектора-сигнала, соответствует
- 33. Следствие из свойств 3, 4. Инвариантность амплитудного спектра относительно циклических сдвигов. При любом циклическом сдвиге амплитуда
- 34. Теперь вычислим модуль от выражения (25). (26) В формуле (26) учтено, модуль фазового множителя равен единице.
- 35. Определение. Под сверткой двух векторов и с периодом N , будем понимать вектор с периодом 2N
- 36. Доказательство. Дополним векторы a и b нулями, чтобы они имели период 2N . Выпишем ДПФ для
- 37. Для удобства введем обозначение (30) Выпишем ДПФ вектора-свертки с использованием формул (28), (29), (30). (31)
- 38. В формуле (31) изменен порядок суммирования. В сумме в скобках (31) сделаем замену индексов В результате
- 39. Теперь учтем, что компоненты векторов a и b отличны от нуля только для следующих значений индексов
- 40. Далее, так как для l > N – 1, то суммы в (33) не изменяться, если
- 41. С учетом формул (34) выражение (33) принимает искомый вид. Свойство доказано. Дискретное преобразование Фурье и спектр
- 42. Здесь F - частота Найквиста, а отсчеты дискретного сигнала. Предположим, что дискретный сигнал определен конечным набором
- 43. Спектр дискретного сигнала (36) является непрерывной периодической функцией с периодом 2F . На периоде [0, 2F]
- 44. Мы видим, что сумма, стоящая в формуле (38) является ДПФ для последовательности . (39) Сравнивая формулы
- 45. Таким образом, дискретный спектр дискретного сигнала выражается через ДПФ от дискретного сигнала по формуле (40). Если
- 46. Теперь рассмотрим, как связано дискретное преобразование Фурье со спектром непрерывных сигналов. Спектр непрерывного сигнала определяется преобразованием
- 48. Тогда спектр S( f ) такого сигнала будет равен интегралу с конечными пределами. (45) Проведем дискретизацию
- 49. В методе прямоугольников интеграл (3) заменяем следующей суммой (46) Выразим шаг дискретизации через частоту Найквиста Тогда
- 50. Сравним формулу (47) с выражением (36) для спектра дискретного сигнала. Мы видим, что формулы очень похожи.
- 51. Обычно нас интересует спектр, как для положительных значений частоты f > 0 ,так и для отрицательных
- 52. Чтобы сумме в выражении (51) придать вид ДПФ, сделаем замену индексов. В результате формула (51) примет
- 53. Заменим последовательность другой последовательностью по правилу. (53) В этом случае спектр сигнала (52) принимает вид (54)
- 54. (55) Отличие суммы (55) от настоящего ДПФ, приведенного в формуле (2), состоит в следующем. В настоящем
- 55. Разобьем этот интервал на две части. Рассмотрим сначала правую часть этого интервала (58) Интервал (58) содержится
- 56. Таким образом, мы получили формулу для вычисления половины спектра. Теперь рассмотрим левую часть интервала (57) (61)
- 57. Сумма (55) в этом случае примет вид (63) Последняя сумма в (63) является ДПФ, так как
- 59. Скачать презентацию




















































 Автоматизация парковок и паркингов. Альянс-Т. Г. Тула
Автоматизация парковок и паркингов. Альянс-Т. Г. Тула Аттестационная работа. Проектно-исследовательская деятельность по краеведению в начальных классах
Аттестационная работа. Проектно-исследовательская деятельность по краеведению в начальных классах Тема проекта: КАКАЯ ОНА, ПТИЦА СЧАСТЬЯ? Есть где-то Счастья птица, А мы живем и верим, Что счастье постучится Однажды в наши двери.
Тема проекта: КАКАЯ ОНА, ПТИЦА СЧАСТЬЯ? Есть где-то Счастья птица, А мы живем и верим, Что счастье постучится Однажды в наши двери.  Разбор по членам предложения Как устроен наш язык
Разбор по членам предложения Как устроен наш язык Тестовые задания для проведения итоговой аттестации
Тестовые задания для проведения итоговой аттестации Иновационные методы проектирования и производства корпусной мебели, как один из видов социокультурной практики
Иновационные методы проектирования и производства корпусной мебели, как один из видов социокультурной практики Борновское приближение. Быстрые и медленные частицы
Борновское приближение. Быстрые и медленные частицы Службова телефонна розмова: вимоги, композиція, мовні особливості
Службова телефонна розмова: вимоги, композиція, мовні особливості Квантовые компьютеры
Квантовые компьютеры Средства и способы ведения современного общевойскового боя
Средства и способы ведения современного общевойскового боя Металлы применяемые в строительстве
Металлы применяемые в строительстве Психотропные средства
Психотропные средства Программирование на языке C++. Символьные строки
Программирование на языке C++. Символьные строки Система МООДУС Модульная Объектно-Ориентированная Учебная Система
Система МООДУС Модульная Объектно-Ориентированная Учебная Система Формирование учетной политики в бухгалтерском учете Доцент, к.э.н. Зайцева Татьяна Львовна
Формирование учетной политики в бухгалтерском учете Доцент, к.э.н. Зайцева Татьяна Львовна Презентация Эволюционистская концепция происхождения культуры
Презентация Эволюционистская концепция происхождения культуры Презентация Французский классицизм 17 века
Презентация Французский классицизм 17 века Лазеры на центрах окраски
Лазеры на центрах окраски Устойчивая система. Ортопатия, ортодоксия, ортопраксия
Устойчивая система. Ортопатия, ортодоксия, ортопраксия Строчка прямого стежка и её варианты
Строчка прямого стежка и её варианты  Паломничество и святыни
Паломничество и святыни Презентация Порядок совершения таможенных операций в отношении товаров, перемещаемых через таможенную границу
Презентация Порядок совершения таможенных операций в отношении товаров, перемещаемых через таможенную границу  Әмирхан Еники. Тормыш юлы һәм иҗаты
Әмирхан Еники. Тормыш юлы һәм иҗаты Что такое ГТО
Что такое ГТО Поля коммутации
Поля коммутации  Палау
Палау Острые и хронические периодонтиты. Этиология
Острые и хронические периодонтиты. Этиология Понятие о девиации и аддикции. Аддиктивная личность. Виды и особенности аддиктивного поведения детей и подростков
Понятие о девиации и аддикции. Аддиктивная личность. Виды и особенности аддиктивного поведения детей и подростков