Содержание
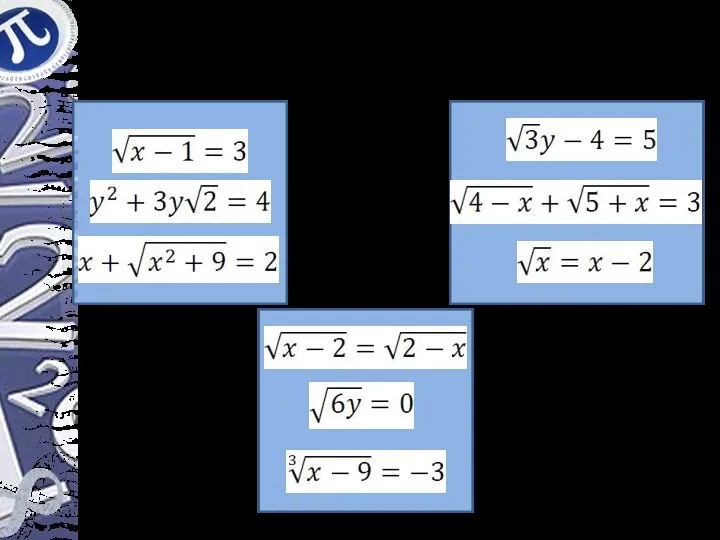
- 2. Выбрать иррациональное уравнение:
- 3. Иррациональные уравнения содержат радикалы. Чтобы избавиться от радикалов, необходимо возвести обе части уравнения в одну и
- 4. Алгоритм решения простейшего иррационального уравнения Возвести обе части уравнения в нужную степень. Решить полученное рациональное уравнение.
- 5. Решить иррациональное уравнение х2 –х-2=4 х2 –х - 6=0 х1=3 Проверка Ответ: 3; -2 х2=
- 6. Самостоятельная работа I III II IV
- 7. Устная работа Можно ли, не решая уравнений, сделать вывод о неразрешимости предложенных уравнений:
- 8. Методы решения иррациональных уравнений Введение новой переменной Исследование ОДЗ Умножение обеих частей уравнения на сопряженный множитель.
- 9. Методы решения иррациональных уравнений Использование ограниченности выражений, входящих в уравнение Использование свойств монотонности функций Функционально -
- 10. Пример. Решите уравнение: 1 способ. 2 способ.
- 11. Этот метод называется методом введения новой переменной. Примеры: После замены
- 12. Введение новой переменной Решить уравнение. Решение. Пусть , t – неотрицательное число, тогда имеем Отсюда, t1=2,
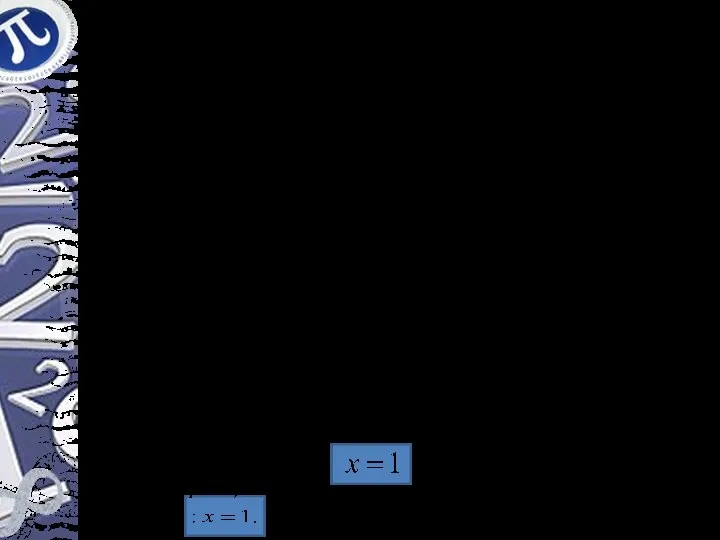
- 13. Решить уравнение Исследование ОДЗ Решение. Замечаем, что ОДЗ уравнения состоит из одной точки х=1. Проверкой убеждаемся,
- 14. Умножение обеих частей уравнения на сопряженный множитель Решить уравнение Решение. Умножим обе части уравнения на Получим,
- 15. Сведение уравнения к системе рациональных уравнений с помощью введения переменной Решить уравнение Решение. Положим Тогда u+v=3.
- 16. Выделение полного квадрата Решить уравнение Решение. Заметим, что Следовательно, имеем уравнение Данное уравнение равносильно совокупности двух
- 17. Использование ограниченности выражений, входящих в уравнение Решить уравнение Решение. Так как для любых значений х, то
- 18. Использование свойств монотонности функций Решить уравнение Решение. Если функция u(x) монотонна, то уравнение и(х) = А
- 20. Скачать презентацию


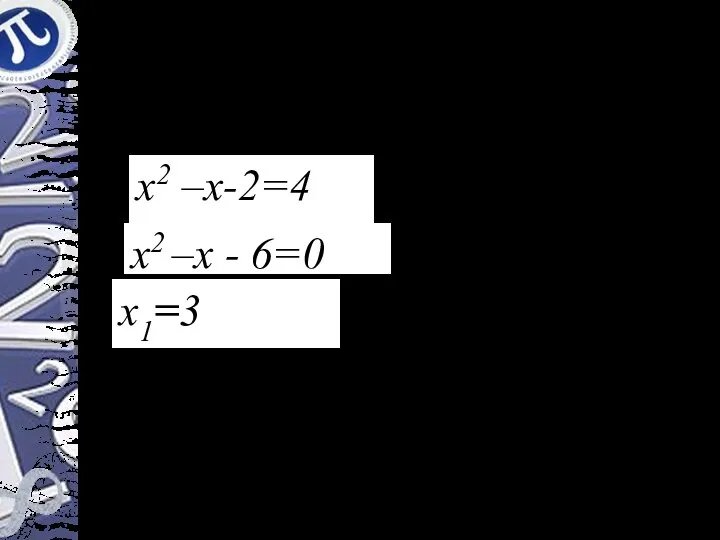












 Субъекты процедур банкротства
Субъекты процедур банкротства Аттестация в вопросах и ответах Из Письма Минобрнауки "Разъяснения по применению Порядка аттестации педагогических работ
Аттестация в вопросах и ответах Из Письма Минобрнауки "Разъяснения по применению Порядка аттестации педагогических работ Japanse Cultuur
Japanse Cultuur Політичні системи суспільства
Політичні системи суспільства Шпоночные соединения
Шпоночные соединения Как стать любимым тестировщиком у разработчика. Повышение качества взаимодействия программиста и тестировщика
Как стать любимым тестировщиком у разработчика. Повышение качества взаимодействия программиста и тестировщика Тема 2. «Теории эластичности спроса и предложения»
Тема 2. «Теории эластичности спроса и предложения» Государственная служба. Конфликт интересов
Государственная служба. Конфликт интересов High Gain InAs e-APDS with Excess Noise Factors Approaching a Solid State Photo-Multiplier
High Gain InAs e-APDS with Excess Noise Factors Approaching a Solid State Photo-Multiplier Производство ремонтно-строительных работ. Ремонт фундаментов, стен и перегородок зданий. (Тема 2.2)
Производство ремонтно-строительных работ. Ремонт фундаментов, стен и перегородок зданий. (Тема 2.2)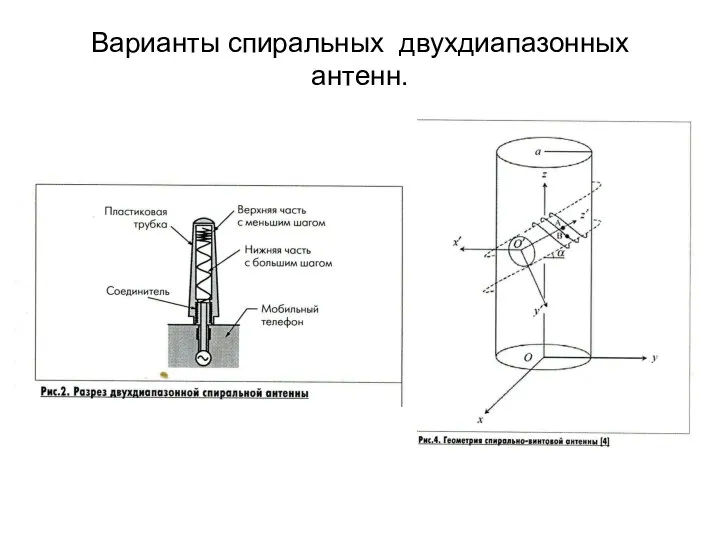 Антенны абонентских станций
Антенны абонентских станций Пробне ЗНО 2015
Пробне ЗНО 2015 Двойственный симплекс-метод
Двойственный симплекс-метод Жизненный цикл организации Петрова М. Зедеев А.
Жизненный цикл организации Петрова М. Зедеев А. Великобритания (Политическая система, образование, культура и традиции)
Великобритания (Политическая система, образование, культура и традиции) Презентация на тему "Физкультминутка для кистей рук" - скачать презентации по Педагогике
Презентация на тему "Физкультминутка для кистей рук" - скачать презентации по Педагогике Виды трансакционных издержек Астапова Настя Гмф1-2
Виды трансакционных издержек Астапова Настя Гмф1-2  Тест по правоведению Выполнили студенты 2-го курса Группы т-116с Ростовский Андрей и Вьюнкова Александра
Тест по правоведению Выполнили студенты 2-го курса Группы т-116с Ростовский Андрей и Вьюнкова Александра Современное музееведение
Современное музееведение ЛИТЕРАТУРНОЕ КРАЕВЕДЕНИЕ - презентация для начальной школы
ЛИТЕРАТУРНОЕ КРАЕВЕДЕНИЕ - презентация для начальной школы Услуги по защите окружающей среды Выполнила студентка ФТД-4 группа Т-103 Лепичева Наталия
Услуги по защите окружающей среды Выполнила студентка ФТД-4 группа Т-103 Лепичева Наталия Расчет прогиба. Железобетонные балки и плиты
Расчет прогиба. Железобетонные балки и плиты 6 класс. МХК.
6 класс. МХК. Презентация Качество непродовольственных товаров лекция
Презентация Качество непродовольственных товаров лекция Культура и быт народов севера
Культура и быт народов севера Нотариустың рәсімдеу жазбасы. Нотариалдық іс жүргізу тәртібі
Нотариустың рәсімдеу жазбасы. Нотариалдық іс жүргізу тәртібі Группа компаний «Метаком». Блоки вызова. Коммутаторы и разветвители. Блоки питания. Видеодомофоны. Ключи. Кнопки выхода. Замки
Группа компаний «Метаком». Блоки вызова. Коммутаторы и разветвители. Блоки питания. Видеодомофоны. Ключи. Кнопки выхода. Замки Языковая личность как объект лингвоперсонологии
Языковая личность как объект лингвоперсонологии