Содержание
- 2. Ідеальна модель і поверхневі стани Зонні енергетичні діаграми контактів метал-напівпровідник q ϕm - q (χ +
- 3. Збіднений шар Зонні енергетичні діаграми контактів метала з напівпровідниками n- і p- типів при різних зміщеннях.
- 4. Рівняння Пуасона: ∇2ϕ=-ρ/ε0εs Різкий несиметричний p-n перехід; Наближення різкої границі збідненого шару: (ρ≈qND при x W
- 5. Питома ємність збідненого шару Якщо концентрація ND постійна у всій області збідненого шару, то на графіку
- 6. Ефект Шотткі Енергетична діаграма системи метал-вакуум. Ефективна робота виходу при прикладанні зовнішнього електричного поля зменшується. Це
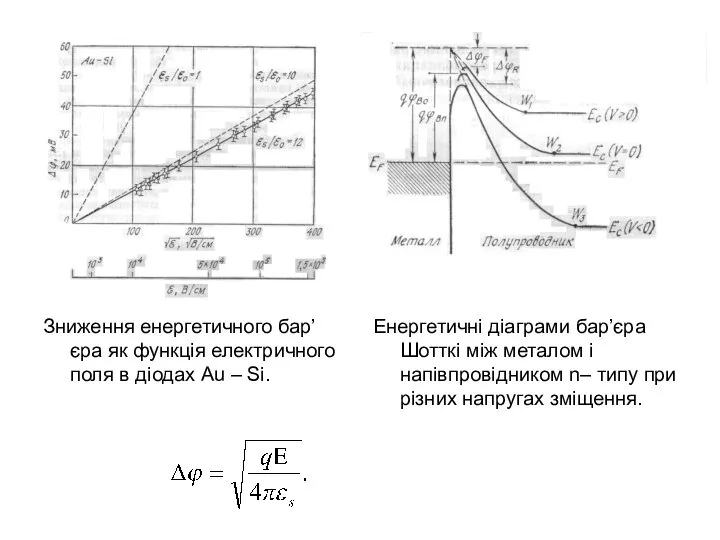
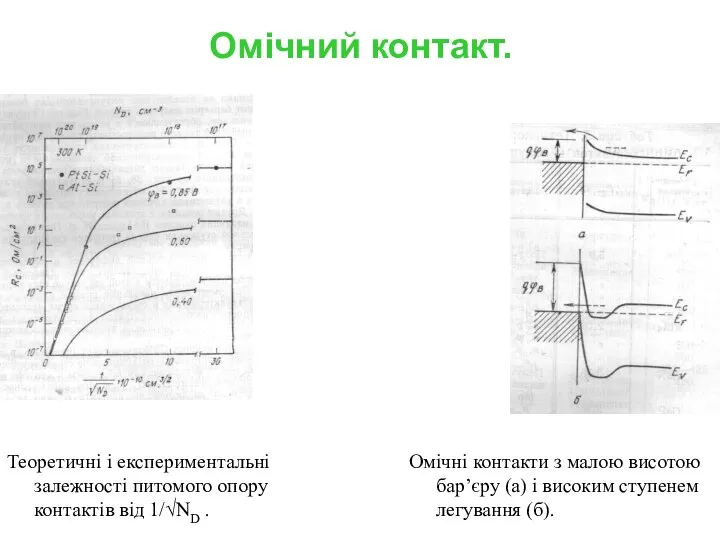
- 7. Зниження енергетичного бар’єра як функція електричного поля в діодах Au – Si. Енергетичні діаграми бар’єра Шотткі
- 8. Теорія процесів переносу заряда Чотири основні процеси переносу при прямому зміщенні. 1.Надбар’єрний переніс. 2. Квантовомеханічне тунелювання
- 9. 1. Теорія термоелектронної емісії. Припущення: 1. Висота бар’єру qϕBn набагато більша kT 2. Область, що визначає
- 10. 2. Дифузійна теорія Припущення: 1. Висота бар’єру qϕBn набагато більша kT шарі грає суттєву роль. 3.
- 11. Розподіл потенціалу в бар’єрі Шотткі: JSD сильніше залежить від напруги і менш чутлива до температури, ніж
- 12. 3. Термоемісійна- дифузійна теорія. Енергетична діаграма контакту з урахуванням ефекту Шотткі. qψ(x)– потенціальна енергія електрона, qϕ(x)
- 13. Якщо vD>>vR, то передекспоненційному члені залишається лише vR і справедлива теорія термоелектронної емісії. Якщо vD Остаточний
- 14. Ефективна постійна Річардсона Розрахункові значення ефективної постійної Річардсона як функціії електричного поля в бар’єрі метал-кремній.
- 15. 4. Тунельний струм Дві компоненти струму: термоелектронна і тунельна. n- фактор неідеальності. При V>>kT/q Тунельна компонента
- 16. Залежності густини струму насичення (а) и фактору неідеальності n (б) від концентрації легуючої домішки в діоді
- 17. 5. Інжекція неосновних носіїв. Енергетична діаграма епітаксійного бар’єру Шотткі. Рівняння неперервності: Рівняння густини струму для неосновних
- 18. Висота бар’єра Детальна енергетична діаграма контакту метал-напівпровідник – типу при наявності проміжного шару товщиною порядку міжатомних
- 19. Висота бар’єра Два припущення: 1.Товщина проміжного шару між металом і напівпровідником або дорівнює нулю, або порядку
- 20. Вирішуємо відносно ϕBn і отримуємо: де При εs≈10ε0, εi=ε0 і ND Якщо c1 і c3 можна
- 21. Два граничні випадки: 1. Якщо Ds → ∞ , то c2 → 0 і В цьому
- 22. Виміри висоти бар’єру. 1. Метод вольт-амперної характеристики Залежність густини струму в діодах W-Si і W-GaAs від
- 23. 2. Метод енергії активації. Залежність струму від температури в координатах, що використовуються для визначення висоти бар’єру.
- 24. 3. Метод вольт-фарадної характеристики Залежність 1/C2 від прикладеної напруги для діодів W-Si і W-GaAs. Напівпровідник з
- 25. Якщо концентрація ND постійна у всій області збідненого шару, то на графіку 1/C2 від V отримаємо
- 26. 4. Фотоелектричний метод. Принципова схема установки для фотоелектричних вимірювань (а) і енергетична діаграма процесів фотозбудження (б).
- 27. Теорія Фаулера. Залежність квантового виходу R від енергії фотона hν виражається формулою: де hν0=qϕBn - висота
- 28. Омічний контакт. Теоретичні і експериментальні залежності питомого опору контактів від 1/√ND . Омічні контакти з малою
- 29. Найбільш важливою характеристикою контакту є питомий опір при нульовому зміщенні 1. В контакті метал-напівпровідник з низьким
- 31. Скачать презентацию


























 Аппаратура для регистрации сейсмических событий.
Аппаратура для регистрации сейсмических событий.  הפעל בתצוגה מלאה בלבד!
הפעל בתצוגה מלאה בלבד! Культура Киевской Руси
Культура Киевской Руси Искусство рассказывает о красоте Земли 8 класс
Искусство рассказывает о красоте Земли 8 класс Исследование возможности использования «теплой» керамики при строительстве жилых зданий
Исследование возможности использования «теплой» керамики при строительстве жилых зданий Влияние иностранной культуры на культуру России
Влияние иностранной культуры на культуру России Презентация на тему "возрастные и индивидуальные особенности развития личности" - скачать презентации по Педагогике
Презентация на тему "возрастные и индивидуальные особенности развития личности" - скачать презентации по Педагогике Реестры государственных услуг и реестры муниципальных услуг
Реестры государственных услуг и реестры муниципальных услуг Функциональная анатомия соединений костей туловища и головы
Функциональная анатомия соединений костей туловища и головы  Презентация "Информационная система взаимодействия производственного планирования и учета затрат" - скачать презентации по
Презентация "Информационная система взаимодействия производственного планирования и учета затрат" - скачать презентации по  Почечное кровообращение и его регуляция
Почечное кровообращение и его регуляция Функционально-стоимостной анализ (ФСА). Сущность и сферы применения ФСА
Функционально-стоимостной анализ (ФСА). Сущность и сферы применения ФСА Страна Смешариков - презентация для начальной школы_
Страна Смешариков - презентация для начальной школы_ Эффективность применения пробиотика при технологическом стрессе у поросят-отъемышей. ООО СХП «Елизовский свинокомплекс»
Эффективность применения пробиотика при технологическом стрессе у поросят-отъемышей. ООО СХП «Елизовский свинокомплекс» Презентация узел связи RILO Москва
Презентация узел связи RILO Москва ЧЕМ КОРМИТЬ ПТИЦ ЗИМОЙ? 1 КЛАСС
ЧЕМ КОРМИТЬ ПТИЦ ЗИМОЙ? 1 КЛАСС Основные формы ФИДИК и OPBRC контрактов (Международная федерация инженеров-консультантов)
Основные формы ФИДИК и OPBRC контрактов (Международная федерация инженеров-консультантов) От решения о запуске до первой продажи. Основные этапы запуска интернет-магазина.
От решения о запуске до первой продажи. Основные этапы запуска интернет-магазина.  Тема 2 Общая классификация СЭД
Тема 2 Общая классификация СЭД Прямые выплаты на территории Забайкальского края. Фонд социального страхования РФ
Прямые выплаты на территории Забайкальского края. Фонд социального страхования РФ Выполнила: Студентка 5 группы 5 курса Факультета управления РГГУ Дарья Якадина Москва 2009. - презентация_
Выполнила: Студентка 5 группы 5 курса Факультета управления РГГУ Дарья Якадина Москва 2009. - презентация_ Среда распространения сигнала. (Лекция 1.5)
Среда распространения сигнала. (Лекция 1.5) Международные экономические организации в системе регулирования международной торговли
Международные экономические организации в системе регулирования международной торговли  Политическое сознание и политическое поведение
Политическое сознание и политическое поведение Порядок выбора объектов автоматизации
Порядок выбора объектов автоматизации Презентация на тему "МОДЕРНИЗАЦИЯ ОБРАЗОВАНИЯ" - скачать презентации по Педагогике
Презентация на тему "МОДЕРНИЗАЦИЯ ОБРАЗОВАНИЯ" - скачать презентации по Педагогике Презентация "Оптические иллюзии. Кажущиеся фигуры" - скачать презентации по МХК
Презентация "Оптические иллюзии. Кажущиеся фигуры" - скачать презентации по МХК ФГОС Классификация компетенций
ФГОС Классификация компетенций