Содержание
- 2. Определения Пусть дан ориентированный взвешенный граф G= с весовой функцией Весом пути называется сумма весов ребер,
- 3. Определения если существует путь из u в v
- 4. Определения Кратчайший путь из u в v – это любой путь p из u и v,
- 5. Варианты задач о кратчайшем пути Кратчайший путь из одной вершины: Дан взвешенный граф G= и начальная
- 6. Варианты задач о кратчайшем пути Кратчайший путь между парой вершин: Даны вершины u и v. Требуется
- 7. Варианты задач о кратчайшем пути Часто в задачах бывает необходимо найти не только кратчайший путь, но
- 8. Свойства кратчайших путей Лемма 1. (отрезки кратчайших путей являются кратчайшими) Пусть дан ориентированный взвешенный граф G=
- 9. Свойства кратчайших путей Следствие 1 Пусть дан ориентированный взвешенный граф G= с весовой функцией Рассмотрим кратчайший
- 10. Свойства кратчайших путей Лемма 2 Пусть дан ориентированный взвешенный граф G= с весовой функцией Пусть s∈V
- 11. Релаксация Для каждого ребра v∈V будем хранить некоторое число d[v], являющееся верхней оценкой веса кратчайшего пути
- 12. Релаксация Начальное значение оценки кратчайшего пути и массива π определяется следующим образом: Initialize(G,s)
- 13. Релаксация Релаксация ребра (u, v) состоит в следующем: Значение d[v] уменьшается до d[u]+w(u,v), если второе значение
- 14. Relax(u,v,w) If ( d[v]> d[u]+w(u,v)) d[v]=d[u]+w(u,v) π[v]=u В вершинах указаны оценки кратчайшего пути
- 15. Алгоритм Дейкстры Решает задачу о кратчайших путях из одной вершины s графа G= c весовой функцией
- 16. Алгоритм Дейкстры Алгоритм строит множество S вершин v, для которых кратчайшие пути до вершины s уже
- 17. Алгоритм Дейкстры Вершины, не лежащие в множестве S, хранятся в очереди с приоритетами, определяемыми значениями функции
- 19. Скачать презентацию









![Релаксация Для каждого ребра v∈V будем хранить некоторое число d[v], являющееся](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1372228/slide-10.jpg)

![Релаксация Релаксация ребра (u, v) состоит в следующем: Значение d[v] уменьшается](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1372228/slide-12.jpg)
![Relax(u,v,w) If ( d[v]> d[u]+w(u,v)) d[v]=d[u]+w(u,v) π[v]=u В вершинах указаны оценки кратчайшего пути](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1372228/slide-13.jpg)



 Сборная Новосибирской области по рыболовному спорту
Сборная Новосибирской области по рыболовному спорту РОЛЬ ЦВЕТА В ПОРТРЕТЕ
РОЛЬ ЦВЕТА В ПОРТРЕТЕ ФЕДЕРАЛЬНЫЙ ЗАКОН ОБ ОБЕСПЕЧЕНИИ ЕДИНСТВА ИЗМЕРЕНИЙ
ФЕДЕРАЛЬНЫЙ ЗАКОН ОБ ОБЕСПЕЧЕНИИ ЕДИНСТВА ИЗМЕРЕНИЙ Производство оптического бесцветного стекла
Производство оптического бесцветного стекла Створення системи деплойменту ігрових серверів
Створення системи деплойменту ігрових серверів От Йосиф Христофоров Хинов, Виолина Дин Нгуен и Сияна Тринх Нгуен Специалност – ИТ 40 Група
От Йосиф Христофоров Хинов, Виолина Дин Нгуен и Сияна Тринх Нгуен Специалност – ИТ 40 Група Презентация Федеральное собрание
Презентация Федеральное собрание  Нормативно-правовое регулирование фармацевтической деятельности. Классификация и структура аптечных организаций
Нормативно-правовое регулирование фармацевтической деятельности. Классификация и структура аптечных организаций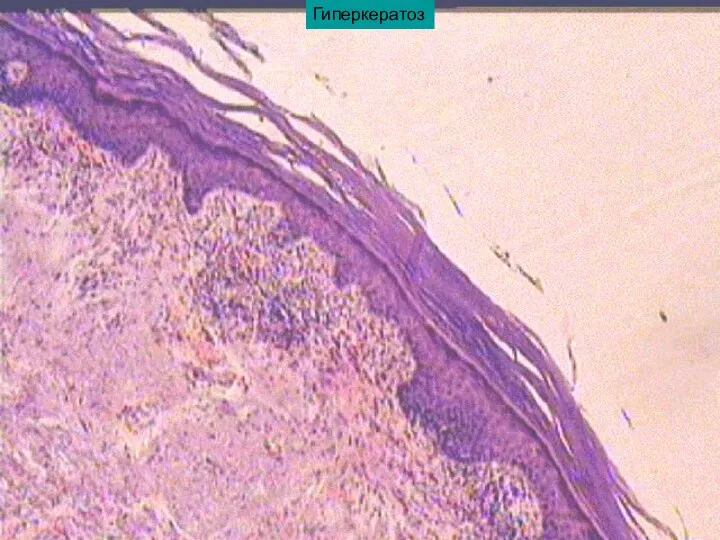 3 занятие_стом.ppt
3 занятие_стом.ppt «Поведение потребителей автомобилей» Бондарева Лидия Гавриш Кристина Житкова Екатерина Пономарева Виктория
«Поведение потребителей автомобилей» Бондарева Лидия Гавриш Кристина Житкова Екатерина Пономарева Виктория Презентация____
Презентация____ Технологии Internet
Технологии Internet Фитнес клуб Gym Style для всей семьи
Фитнес клуб Gym Style для всей семьи Философия Серебряного века
Философия Серебряного века Прикладное программное обеспечение
Прикладное программное обеспечение Кишечные простейшие
Кишечные простейшие  ОХРАНА ТРУДА ЖЕНЩИН
ОХРАНА ТРУДА ЖЕНЩИН Классификация осужденных
Классификация осужденных Презентация Особенности теории человеческого капитала
Презентация Особенности теории человеческого капитала Роль религии в жизни общества
Роль религии в жизни общества Гражданское общество и правовое государство. 9 класс
Гражданское общество и правовое государство. 9 класс Административные правоотношения
Административные правоотношения Баскетбол. История вида спорта
Баскетбол. История вида спорта Семиотика и синдромология заболеваний кишечника
Семиотика и синдромология заболеваний кишечника Инструменты оценки соискателей на позицию медицинского представителя (case studies)
Инструменты оценки соискателей на позицию медицинского представителя (case studies) Типы общества
Типы общества Классификация ассортимента и показателей качества бытовых холодильников
Классификация ассортимента и показателей качества бытовых холодильников Презентация Министерство Финансов
Презентация Министерство Финансов