Содержание
- 2. 1. Депланация незамкнутого тонкостенного сечения Рассмотрим тонкостенный стержень открытого профиля с произвольной формой сечения. При свободном
- 3. На рис. показано, что в результате поворота сечения и его депланации точка М переместилась в положение
- 4. На рисунке изображен поворот сечения на угол φ относительно полюса или центра кручения А (он также
- 5. z x Произведение r·ds=dω стоящее под знаком интеграла геометрически представляет собой удвоенную площадь элементарного треугольника с
- 6. Пример 1: Построить эпюру ω и найти депланацию для Ζ-образного сечения, если углы закручивания стержня изменяются
- 7. 2.Главные секториальные координаты Из теории изгиба стержней известно, что использование в поперечном сечении специально выбранной системы
- 8. Новые моменты инерции включающие новую секториальную координату ω и имеют следующие названия и размерность: Jzω —секториально-линейные
- 9. Механический смысл равенств, входящих в определение главных секториальных координат сечения легко понять, если условно принять, что
- 10. Преобразование секториальной координаты при изменении положения полюса. На рисунке изображены приращения секториальной площади dωΒ>0 и dωA>0
- 11. Техника определения главных секториальных координат. Для выполнения трех равенств можно распоряжаться тремя параметрами, от которых зависит
- 12. Так как у,z — это главные центральные оси сечения, то Jyz=0, Sz= 0, Sy= 0. Решая
- 13. Для нахождения положения точки М0 построим эпюру ωА при найденном центре кручения А и произвольном начале
- 14. Пример 2: Построить эпюру главных секториальных координат для Ζ-образного сечения, рассмотренного в примере 1. Решение: Построенную
- 15. Найдем теперь константу D по формуле Здесь интеграл по площади заменен суммой интегралов по дуге контура,
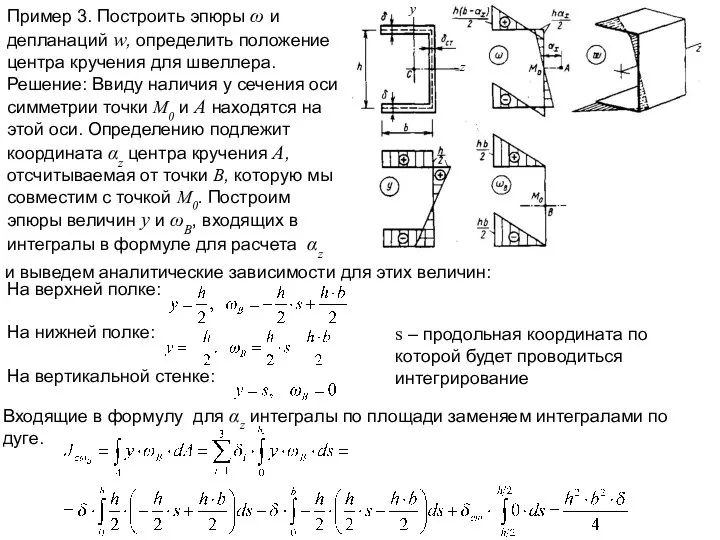
- 16. Пример 3. Построить эпюры ω и депланаций w, определить положение центра кручения для швеллера. Решение: Ввиду
- 18. Скачать презентацию
1. Депланация незамкнутого тонкостенного сечения
Рассмотрим тонкостенный стержень открытого профиля с
1. Депланация незамкнутого тонкостенного сечения
Рассмотрим тонкостенный стержень открытого профиля с
Наша задача — получить эти депланации в зависимости от угла закручивания φ(x).
Далее будем изображать лишь срединную поверхность стержня, а его поперечные сечения — в виде средних линий, без указания толщины δ. Положение произвольной точки М(x,s) в срединной поверхности зададим двумя координатами x и s, причем дуга s отсчитывается от некоторой начальной точки М0, подлежащей далее определению.
В точке М проведем плоскость, касательную к срединной поверхности, и обозначим перемещения точки в этой плоскости w и v, где v — перемещение в тангенциальном к контуру сечения направлении.
z
x
x
На рис. показано, что в результате поворота сечения и его депланации
На рис. показано, что в результате поворота сечения и его депланации
dx
Знак минус поставлен потому, что приращение перемещения (dv/dz)dz направлено в сторону, противоположную направлению отсчета координаты s.
После сокращения на ds и dx получим искомое соотношение:
Условие отсутствия сдвигов в срединной поверхности
Примем гипотезу о том, что вдоль всего стержня установлены диафрагмы, которые, не сопротивляясь депланации, обеспечивают при закручивании стержня поворот каждого поперечного сечения как жесткого диска.
(гипотеза неизгибаемости контура поперечного сечения)
На рисунке изображен поворот сечения на угол φ относительно полюса или
На рисунке изображен поворот сечения на угол φ относительно полюса или
Подставляя в условие отсутствия сдвигов в срединной поверхности и обозначая дифференцирование по координате x через (dφ/dx)=φ', получаем
Интегрируя данное выражение по дуге s, получим:
где w0 — перемещение начальной точки М0.
z
x
Произведение r·ds=dω стоящее под знаком интеграла геометрически представляет собой удвоенную площадь
z
x
Произведение r·ds=dω стоящее под знаком интеграла геометрически представляет собой удвоенную площадь
закон изменения перемещения w вдоль контура сечения вследствие депланации сечения в срединной поверхности.
Так как w пропорционально ω, то говорят, что в тонкостенном стержне открытого профиля депланация происходит по закону cекториальных площадей. Степень развития депланаций сечения зависит от относительного угла закручивания φ'. С крутящим моментом φ' связан соотношением изученным ранее. Между положением точки на дуге s и площадью ω существует однозначное соответствие. Поэтому секториальную площадь ω называют секториальной координатой точки. Если ее линейные координаты х и у имеют размерность [м], то размерность ω будет [м2].
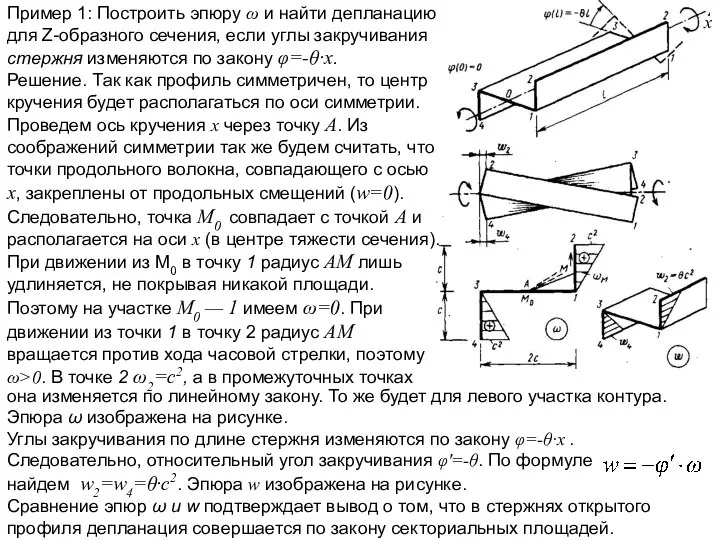
Пример 1: Построить эпюру ω и найти депланацию для Ζ-образного сечения,
Пример 1: Построить эпюру ω и найти депланацию для Ζ-образного сечения,
Решение. Так как профиль симметричен, то центр кручения будет располагаться по оси симметрии. Проведем ось кручения х через точку А. Из соображений симметрии так же будем считать, что точки продольного волокна, совпадающего с осью x, закреплены от продольных смещений (w=0). Следовательно, точка M0 совпадает с точкой А и располагается на оси x (в центре тяжести сечения). При движении из M0 в точку 1 радиус AM лишь удлиняется, не покрывая никакой площади. Поэтому на участке M0 — 1 имеем ω=0. При движении из точки 1 в точку 2 радиус AM вращается против хода часовой стрелки, поэтому ω>0. В точке 2 ω2=с2, а в промежуточных точках
она изменяется по линейному закону. То же будет для левого участка контура. Эпюра ω изображена на рисунке.
Углы закручивания по длине стержня изменяются по закону φ=-θ·x . Следовательно, относительный угол закручивания φ'=-θ. По формуле найдем w2=w4=θ·c2. Эпюра w изображена на рисунке.
Сравнение эпюр ω и w подтверждает вывод о том, что в стержнях открытого профиля депланация совершается по закону секториальных площадей.
x
2.Главные секториальные координаты
Из теории изгиба стержней известно, что использование в поперечном
2.Главные секториальные координаты
Из теории изгиба стержней известно, что использование в поперечном
Составим таблицу, симметричную относительно главной диагонали, которую назовем «матрицей моментов инерции»:
Здесь внедиагональные элементы матрицы J представляют интегралы от произведения координат, а элементы на главной диагонали — интегралы от их квадратов:
Новые моменты инерции включающие новую секториальную координату ω и имеют следующие
Новые моменты инерции включающие новую секториальную координату ω и имеют следующие
Jzω —секториально-линейные моменты инерции площади сечения, м5;
Jω — секториальный момент инерции сечения, м6.
Координаты называются главными, если в матрице моментов инерции J все внедиагональные элементы равны нулю.
Следовательно, главные секториальные координаты должны быть подчинены условиям:
Кроме того, по аналогии с понятием центральных осей, которые проходят через центр масс, в котором, в свою очередь, статические моменты равны нулю, потребуем, чтобы эпюра ω обращала аналогичный интеграл в ноль:
Координаты ω, удовлетворяющие данным равенствам, называют главными секториальными координатами сечения.
Механический смысл равенств, входящих в определение главных секториальных координат сечения легко
Механический смысл равенств, входящих в определение главных секториальных координат сечения легко
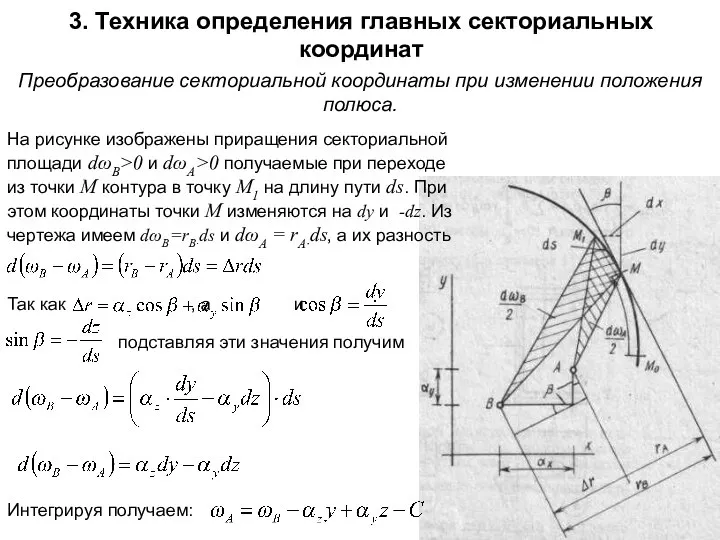
Преобразование секториальной координаты при изменении положения полюса.
На рисунке изображены приращения
Преобразование секториальной координаты при изменении положения полюса.
На рисунке изображены приращения
Так как , а и
подставляя эти значения получим
Интегрируя получаем:
3. Техника определения главных секториальных координат
Техника определения главных секториальных координат.
Для выполнения трех равенств можно распоряжаться
Техника определения главных секториальных координат.
Для выполнения трех равенств можно распоряжаться
z
αy
αz
z
где С — произвольная постоянная.
Для определения координат истинного центра кручения А зададимся вначале произвольной точкой В, пользуясь которой, как центром кручения при произвольном начале отсчета М1 построим эпюру ωΒ. Пусть αy и αz —координаты точки А по отношению к точке В. Ранее показано, что ωΑ и ωВ связаны равенством
Подставляя выражения для ωA в условия равенства линейно-секториальных момента нулю, придем к системе уравнений относительно αy и αz:
Так как у,z — это главные центральные оси сечения, то Jyz=0,
Так как у,z — это главные центральные оси сечения, то Jyz=0,
Решая имеем формулы для координат точки А:
Интегралы представляют собой рассмотренные ранее моменты
Раскрывая скобки и учитывая, что интеграл суммы равен сумме интегралов
Для нахождения положения точки М0 построим эпюру ωА при найденном центре
Для нахождения положения точки М0 построим эпюру ωА при найденном центре
Подставив данное выражение в условие равенство нулю статического момента, получим
отсюда
Вычитая D из ординат эпюры ωА, получаем эпюру главных секториальных координат. При этом может образоваться не одна нулевая точка. Любая из ниx может быть принята в качестве М0.
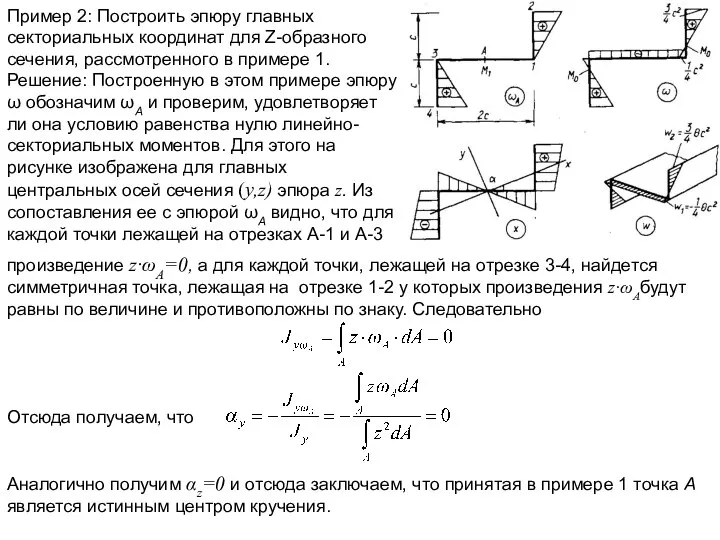
Пример 2: Построить эпюру главных секториальных координат для Ζ-образного сечения, рассмотренного
Пример 2: Построить эпюру главных секториальных координат для Ζ-образного сечения, рассмотренного
Решение: Построенную в этом примере эпюру ω обозначим ωА и проверим, удовлетворяет ли она условию равенства нулю линейно-секториальных моментов. Для этого на рисунке изображена для главных центральных осей сечения (у,z) эпюра z. Из сопоставления ее с эпюрой ωА видно, что для каждой точки лежащей на отрезках A-1 и А-3
произведение z·ωА=0, а для каждой точки, лежащей на отрезке 3-4, найдется симметричная точка, лежащая на отрезке 1-2 у которых произведения z·ωАбудут равны по величине и противоположны по знаку. Следовательно
Отсюда получаем, что
Аналогично получим αz=0 и отсюда заключаем, что принятая в примере 1 точка А является истинным центром кручения.
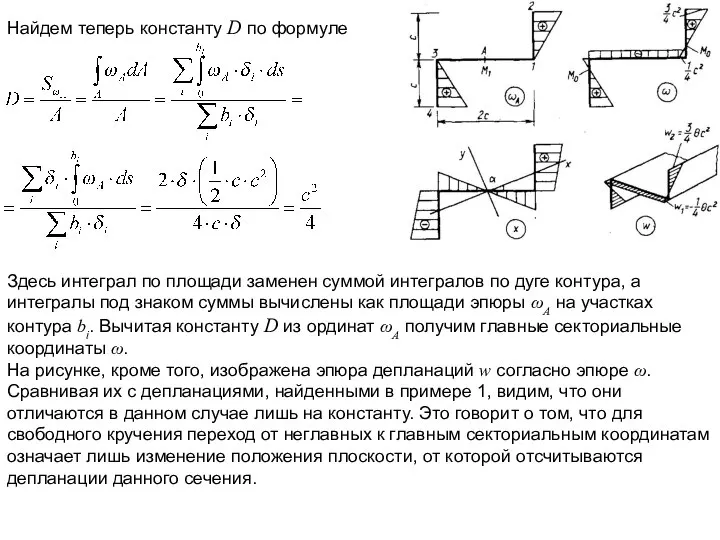
Найдем теперь константу D по формуле
Здесь интеграл по площади заменен
Найдем теперь константу D по формуле
Здесь интеграл по площади заменен
На рисунке, кроме того, изображена эпюра депланаций w согласно эпюре ω. Сравнивая их с депланациями, найденными в примере 1, видим, что они отличаются в данном случае лишь на константу. Это говорит о том, что для свободного кручения переход от неглавных к главным секториальным координатам означает лишь изменение положения плоскости, от которой отсчитываются депланации данного сечения.
Пример 3. Построить эпюры ω и депланаций w, определить положение центра
Пример 3. Построить эпюры ω и депланаций w, определить положение центра
Решение: Ввиду наличия у сечения оси симметрии точки M0 и А находятся на этой оси. Определению подлежит координата αz центра кручения А, отсчитываемая от точки В, которую мы совместим с точкой M0. Построим эпюры величин у и ωB, входящих в интегралы в формуле для расчета αz
На верхней полке:
На нижней полке:
На вертикальной стенке:
s – продольная координата по которой будет проводиться интегрирование
Входящие в формулу для αz интегралы по площади заменяем интегралами по дуге.
и выведем аналитические зависимости для этих величин:
y
z










 Единая школьная карта
Единая школьная карта Технологии разработки ПО. Основные понятия и определения
Технологии разработки ПО. Основные понятия и определения НОВАЯ ЭКОНОМИЧЕСКАЯ АССОЦИАЦИЯ ВТОРОЙ РОССИЙСКИЙ ЭКОНОМИЧЕСКИЙ КОНГРЕСС БОРЬБА С УКЛОНЕНИЕМ ОТ УПЛАТЫ НАЛОГОВ И «НАЛОГОВЫМИ
НОВАЯ ЭКОНОМИЧЕСКАЯ АССОЦИАЦИЯ ВТОРОЙ РОССИЙСКИЙ ЭКОНОМИЧЕСКИЙ КОНГРЕСС БОРЬБА С УКЛОНЕНИЕМ ОТ УПЛАТЫ НАЛОГОВ И «НАЛОГОВЫМИ  CSS (Cascading Style Sheets)
CSS (Cascading Style Sheets) құндылық
құндылық Мохандас Карамчанд Ганди
Мохандас Карамчанд Ганди «Есть такая профессия – ученик»
«Есть такая профессия – ученик» Реабилитация. Возмещение вреда
Реабилитация. Возмещение вреда Общие сведения о языке программирования Паскаль
Общие сведения о языке программирования Паскаль Заболевания щитовидной железы
Заболевания щитовидной железы Электро Механик
Электро Механик Роспись яиц
Роспись яиц Презентация Социально-обеспечительные правоотношения
Презентация Социально-обеспечительные правоотношения  «TIS-Трудозатраты» Система учета занятости сотрудников. - презентация
«TIS-Трудозатраты» Система учета занятости сотрудников. - презентация умножение и деление на 8 - презентация для начальной школы
умножение и деление на 8 - презентация для начальной школы Web-программирование. Лекция 5. python 3 (часть 2)
Web-программирование. Лекция 5. python 3 (часть 2) Презентация "Макроэкономическая нестабильность и ее основные проявления" - скачать презентации по Экономике
Презентация "Макроэкономическая нестабильность и ее основные проявления" - скачать презентации по Экономике Стратегии тестирования
Стратегии тестирования «Закрепление внетабличного деления и умножения» Математика, 3 класс Учитель начальных классов Симбирева Дарья Викторовна, ГБОУ
«Закрепление внетабличного деления и умножения» Математика, 3 класс Учитель начальных классов Симбирева Дарья Викторовна, ГБОУ  Диаграммы классов. Объектно- ориентированное программирование. (Лекция 5)
Диаграммы классов. Объектно- ориентированное программирование. (Лекция 5) Комплексное оснащение предприятий ресторанного бизнеса на примере овощерезки Robot Coupe CL 50
Комплексное оснащение предприятий ресторанного бизнеса на примере овощерезки Robot Coupe CL 50 Христианская апологетика и история
Христианская апологетика и история Сервис Фото для участников MyWeb Фотохостинг на MyWeb http://myweb.kz/
Сервис Фото для участников MyWeb Фотохостинг на MyWeb http://myweb.kz/ Прогнозирование денежного потока инвестиционного проекта
Прогнозирование денежного потока инвестиционного проекта  Анализ алгоритмов. (Лекция 16)
Анализ алгоритмов. (Лекция 16) The military factor in contemporary international relation
The military factor in contemporary international relation Описание слайда:
Методики определения потребности в лекарственных средствах.
Описание слайда:
Методики определения потребности в лекарственных средствах. ЗАЩИТА АНАЛИТИЧЕСКОГО ОТЧЁТА Юдиной Ирины Николаевны воспитатель ГПД
ЗАЩИТА АНАЛИТИЧЕСКОГО ОТЧЁТА Юдиной Ирины Николаевны воспитатель ГПД