Содержание
- 2. молекулярная динамика и метод Монте-Карло неэмпирическая квантовая химия полуэмпирическая квантовая химия квантовая статистическая механика молекулярная механика
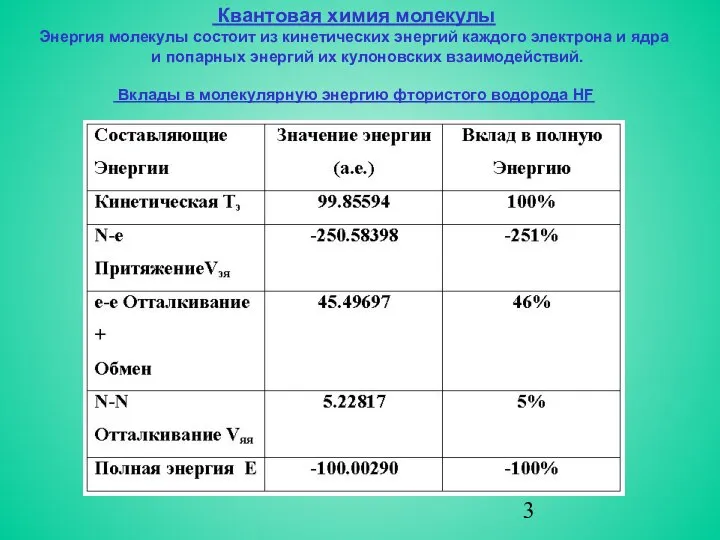
- 3. Квантовая химия молекулы Энергия молекулы состоит из кинетических энергий каждого электрона и ядра и попарных энергий
- 4. Основное уравнение молекулярной квантовой химии - независящее от времени нерелятивистское уравнение Шредингера: Н Ψ ({r, R})
- 5. Приближение Борна-Оппенгеймера Электрон-ядерное взаимодействие Vэя значительно и пренебречь им нельзя. Hмол зависит от координат электронов и
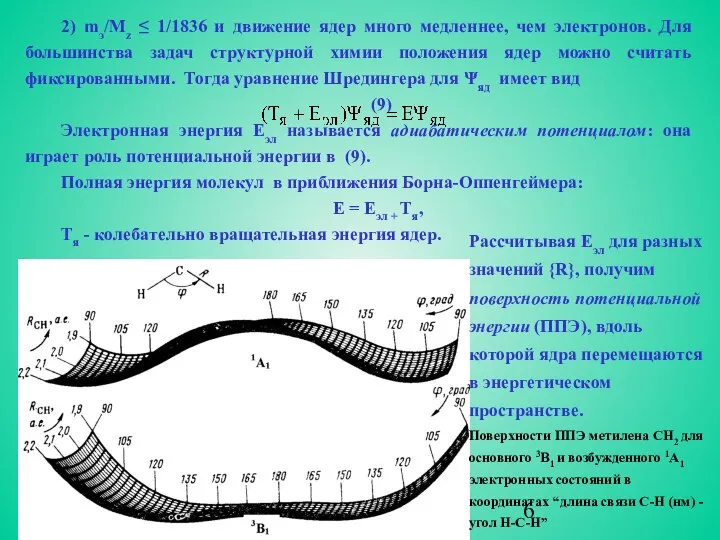
- 6. 2) mэ/Mz ≤ 1/1836 и движение ядер много медленнее, чем электронов. Для большинства задач структурной химии
- 7. Молекулярная структура Ядерная конфигурация молекулы стабильна относительно малых колебаний ядер и характеризует молекулярную структуру. Топология ППЭ
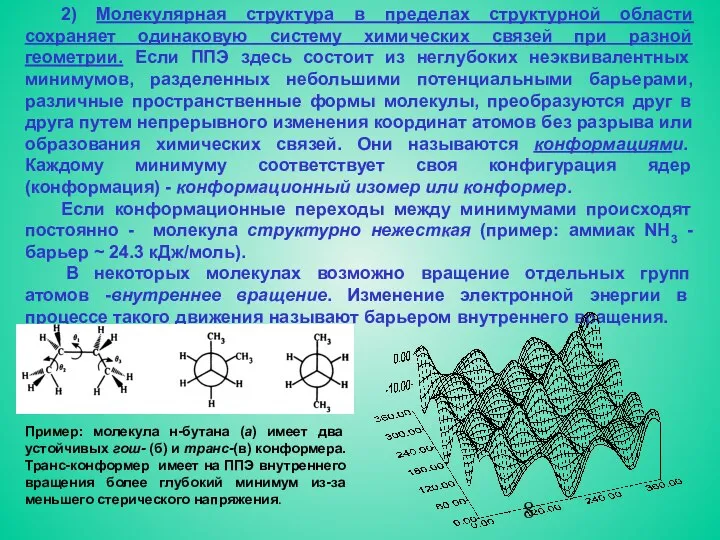
- 8. 2) Молекулярная структура в пределах структурной области сохраняет одинаковую систему химических связей при разной геометрии. Если
- 9. Энергии вращательных барьеров (ккал/моль) После символа // указан базис, в котором была оптимизирована геометрия. Молекулярная структура
- 10. 2.3 Метод Хартри-Фока для молекул Зафиксировав ядерную конфигурацию, для анализа электронного поведения молекул достаточно рассматривать только
- 11. Полная ХФ энергия молекулы с замкнутыми оболочками (2.11) Замечания. 1) В минимизации энергии участвуют только занятые
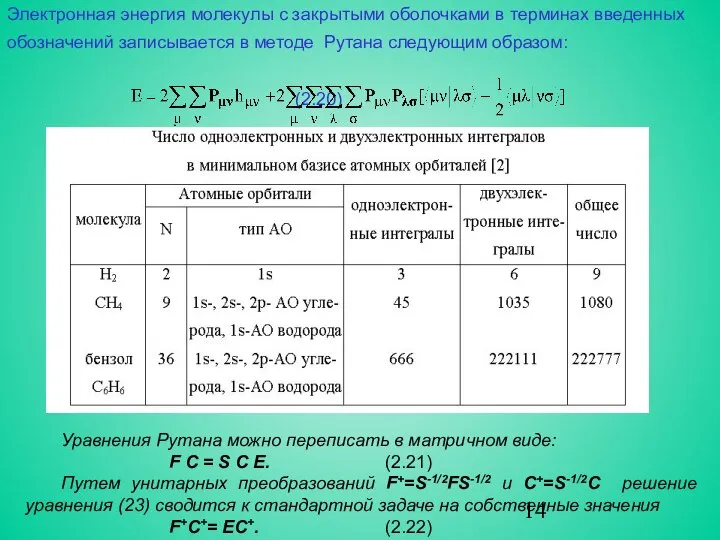
- 12. Приближение МО ЛКАО. Уравнения Рутана Уравнения Хартри-Фока для молекул Численное решение МО электрона, который находится в
- 13. (2.15) (2.16) (2.17) (2.18) Еμ - одно из решений секулярного уравнения Удобно ввести матрицу зарядов- порядков
- 14. Электронная энергия молекулы с закрытыми оболочками в терминах введенных обозначений записывается в методе Рутана следующим образом:
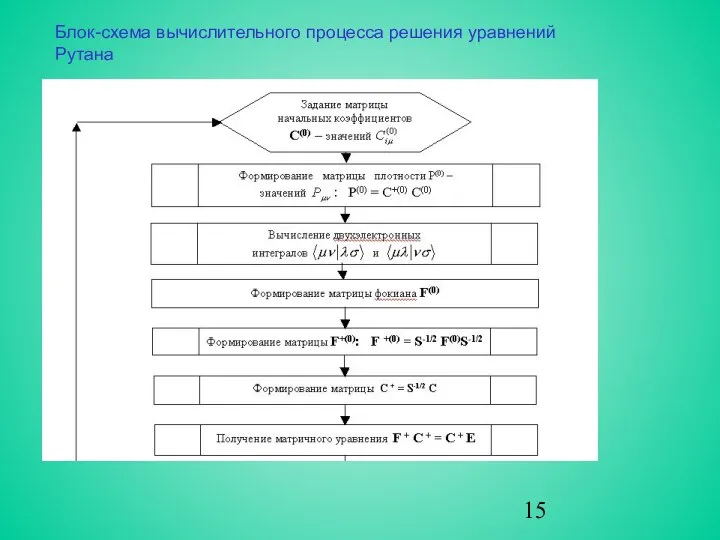
- 15. Блок-схема вычислительного процесса решения уравнений Рутана
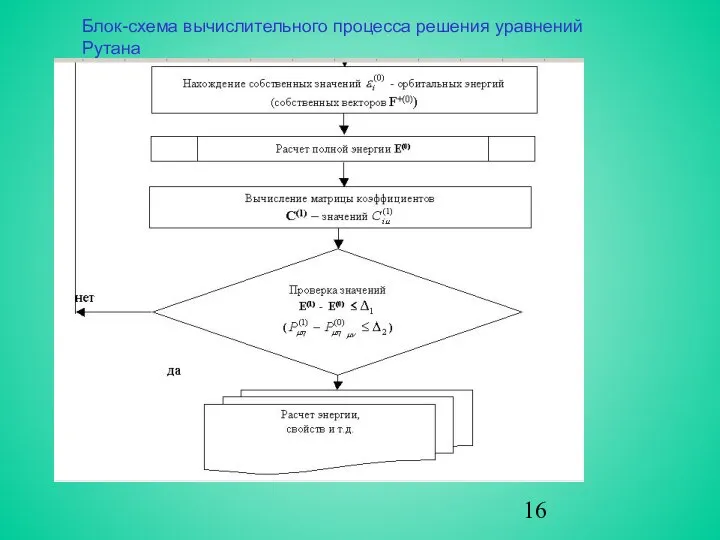
- 16. Блок-схема вычислительного процесса решения уравнений Рутана
- 17. Из-за наличия самосогласованного поля уравнения ХФ нелинейны: решения можно получить, лишь задав некоторый потенциал, обусловленный распределением
- 18. Многоэлектронная волновая функция и энергии состояний, получаемые с помощью метода Рутана (и с помощью метода Хартри-Фока
- 19. 4. Ограничения метода Хартри-Фока В ряде молекулярных задач, решаемых методом ХФ, проявляется так называемая "дилемма симметрии".
- 21. Скачать презентацию











 Спорт во мне
Спорт во мне Демедюк Лілія Мефодіївна- заступник директора з навчально-виховної роботи ЗОШ І-ІІ ст.села Козлів
Демедюк Лілія Мефодіївна- заступник директора з навчально-виховної роботи ЗОШ І-ІІ ст.села Козлів Конст право 11.pptx
Конст право 11.pptx Аналитика: каналы и инструменты
Аналитика: каналы и инструменты ВВС - Тема 2 - к лекции 24.09.2019
ВВС - Тема 2 - к лекции 24.09.2019 Святые и святость
Святые и святость Управление персоналом. Сущность, стратегия, стили управления персоналом. Лекция 4
Управление персоналом. Сущность, стратегия, стили управления персоналом. Лекция 4 О мероприятиях по реализации государственной социальной политики
О мероприятиях по реализации государственной социальной политики The second of February, Thursday
The second of February, Thursday  Тема 3.1: Организация и техника операций в торговле готовой продукцией. Особенности организации и техники по поставке машинотех
Тема 3.1: Организация и техника операций в торговле готовой продукцией. Особенности организации и техники по поставке машинотех Презентация Экологическое страхование
Презентация Экологическое страхование Операторы управления
Операторы управления Кодирование информации
Кодирование информации  Род Сoxiella. Сoxiella burnetii. Q-лихорадка. Название «Q-лихорадка» (от англ. queri - неясный) предложил Э. Деррик, впервые описавший заболевани
Род Сoxiella. Сoxiella burnetii. Q-лихорадка. Название «Q-лихорадка» (от англ. queri - неясный) предложил Э. Деррик, впервые описавший заболевани Жидкоструйные смесительные сопла сита и ситовой анализ
Жидкоструйные смесительные сопла сита и ситовой анализ Стратегия «Казахстан-2050». Новый политический курс состоявшегося государства
Стратегия «Казахстан-2050». Новый политический курс состоявшегося государства Психофізіологічна діагностика у спорті
Психофізіологічна діагностика у спорті МОУ «Крутинская гимназия» Словосочетание в предложении Учитель : Вершинина Т.А
МОУ «Крутинская гимназия» Словосочетание в предложении Учитель : Вершинина Т.А Хочу знать все! - презентация для начальной школы
Хочу знать все! - презентация для начальной школы Урок №31 (112) Тест «Единицы длины»
Урок №31 (112) Тест «Единицы длины»  Рационализация размещения товара на складе на примере предприятия ООО «Гекса – нетканые материалы»
Рационализация размещения товара на складе на примере предприятия ООО «Гекса – нетканые материалы» Определение предмета статистики в широком и узком смысле. Система правовой статистики.
Определение предмета статистики в широком и узком смысле. Система правовой статистики. Аттестационная работа. Программа внеурочной деятельности Пермский край – мой родной край
Аттестационная работа. Программа внеурочной деятельности Пермский край – мой родной край 5S on technical workshop. Бережливое производство
5S on technical workshop. Бережливое производство Антифосфолипидный синдром
Антифосфолипидный синдром Цвет как средство выражения. Теплые и холодные цвета
Цвет как средство выражения. Теплые и холодные цвета Города 1 и 2 уровня
Города 1 и 2 уровня ВКР: Разработка программного модуля проверки АРМ разработчика в среде Navisworks
ВКР: Разработка программного модуля проверки АРМ разработчика в среде Navisworks