Линейный Гармонический осциллятор в квантовой механике

обоснование и развитие.
Вспомним прежде всего, как в классической физике следует рассматривать колебания гармонического осциллятора. На рис. 27.2 изображен график потенциальной энергии U осциллятора U= kx2/2. На этом же графике показано значение полной энергии E частицы. Точкам В и С на графике U(x) соответствуют наибольшие отклонения частицы от положения равновесия, когда скорость частицы обращается в нуль и ее полная энергия

Рис. 27.2

становится равной потенциальной:
при υ = 0 .

(26.19)

(26.20)

зрения совершенно очевидно, что частица при своих колебаниях не может выйти за пределы области (-А, А).

Амплитуда А колебаний осциллятора определяется запасом его
полной энергии Е:

(26.21)

Такой выход означал бы, что потенциальная энергия U становится большей, чем полная энергия E частицы: U > E, что соответствует бессмысленному выводу об отрицательной кинетической энергии, т. е. о мнимой скорости. Если mυ2/2 < 0, то υ — мнимая величина!

мы должны будем учесть волновые свойства частицы, запертой внутри потенциальной ловушки, имеющей форму параболы (см. рис. 27.3). В квантовой механике соотношения неопределенностей приводят к принципиально новому результату: полная энергия гармонического осциллятора и амплитуда его колебаний не могут быть равны нулю. В самом деле, если частица «заперта» в области Δх ≈ А, то согласно П.Н. Δрх ≈ /А, и импульс р частицы не может быть равен нулю. Как показано ранее,

При этом

полная энергия Е удовлетворяет соотношению

(26.22)

Сравнивая (26.22) с (26.20) и исключив амплитуду А, имеем
.

нулевой энергией осциллятора.

(26.23)

Нулевая энергия осциллятора определяется только его собственной частотой v. Ее невозможно отнять у частицы никаким охлаждением, она сохранилась бы и при температуре абсолютного нуля. Нулевой энергии соответствуют некоторые «нулевые колебания» квантового осциллятора.
Существование нулевой энергии подтверждено экспериментально в явлении рассеяния света кристаллами при сверхнизких температурах. Рассеяние света в кристаллах происходит на тепловых колебаниях, которые совершают атомы, молекулы или ионы, расположенные в узлах кристаллической решетки. С классической точки зрения интенсивность рассеянного света должна убывать до нуля с уменьшением температуры до нуля, ибо

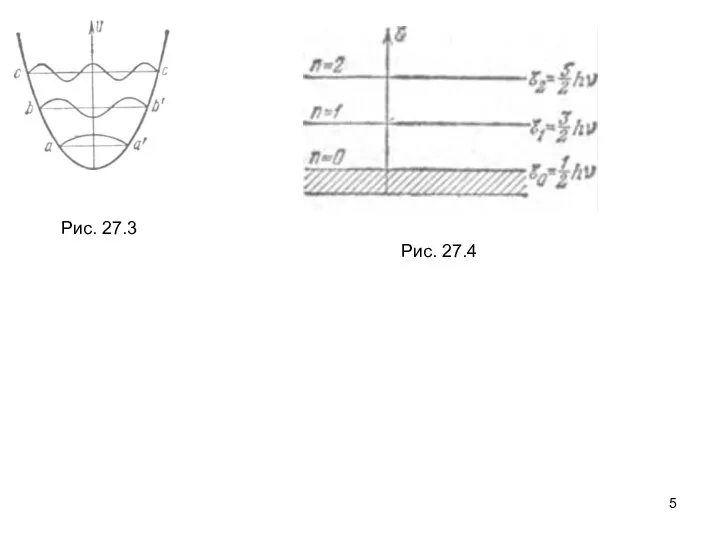
Опыты показали, что при уменьшении температуры интенсивность света, рассеянного кристаллами, стремится к некоторому предельному значению, которое не убывает при дальнейшем охлаждении кристалла. Результаты опытов показали, что при Т→0 у частиц, расположенных в узлах решетки, сохраняются некоторые «нулевые колебания», на которых и происходит рассеяние света. «Нулевым колебаниям» соответствует нулевая энергия атомных осцилляторов.

Наличие нулевой энергии является характерным признаком любой системы частиц, рассматриваемой в квантовой механике. При температурах, близких к абсолютному нулю, любое вещество находится в кристаллическом состоянии и его атомы (молекулы или ионы) ведут себя как некоторые колеблющиеся осцилляторы.

если давление не превышает 2,53 МПа. Это объясняется, во-первых, тем, что у гелия частота колебаний атомов достаточно велика, ибо мала масса атома . Поэтому у гелия нулевая энергия hv/2 имеет сравнительно
большую величину. С другой стороны, силы взаимодействия между атомами гелия малы, ибо у них электронные оболочки с двумя электронами полностью «застроены». В итоге атомы гелия при Т→0 находятся в интенсивном движении, и гелий при относительно небольших давлениях остается жидким и при Т→0. Поскольку причиной этого является квантовый эффект

частицы в этом случае ограничено потенциальной кривой параболического типа U = mω2х2/2 (рис. 26.3). Как и в случае частицы, «запертой» в прямоугольном ящике, наличие потенциальной ловушки параболического типа приводит к дискретному набору энергий частицы. Квантованные значения энергии осциллятора будут определяться тем, что на эффективной длине 2Aэфф = аа', b'b’, . . . укладывается нечетное число полуволн де Бройля.

Рис. 26.3

Введем эффективную длину волны де Бройля:
, (26.24)
где рэфф — эффективный импульс, связанный с энергией так, как будто потенциальная ловушка отсутствует и движение совершенно свободно:

эффективной амплитуде Aэфф укладывается нечетное число четвертей эффективных длин волн де Бройля: (26.26)

Подставив (26.26) в (26.20), получим
Е = (2n + 1 )2 mω2λ2 эфф/32. (26.27)
Перемножая (26.25) и (27.27), исключим λэфф и найдем дискретные энергетические уровни линейного гармонического осциллятора:
В квантовой механике при строгом подходе, основанном на решении уравнения Шредингера, получается следующее выражение для возможных энергий осциллятора:
E = (n + 1/2)hv, где n = 0,1,2,… (26.28)

систему равноотстоящих друг от друга значений энергии (рис. 26.4). Грубый расчет, приведенный выше, привел к правильной зависимости энергии линейного гармонического осциллятора от его частоты v и к правильному характеру зависимости En от n.

Рис. 26.4

существенному отличию от классического рассмотрения. Оказывается, что можно обнаружить частицу за пределами дозволенной области ⏐x⏐≤ A, т. е. за точками С и В на рис. 26.2. Как нам известно, это означает пребывание частицы там, где ее полная энергия Е меньше потенциальной энергии. Однако благодаря волновым свойствам частиц и принципу неопределенностей обнаружение частицы за пределами классически дозволенной области оказывается возможным. Подробнее мы рассмотрим причину этого в следующем параграфе.

http://portal.tpu.ru/departments/head/methodic/standart
Работы выпускные квалификационные, проекты и работы курсовые. Структура и правила оформления. СТО ТПУ 2.5.01-2006