Содержание
- 2. Вначале рассмотрим случай, когда частица с массой т движется с постоянной скоростью υ вдоль некоторого направления,
- 3. Здесь E и p — энергия и импульс частицы, i — мнимая единица (т. е. i2=
- 4. на оси х становится совершенно неопределенным. Об этом же говорит одинаковая вероятность обнаружить частицу во всех
- 5. Рассмотрим теперь микроскопическую частицу, движение которой вдоль оси х ограничено следующим образом. От начала координат x
- 6. Разумеется, таких ям практически не существует. Однако при изучении электропроводности металлов мы пользуемся представлением o том,
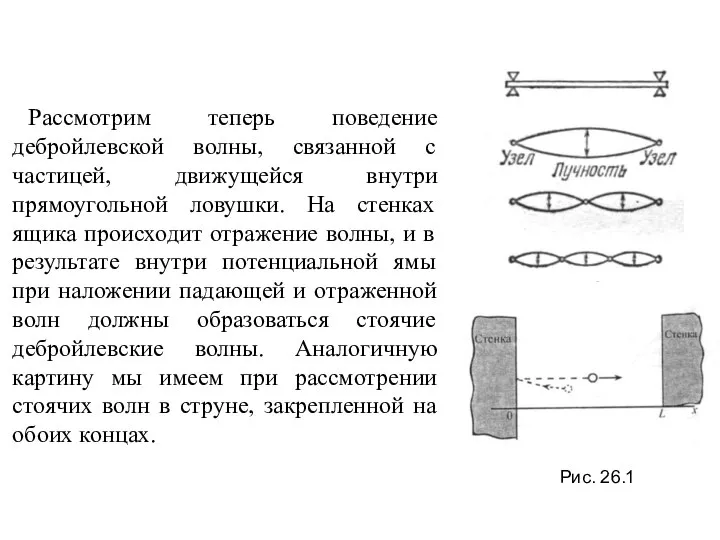
- 7. Рассмотрим теперь поведение дебройлевской волны, связанной с частицей, движущейся внутри прямоугольной ловушки. На стенках ящика происходит
- 8. Пусть длина струны равна L, а скорость волны в нем υ. При возбуждении колебаний в струне
- 9. Таким образом, длина стоячей волны не может быть произвольной. Она зависит от целых чисел n, поэтому
- 10. Формула (26.16) показывает, что частица, запертая внутри потенциальной ловушки прямоугольной формы, может иметь квантованные значения энергии,
- 11. Иногда говорят, что он находится в определенном стационарном квантовом состоянии n. Этим подчеркивается, что состояние электрона
- 12. (26.16’) Подставим в формулу (26.16') численные значения h = 6,62·10-34 Дж·с и m = 9,l·10-31 кг
- 13. Энергетические уровни расположены в этом случае столь тесно, что можно считать эти уровни практически непрерывными. Они
- 14. Теперь мы видим, что в случае ловушки макроскопических размеров энергия электрона также ведет себя классическим образом:
- 15. Рассмотрим, как зависит квантование энергии от величины квантового числа п. Для этого воспользуемся формулой (26.16') для
- 16. При больших квантовых числах выводы и результаты квантовой механики должны соответствовать классическим результатам, т. е. квантовые
- 17. В более общей формулировке принцип соответствия утверждает, что между любой физической теорией, которая является обобщением и
- 19. Скачать презентацию
Вначале рассмотрим случай, когда частица с массой т движется с постоянной
Вначале рассмотрим случай, когда частица с массой т движется с постоянной
s = A cos (ωt - kx), где A — амплитуда волны.
В квантовой механике показывается, что общим уравнением плоской дебройлевской волны является выражение
= А(cosα – isinα), (26.11)
где α = ωt - kx = (26.12)
Здесь E и p — энергия и импульс частицы, i —
Здесь E и p — энергия и импульс частицы, i —
Вероятность обнаружить частицу в объеме ΔV определяется по формуле |ψ|2 = ψψ* есть квадрат модуля ψ-функции, т. е. произведение ψ на ψ*-функцию, комплексно-сопряженную с ψ (иными словами, отличающуюся от ψ знаком при мнимой единице). Вычисляя произведение ψψ* , получим
| ψ |2 = ψψ* = A (cos α + i sin α) · A (cosα - i sin α) =
= A2 (cos2 α - i cos α sin α + i sin α cos α + sin2 α) = A2.
Итак, имеется постоянная, не зависящая от времени интенсивность волны де Бройля. В соответствии с физическим смыслом волн де Бройля это показывает, что имеется постоянная, одинаковая вероятность обнаружить частицу в любой точке на оси х.
С точки зрения соотношений неопределенностей свободное движение частицы с точно заданным импульсом р означает, что положение частицы
на оси х становится совершенно неопределенным. Об этом же говорит одинаковая
на оси х становится совершенно неопределенным. Об этом же говорит одинаковая
Выразим энергию частицы через длину волны де Бройля λ. По формуле λ = h/mυ, откуда υ = h/mλ. Подставив это в выражение энергии, получим
(26.13)
Наконец, учитывая, что λ = 2π/k, можно выразить энергию E через волновое число k:
На рис. 26.1 изображена парабола, выражающая зависимость энергии E свободной частицы от волновых чисел k дебройлевских волн частицы, т. е. от скорости υ = k/m.
(26.14)
k
E
Рис. 26.1
Рассмотрим теперь микроскопическую частицу, движение которой вдоль оси х ограничено следующим
Рассмотрим теперь микроскопическую частицу, движение которой вдоль оси х ограничено следующим
Частица в потенциальной яме прямоугольной формы
Рис. 26.1
Разумеется, таких ям практически не существует. Однако при изучении электропроводности металлов
Разумеется, таких ям практически не существует. Однако при изучении электропроводности металлов
В этой задаче мы встречаемся с ограничением движения
частицы. Она находится внутри прямоугольной ловушки — за-
перта в ней.
Форма ловушки зависит от потенциальной энергии частицы.
В данном случае потенциальная энергия частицы весьма просто зависит от координаты х: если x < 0 или x > L, то U = ∞; если 0 ≤ x ≤ L, то U = 0.
Рассмотрим теперь поведение дебройлевской волны, связанной с частицей, движущейся внутри прямоугольной
Рассмотрим теперь поведение дебройлевской волны, связанной с частицей, движущейся внутри прямоугольной
Рис. 26.1
Пусть длина струны равна L, а скорость волны в нем υ.
Пусть длина струны равна L, а скорость волны в нем υ.
L = nλn/2 или λn = 2L/n (где n =1, 2, 3, ...).
Выразив длину волны через частоту колебаний и скорость распространения волны, получим значения собственных частот:
ω = nπυ/L, v = ω/2π = nυ/2L.
(26.15)
Таким образом, длина стоячей волны не может быть произвольной. Она зависит
Таким образом, длина стоячей волны не может быть произвольной. Она зависит
Очевидно, что эти рассуждения применимы и к дебройлевской волне частицы, движущейся внутри прямоугольной ловушки. На длине потенциальной ямы должно уложиться целое число полуволн де Бройля. Формулу (26.13) теперь запишем несколько иначе:
(26.13’)
Индекс n у скорости υ и энергии E показывает, что скорость и энергия частицы в потенциальной прямоугольной ловушке не могут иметь произвольных значений. Вместе с длиной волны λ скорость и энергия будут квантованными величинами, принимающими лишь определенные дискретные значения. Подставим в (26.13') значения λn из (26.15). Получим
Формула (26.16) показывает, что
частица, запертая внутри потенциальной ловушки прямоугольной формы,
Формула (26.16) показывает, что
частица, запертая внутри потенциальной ловушки прямоугольной формы,
(n =1,2,3,….)
(26.16)
До сих пор речь шла о любой микроскопической частице, обладающей волновыми свойствами и запертой внутри ловушки. Предположим теперь для определенности, что мы говорим об электроне, находящемся в потенциальной ловушке. Квантованные значения En называются уровнями энергии, а числа n, определяющие энергетические уровни электрона, называются квантовыми числами. Таким образом, электрон в потенциальной яме может находиться на определенном энергетическом уровне.
Иногда говорят, что он находится в определенном стационарном квантовом состоянии n.
Иногда говорят, что он находится в определенном стационарном квантовом состоянии n.
Очень важно, что электрон не может обладать энергией, не совпадающей с одним из энергетических уровней. Дозволенными являются только такие энергии электрона в потенциальном ящике прямоугольной формы, которые совпадают с энергетическими уровнями, определяемыми формулой (26.16).
Рассмотрим влияние линейных размеров ловушки на квантование энергии. Покажем, что квантование энергии становится существенным лишь в том случае, когда линейные размеры потенциального ящика соизмеримы с размерами атома L= 1 нм =
=10-9 м. Для этого вычислим разность ΔE энергий электрона, находящегося на двух соседних энергетических уровнях En+1 и En. По формуле (26.16) имеем
(26.16’)
Подставим в формулу (26.16') численные значения h = 6,62·10-34 Дж·с и
(26.16’)
Подставим в формулу (26.16') численные значения h = 6,62·10-34 Дж·с и
«Расстояние» между соседними энергетическими уровнями с ростом n возрастает пропорционально ряду нечетных чисел (2n +1).
Для ящика макроскопических размеров L = 10-2 м аналогично получим следующие результаты:
Энергетические уровни расположены в этом случае столь тесно, что можно считать
Энергетические уровни расположены в этом случае столь тесно, что можно считать
При обсуждении роли соотношений неопределенностей для описания движений мы видели, что при макроскопическом движении частицы можно не принимать во внимание ограничений, которые вносят соотношения неопределенностей в возможность описывать движение с помощью понятия о траектории. Наоборот, при движении электрона в атоме, где он заперт в ловушке с линейными размерами порядка размеров атома, понятие о траектории частицы становится неправомерным.
Теперь мы видим, что в случае ловушки макроскопических размеров энергия электрона
Теперь мы видим, что в случае ловушки макроскопических размеров энергия электрона
Рассмотрим, как зависит квантование энергии от величины квантового числа п. Для
Рассмотрим, как зависит квантование энергии от величины квантового числа п. Для
При больших значениях квантового числа п имеем 2п+1\≈2п и отношение (26.17) дает
(26.17)
(26.18)
При больших квантовых числах выводы и результаты квантовой механики должны соответствовать
При больших квантовых числах выводы и результаты квантовой механики должны соответствовать
Принцип соответствия Бора
Видно, что при n >> 1 отношение ΔE/En << 1, или ΔE << En. Это означает, что при росте квантового числа n разность ближайших энергетических уровней растет медленнее, чем величина энергии каждого из уровней. Другими словами, с ростом n должно происходить относительное сближение энергетических уровней. При больших квантовых числах квантование энергии дает результаты, близкие к тем, которые получаются при классическом рассмотрении,— уровни становятся квазинепрерывными. В этом находит свое выражение принцип соответствия, в окончательном виде сформулированный Н. Бором в 1923 г.:
В более общей формулировке принцип соответствия утверждает, что между любой физической
В более общей формулировке принцип соответствия утверждает, что между любой физической















 Министерство образования и науки Российской Федерациии
Министерство образования и науки Российской Федерациии Берегите воду - презентация для начальной школы_
Берегите воду - презентация для начальной школы_ Личная гигиена. Гигиена кожи, одежды. Цель: объяснить значение личной гигиены для общего состояния здоровья; сформировать предста
Личная гигиена. Гигиена кожи, одежды. Цель: объяснить значение личной гигиены для общего состояния здоровья; сформировать предста Организация и размещение населения в защитных сооружениях Работу выполнила Зыкова Анна
Организация и размещение населения в защитных сооружениях Работу выполнила Зыкова Анна Расчет основного оборудования электрической части ТЭЦ 2×110;110 МВт
Расчет основного оборудования электрической части ТЭЦ 2×110;110 МВт ВОЗМОЖНОСТИ ИСПОЛЬЗОВАНИЯ ИКТ НА УРОКАХ ФИЗИЧЕСКОЙ КУЛЬТУРЫ Подготовила: Учитель физической культуры 1 квалификационной катег
ВОЗМОЖНОСТИ ИСПОЛЬЗОВАНИЯ ИКТ НА УРОКАХ ФИЗИЧЕСКОЙ КУЛЬТУРЫ Подготовила: Учитель физической культуры 1 квалификационной катег Основы проектной деятельности
Основы проектной деятельности 8429 и 8430 ТНВЭД ТС Терешкова М. ДС5 ФТД5
8429 и 8430 ТНВЭД ТС Терешкова М. ДС5 ФТД5 Ассортимент декоративных растений
Ассортимент декоративных растений Культура. Культурный комплекс. Культурное наследие. Культурные универсалии. Культурные нормы
Культура. Культурный комплекс. Культурное наследие. Культурные универсалии. Культурные нормы Thanksgiving Day
Thanksgiving Day Современные средства радиоконтроля производства предприятия ООО «Радиософт»
Современные средства радиоконтроля производства предприятия ООО «Радиософт» ЗДОРОВЬЕ и ВРЕДНЫЕ ПРИВЫЧКИ
ЗДОРОВЬЕ и ВРЕДНЫЕ ПРИВЫЧКИ Формы реализации права
Формы реализации права Малыш и Карлсон - часть 2 - презентация для начальной школы
Малыш и Карлсон - часть 2 - презентация для начальной школы Повторение курса «Христианские добродетели»
Повторение курса «Христианские добродетели» Духовная жизнь серебряного века
Духовная жизнь серебряного века Особенности восприятия изобразительного искусства Выполнила: Накраплённая Е.А.
Особенности восприятия изобразительного искусства Выполнила: Накраплённая Е.А. Производственно-техническая база предприятий автосервиса (Лекция № 5)
Производственно-техническая база предприятий автосервиса (Лекция № 5) Витамины и минеральный обмен
Витамины и минеральный обмен Абсолютные относительные и средние величины
Абсолютные относительные и средние величины Современные подходы к управлению производственными предприятиями
Современные подходы к управлению производственными предприятиями Введение в язык шейдеров OpenGL
Введение в язык шейдеров OpenGL Порядок надання адміністративних послуг, насамперед базових, і параметри якості послуг
Порядок надання адміністративних послуг, насамперед базових, і параметри якості послуг Презентация Роль и значение таможни в современной торговле
Презентация Роль и значение таможни в современной торговле 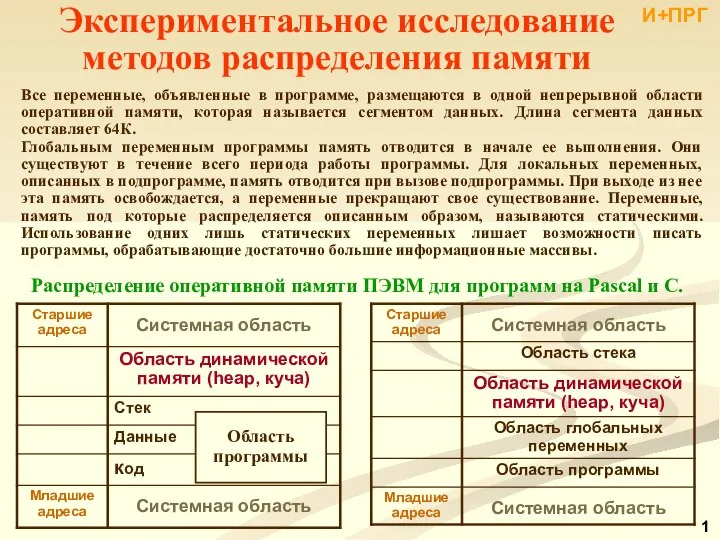 Распределение памяти
Распределение памяти Причины снижения продуктивности скважин при РНМ
Причины снижения продуктивности скважин при РНМ Строки в Pascal. Решение задач
Строки в Pascal. Решение задач