Содержание
- 2. Метод возник и разработан в эпоху великих географических открытий. Гауссу (Carl Friedrich Gauss) приписывают создание основ
- 3. Наиболее ранний анализ систем линейных алгебраических уравнений приводится в древней китайской книге «Девять глав арифметики», предположительно
- 4. Метод решения задачи, предложенный древними китайцами, заключался в следующем. Разноцветные бамбуковые палочки, представляющие коэффициенты системы уравнений,
- 5. 16.10.2012 1820 watercolor charicatures of the French mathematicians Adrien-Marie Legendre (left) and Joseph Fourier (right) by
- 6. Карл Фридрих Гаусс 16.10.2012 Carl Friedrich Gauss (1777–1855), painted by Christian Albrecht Jensen
- 7. Цель состоит в подборе параметров пробной функции, описывающей экспериментальный набор данных. Простой набор данных состоит из
- 8. Одним из важных приложений нелинейного метода наименьших квадратов является задача подбора коэффициентов нелинейной модели. При этом
- 9. Обычная формулировка проблемы наименьших квадратов: Выбираем функцию, описывающую моделируемое явление: и хотим подобрать параметры модели таким
- 10. Минимизировать отыскав оптимальные значения параметров Здесь весовые коэффициенты задаются диагональной матрицей Метод наименьших квадратов 16.10.2012
- 11. Найти оптимальные значения параметров и , минимизировав Весовые коэффициенты задаются диагональными матрицами Обобщенный метод наименьших квадратов
- 12. Обобщенная проблема может быть решена с помощью любого метода минимизации нелинейной функции по (n+m) переменным не
- 13. где Решение по методу Ньютона 16.10.2012
- 14. Матрица является диагональной с элементами Метод Ньютона решения этой задачи приводит к решению системы линейных уравнений
- 15. При разработке методов решения полной задачи о наименьших квадратах важно учитывать специфическую структуру целевой функции и
- 16. Задача оптимизации называется сепарабельной, если ее оптимизация по одним переменным много проще, чем по другим. Обобщенная
- 17. В этом случае внедиагональные элементы матрицы обращаются в ноль и обе матрицы и становятся диагональными. Предполагая,
- 18. Полиномы ,ортогональные на множестве , могут быть получены по рекуррентным формулам где Приближенные методы Ньютона 16.10.2012
- 19. Итерации приближенного метода Ньютона начинаются с начальной точки и . Затем на каждой итерации вначале вычисляются
- 21. Скачать презентацию

















 Антифрикационные материалы
Антифрикационные материалы Конструкций конструкций
Конструкций конструкций Подсистемы системы «Корабль». Подсистема "Маневрирование"
Подсистемы системы «Корабль». Подсистема "Маневрирование" Свет и освещение
Свет и освещение Контроль знаний
Контроль знаний CRM On Demand Владимир Карагиоз
CRM On Demand Владимир Карагиоз  Präsentation_DSG Studiengänge_Russisch
Präsentation_DSG Studiengänge_Russisch Postawy liturgiczne
Postawy liturgiczne РЕГУЛЯЦИЯ РЕПРОДУКТИВНОЙ ФУНКЦИИ ЖЕНЩИНЫ
РЕГУЛЯЦИЯ РЕПРОДУКТИВНОЙ ФУНКЦИИ ЖЕНЩИНЫ Русская архитектура. Церкви и соборы
Русская архитектура. Церкви и соборы Динамика развития периферического рака лёгкого
Динамика развития периферического рака лёгкого  Практические аспекты интеллектуальной собственности
Практические аспекты интеллектуальной собственности Презентация Определяющие тенденции эволюции сферы внешнеэкономической и таможенной деятельности России
Презентация Определяющие тенденции эволюции сферы внешнеэкономической и таможенной деятельности России  Инженерная графика
Инженерная графика 7 чудес земли Амурской
7 чудес земли Амурской Стандартные строковые функции языка CLIPS
Стандартные строковые функции языка CLIPS Молодежный сленг и жаргон
Молодежный сленг и жаргон Расчет цен
Расчет цен  Теория, политическая элита
Теория, политическая элита Урок 2. площадь треугольника
Урок 2. площадь треугольника Лесные ресурсы мира
Лесные ресурсы мира Шаблон презентации на Demo Day
Шаблон презентации на Demo Day Определение численности персонала предприятия
Определение численности персонала предприятия Понятия «схемотехника», «телекоммуникационные устройства»
Понятия «схемотехника», «телекоммуникационные устройства» Презентация "Гойя, Франсиско" - скачать презентации по МХК
Презентация "Гойя, Франсиско" - скачать презентации по МХК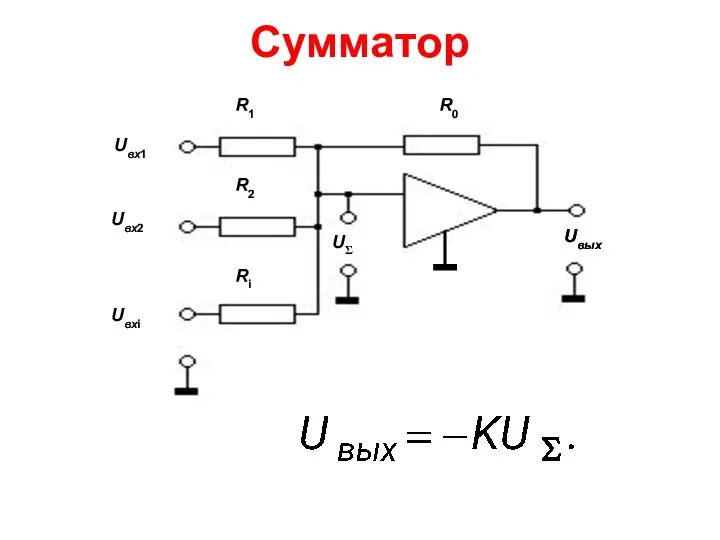 Аналогсумматор
Аналогсумматор Государственный Дарвиновский музей
Государственный Дарвиновский музей Народные промыслы России
Народные промыслы России