Содержание
- 2. Линейный поиск Методика линейного поиска Рассмотрим итеративные методы, останавливающиеся при выполнении некоторого критерия останова итеративного процесса.
- 3. Однако простейшая процедура, заключающаяся в выборе достаточно большого начального значения , которое затем уменьшается (делением пополам)
- 4. Это требование обеспечивает некую усредненную скорость спуска на очередной итерации не меньше определенной доли от величины,
- 5. Свойство. Предположим, что для всех . Тогда существует интервал такой, что в методе спуска условия (*)
- 6. Линейный поиск
- 7. http://www.hbmeyer.de/backtrack/backtren.htm Поиск с возвратом (англ. Backtracking) — общий метод нахождения решений задачи, в которой требуется полный
- 8. Методы оптимизации Методы спуска минимизации квадратичных функций Для методов спуска особый интерес представляют такие функции, для
- 9. Методы спуска для квадратичных функций В частности, при заданном направлении спуска можно определить оптимальную величину шага
- 10. Методы спуска для квадратичных функций Отклонение от точного решения на -м шаге процесса минимизации можно вычислить
- 11. Методы спуска для квадратичных функций С другой стороны, поэтому из предыдущей формулы следует, что Обозначим ,
- 12. Метод наискорейшего спуска Поскольку матрица A симметрична и положительно определена, то всегда положительна. Более того, можно
- 13. Лемма. (Неравенство Канторовича) Пусть - симметричная положительно определенная матрица с наибольшим и наименьшим по модулю значениями
- 14. Соответствующие методы обладают следующим хорошим свойством: Свойство. Метод вычисления точки минимума квадратичной функции, основанный на вычислении
- 15. Метод сопряженных направлений A-сопряженные направления можно вычислять в соответствии со следующей процедурой. Для начального приближения положим
- 16. Скорость сходимости метода может быть повышена лишь за счет проведения предобуславливания матрицы с целью уменьшения числа
- 17. Метод сопряженных направлений Иллюстрация последовательных приближений метода наискорейшего спуска (зелёная ломаная) и метода сопряжённых градиентов (красная
- 18. Метод сопряженных градиентов The algorithm is detailed for solving Ax = b where A is a
- 19. The gradient method
- 20. The gradient method
- 21. The gradient method Alfio Quarteroni, Riccardo Sacco, Fausto Saleri Numerical Mathematics
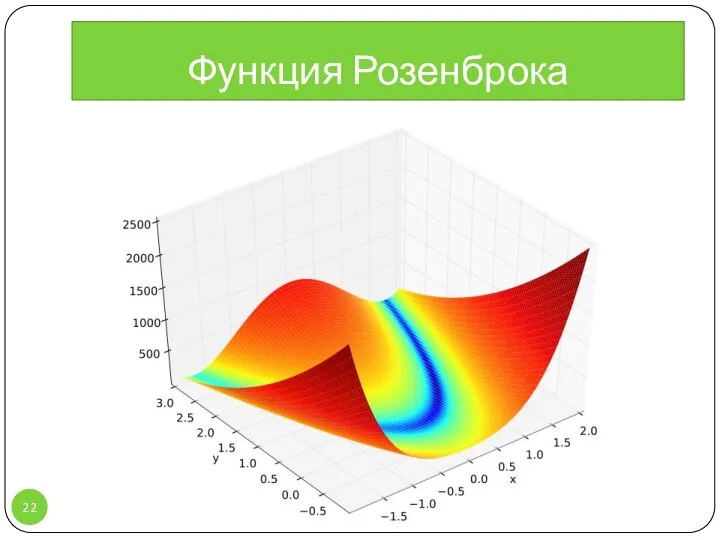
- 22. Функция Розенброка
- 24. Скачать презентацию




















 Виды соединений составных частей изделия
Виды соединений составных частей изделия Визитная карточка Сеула, Южная Корея
Визитная карточка Сеула, Южная Корея Контроль качества при производстве тыквенных цукат
Контроль качества при производстве тыквенных цукат Политические пиар - технологии
Политические пиар - технологии Продажа коммерческих помещений в ЖК «Палацио»
Продажа коммерческих помещений в ЖК «Палацио» ФИНАНСОВЫЙ КРИЗИС: причины возникновения и пути выхода Берзон Н.И. Д.э.н., профессор,
ФИНАНСОВЫЙ КРИЗИС: причины возникновения и пути выхода Берзон Н.И. Д.э.н., профессор,  Презентация на тему "Видеообучение - одна из форм дистанционного обучения" - скачать презентации по Педагогике
Презентация на тему "Видеообучение - одна из форм дистанционного обучения" - скачать презентации по Педагогике Цель и основные задачи инженерного обеспечения современного общевойскового боя. Общая тактика
Цель и основные задачи инженерного обеспечения современного общевойскового боя. Общая тактика Расщепитель фаз НБ-455
Расщепитель фаз НБ-455 Cosmology
Cosmology Презентация на тему "Работа с родителями как одно из направлений деятельности классного руководителя" - скачать презентации
Презентация на тему "Работа с родителями как одно из направлений деятельности классного руководителя" - скачать презентации  Презентация КЛАССИКИ ПОЛИТИЧЕСКОЙ ЭКОНОМИИ ОБ УПРАВЛЕНИИ (XVIII-XIXBB.)
Презентация КЛАССИКИ ПОЛИТИЧЕСКОЙ ЭКОНОМИИ ОБ УПРАВЛЕНИИ (XVIII-XIXBB.) Система каротажа при бурении. Занятие 9
Система каротажа при бурении. Занятие 9 Презентация 1 Big Data
Презентация 1 Big Data Моторное масло
Моторное масло Системы связи. Телекоммуникационные сети
Системы связи. Телекоммуникационные сети Значение фамилий. Этимология
Значение фамилий. Этимология Урок чтения 4 класс
Урок чтения 4 класс Возникновение и развитие египтологии
Возникновение и развитие египтологии  Разработка информационно-измерительной системы контроля и учёта энергоресурсов на базе сумматора «СЭМ-2.01» завода
Разработка информационно-измерительной системы контроля и учёта энергоресурсов на базе сумматора «СЭМ-2.01» завода доступная среда, универсальный дизайн
доступная среда, универсальный дизайн  Ферменты
Ферменты Открытые спортивно-массовые соревнования «Дог-квест «Хвостатая тропа». Соревнования по спортивному ориентированию на велосипеда
Открытые спортивно-массовые соревнования «Дог-квест «Хвостатая тропа». Соревнования по спортивному ориентированию на велосипеда Специальное снаряжение
Специальное снаряжение Программирование циклических алгоритмов. Начала программирования
Программирование циклических алгоритмов. Начала программирования Биография Дарвина
Биография Дарвина Энзимопатии
Энзимопатии  франц
франц