Содержание
- 2. Методы интегрирования 4) Замена переменной Часть подынтегральной функции или вся функция Ψ(х) заменяется новой переменной, т.е.:
- 3. Пример: Найти Сделаем замену 3х=t Теперь…
- 4. 2) Замена Теперь Или и тогда и т.д.
- 5. 3) Пример Делаем замену Подставляем через t в подынтегральное выражение:
- 6. 5) Метод преобразования дифференциала Справедливы следующие формулы:
- 7. Примеры 1) 2) 3)
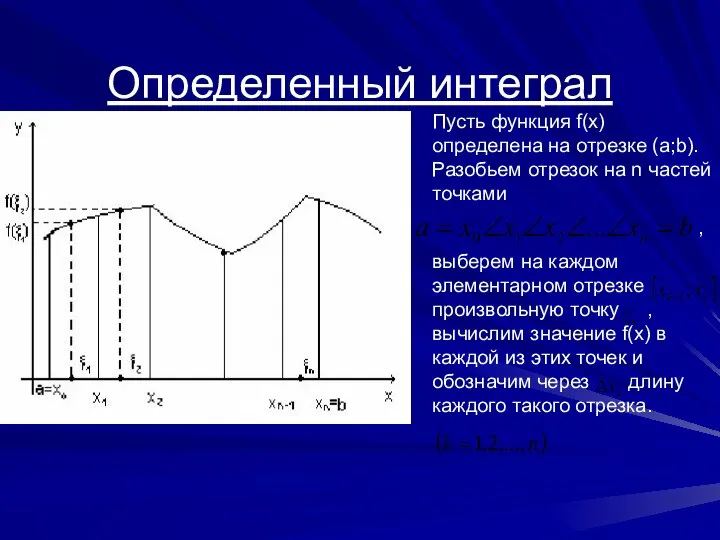
- 8. Определенный интеграл Пусть функция f(x) определена на отрезке (a;b). Разобьем отрезок на n частей точками ,
- 9. Определение 1: Сумма вида называется интегральной суммой для f(x) на отрезке Определение 2: Устремим максимальную длину
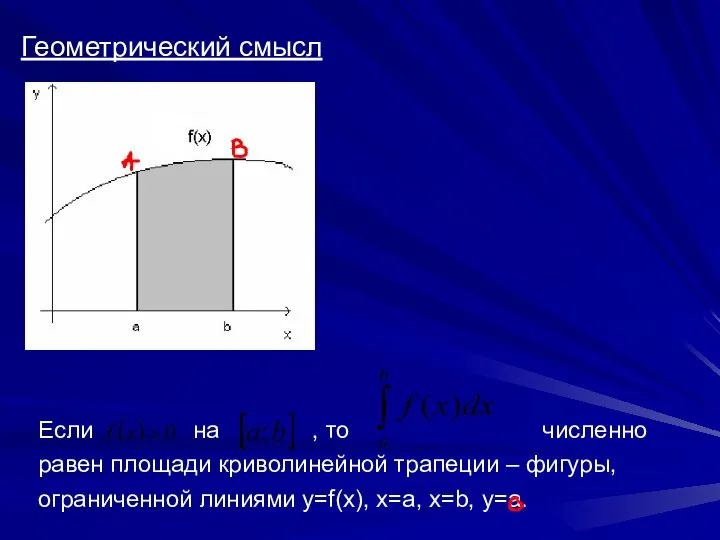
- 10. Геометрический смысл Если на , то численно равен площади криволинейной трапеции – фигуры, ограниченной линиями y=f(x),
- 11. Основные свойства определенного интеграла Если , то - формула Ньютона-Лейбница Здесь F(x) – первообразная для f(x).
- 12. 3) Т.е. при перестановке пределов интегрирования меняется знак интеграла. 4) Определенный интеграл с одинаковыми пределами интегрирования
- 13. 5) Т.е. отрезок интегрирования можно разбивать на части. 6)
- 14. Примеры 1.Вычислить Найдем первообразную Возьмем Тогда получаем по формуле Ньютона-Лейбница
- 15. 2. Вычислить Найдем первообразную Выберем Тогда
- 17. Скачать презентацию












 Блок управления установкой охлаждения жидкости
Блок управления установкой охлаждения жидкости ОСНОВЫ ТЕОРИИ УПРАВЛЕНИЯ ОБРАЗОВАТЕЛЬНЫМИ СИСТЕМАМИ
ОСНОВЫ ТЕОРИИ УПРАВЛЕНИЯ ОБРАЗОВАТЕЛЬНЫМИ СИСТЕМАМИ  Мультимедийное оборудование. Проекторы, интерактивные доски
Мультимедийное оборудование. Проекторы, интерактивные доски Map of the city with regional points of attraction
Map of the city with regional points of attraction Образ художественной культуры Средней Азии
Образ художественной культуры Средней Азии Вторая модель Эрланга. (Лекция 8)
Вторая модель Эрланга. (Лекция 8) Введення. Третя пречиста
Введення. Третя пречиста Логарифмические уравнения - презентация по Алгебре
Логарифмические уравнения - презентация по Алгебре Работа с дисками
Работа с дисками Умножение обыкновенной дроби на натуральное число - презентация по Алгебре
Умножение обыкновенной дроби на натуральное число - презентация по Алгебре Исследование торговых комплексов Москвы
Исследование торговых комплексов Москвы Сердечно-сосудистые риски Основы безопасного поведения (по мотивам записей в амбулаторных картах)
Сердечно-сосудистые риски Основы безопасного поведения (по мотивам записей в амбулаторных картах) Методические рекомендации для проведения анализа современного урока
Методические рекомендации для проведения анализа современного урока АППАРАТУРА АВТОМАТИЧЕСКОГО ИЗМЕРЕНИЯ ПЕЛЕНГА СТАНЦИИ ПОМЕХ КВ РАДИОСВЯЗИ
АППАРАТУРА АВТОМАТИЧЕСКОГО ИЗМЕРЕНИЯ ПЕЛЕНГА СТАНЦИИ ПОМЕХ КВ РАДИОСВЯЗИ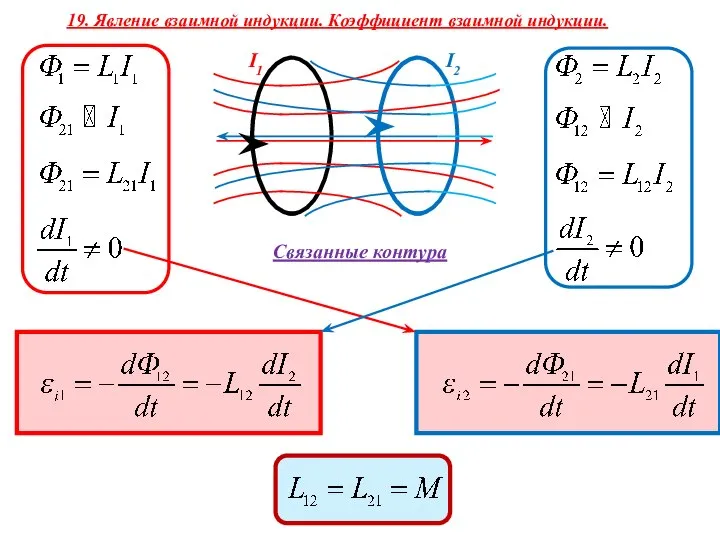 Взаимная индукция. Энергия магн.поля
Взаимная индукция. Энергия магн.поля Service вulletin. SVC мodel
Service вulletin. SVC мodel ЗАНЯТИЕ КРУЖКА ПО РАЗВИТИЮ ТВОРЧЕСКИХ СПОСОБНОСТЕЙ (НАЧАЛЬНАЯ ГЕОМЕТРИЯ) 1 КЛАСС
ЗАНЯТИЕ КРУЖКА ПО РАЗВИТИЮ ТВОРЧЕСКИХ СПОСОБНОСТЕЙ (НАЧАЛЬНАЯ ГЕОМЕТРИЯ) 1 КЛАСС VIII Aula de português
VIII Aula de português Аттестационная работа. Тайна исторической народной песни
Аттестационная работа. Тайна исторической народной песни Юпитер
Юпитер Функциональные схемы систем автоматизации технологических процессов
Функциональные схемы систем автоматизации технологических процессов Презентация Основные направления деятельности главных управлений Центрального аппарата ФТС России
Презентация Основные направления деятельности главных управлений Центрального аппарата ФТС России  Электронные регуляторы скорости Electronic speed controller (ESC)
Электронные регуляторы скорости Electronic speed controller (ESC) Цифровая логика
Цифровая логика Циклы. Компьютерные основы программирования. Представление программ, часть 3
Циклы. Компьютерные основы программирования. Представление программ, часть 3 Корпусные приспособления и вспомогательные элементы
Корпусные приспособления и вспомогательные элементы Нанесение размеров на чертежах Решение задач на тему «Построение изображений»
Нанесение размеров на чертежах Решение задач на тему «Построение изображений» Виды и формы бизнеса
Виды и формы бизнеса