Содержание
- 2. Начертательная геометрия является тем разделом геометрии, в котором изучаются методы изображения пространственных фигур на чертеже и
- 3. Чертежи должны не только определять форму и размеры предмета, но и быть достаточно простыми и точными
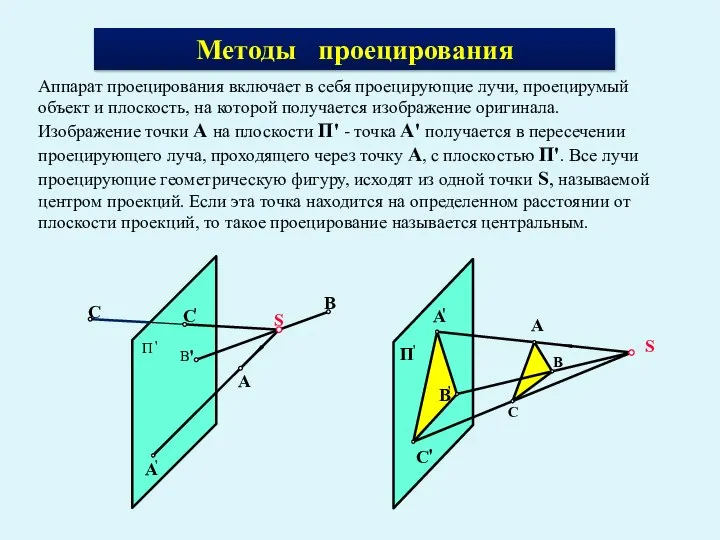
- 4. S A B C A S C B Методы проецирования Аппарат проецирования включает в себя проецирующие
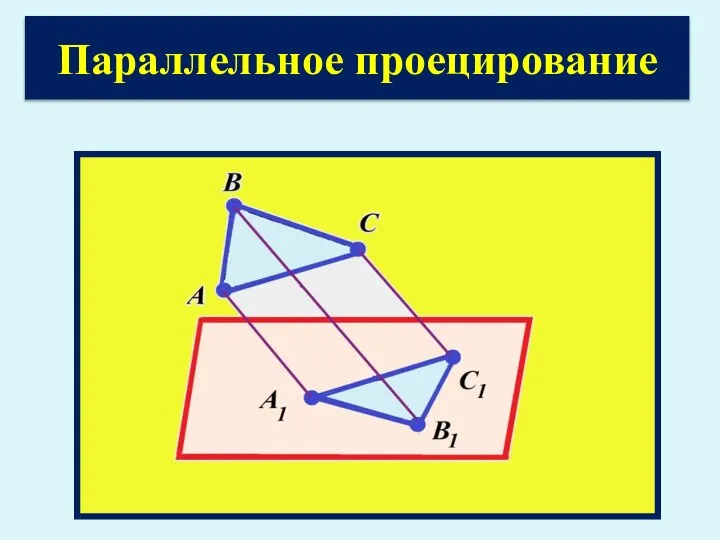
- 5. Параллельное проецирование
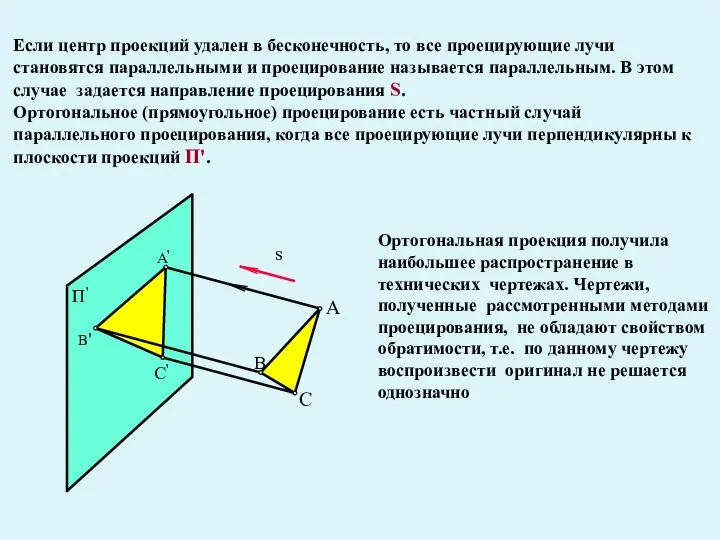
- 6. Если центр проекций удален в бесконечность, то все проецирующие лучи становятся параллельными и проецирование называется параллельным.
- 7. Основные свойства параллельного проецирования 1. Свойство однозначности. Проекцией точки на плоскость есть точка. 2. Свойство прямолинейности.
- 8. Точка - основной геометрический элемент линий, плоскостей, поверхностей и тел, следовательно, правила построения чертежа справедливы для
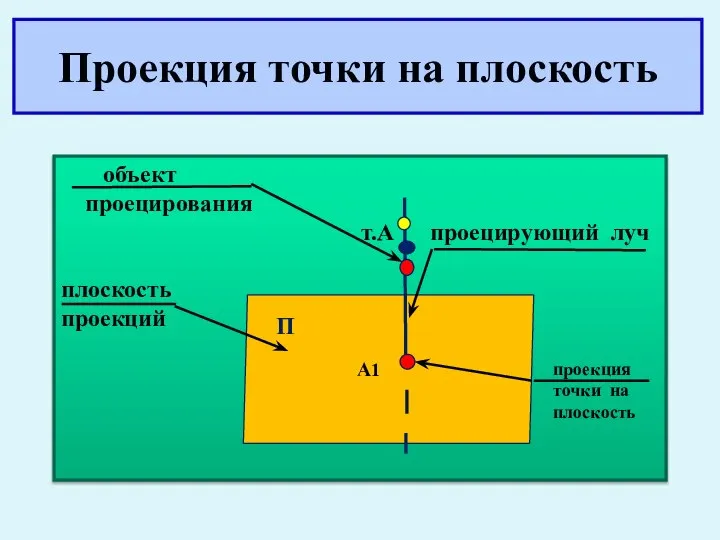
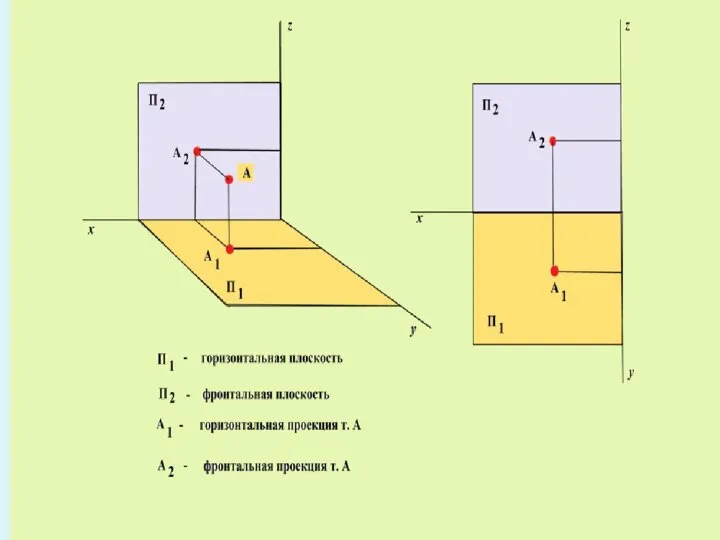
- 9. Проекция точки на плоскость объект проецирования т.А проецирующий луч плоскость проекций П А1 проекция точки на
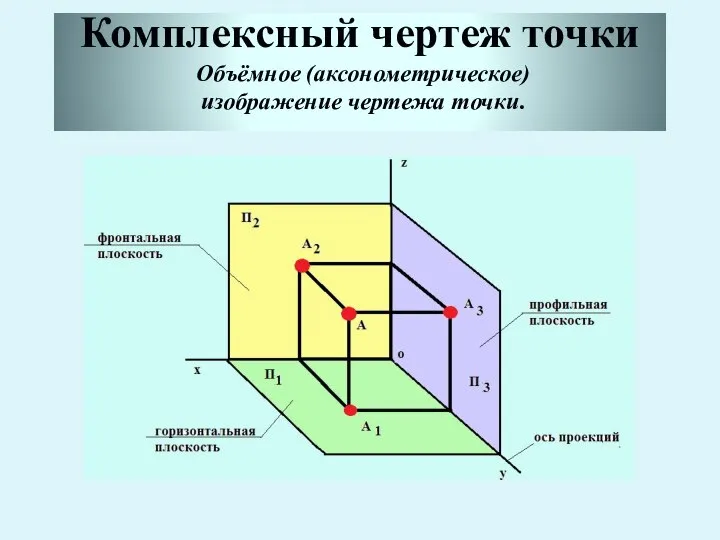
- 11. Комплексный чертеж точки Объёмное (аксонометрическое) изображение чертежа точки.
- 12. Комплексным чертежом точки – называется чертеж, состоящий из нескольких связанных между собой прямоугольных проекций точки.
- 13. Линии пересечения плоскостей проекций называются осями координат x, y, z. КОМПЛЕКСНЫЙ ЧЕРТЕЖ ТОЧКИ (ЭПЮР ТОЧКИ) Комплексный
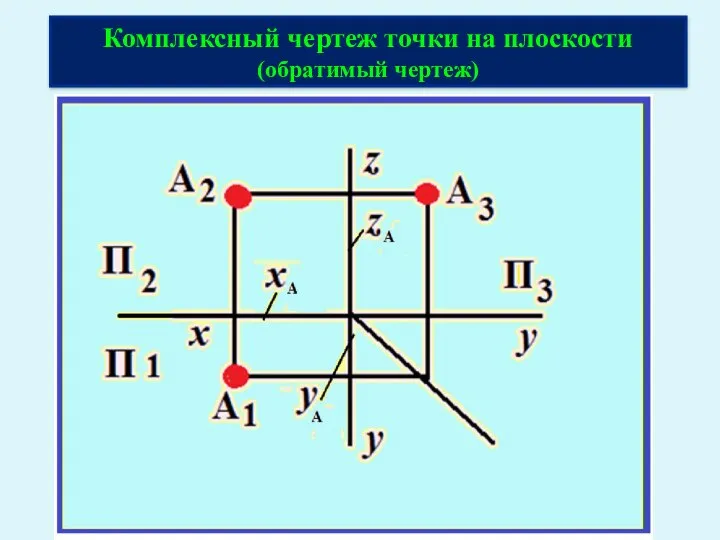
- 14. Комплексный чертеж точки на плоскости (обратимый чертеж)
- 15. Условия связи на комплексном чертеже : А2 и А3 – на одной горизонтальной линии связи; А2
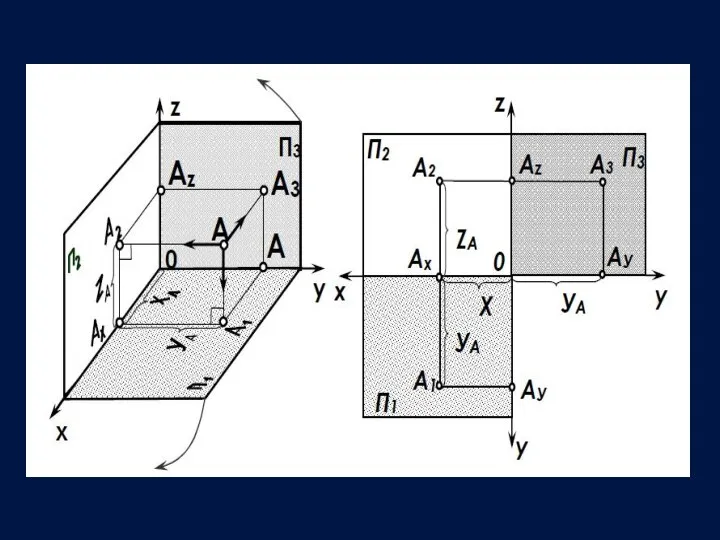
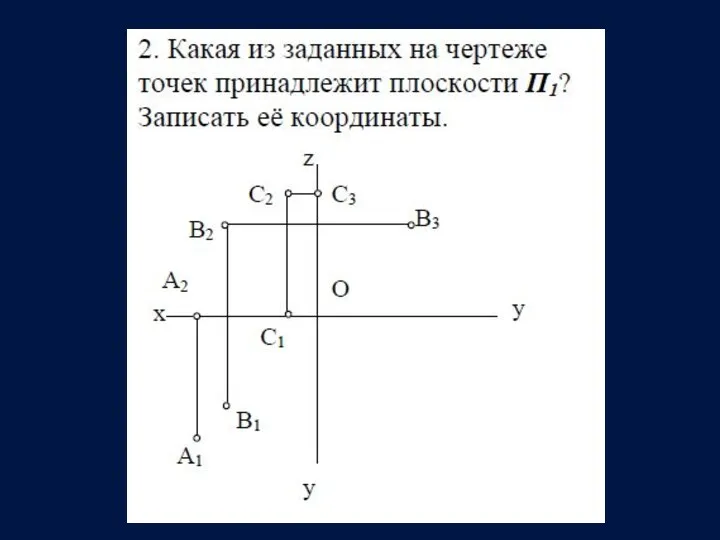
- 16. Определитель точки пространства – две её проекции, а также три прямоугольные координаты. Принимается, что плоскости проекций
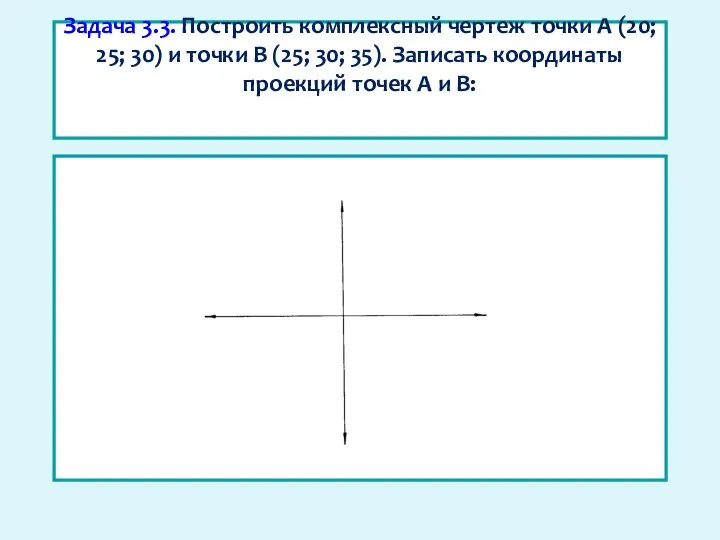
- 21. Задача 3.3. Построить комплексный чертеж точки А (20; 25; 30) и точки В (25; 30; 35).
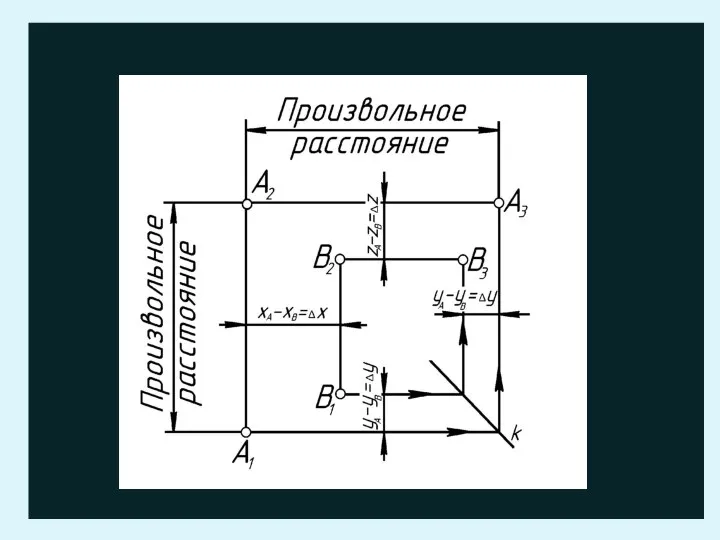
- 22. Безосный чертеж Изображение должно обеспечить наглядность, точность формы и размеров предмета, а не его расположение относительно
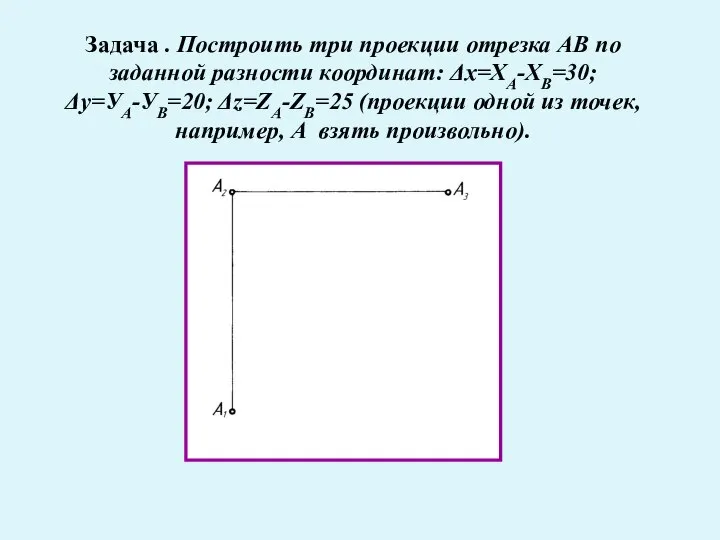
- 24. Задача . Построить три проекции отрезка АВ по заданной разности координат: Δх=ХА-ХВ=30; Δу=УА-УВ=20; Δz=ZA-ZB=25 (проекции одной
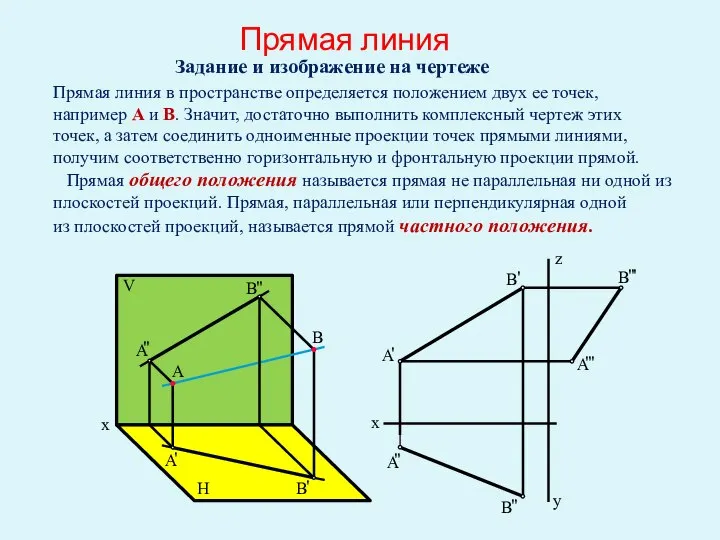
- 25. Прямая линия Задание и изображение на чертеже Прямая линия в пространстве определяется положением двух ее точек,
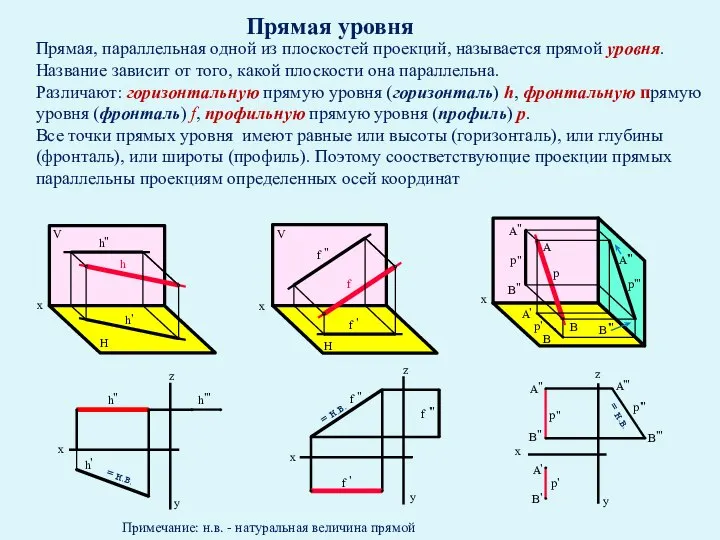
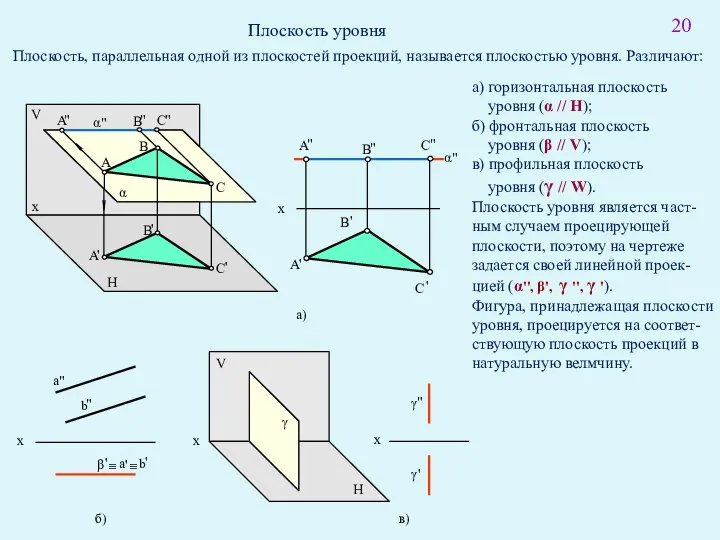
- 26. Прямая уровня Прямая, параллельная одной из плоскостей проекций, называется прямой уровня. Название зависит от того, какой
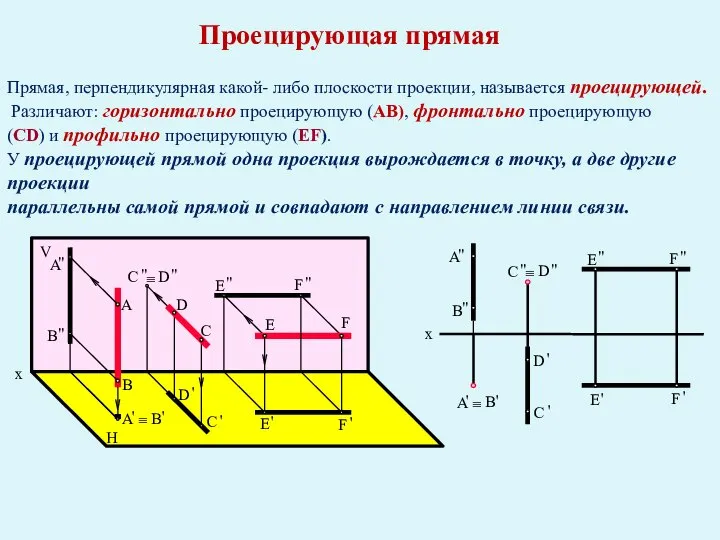
- 27. Проецирующая прямая Прямая, перпендикулярная какой- либо плоскости проекции, называется проецирующей. Различают: горизонтально проецирующую (AB), фронтально проецирующую
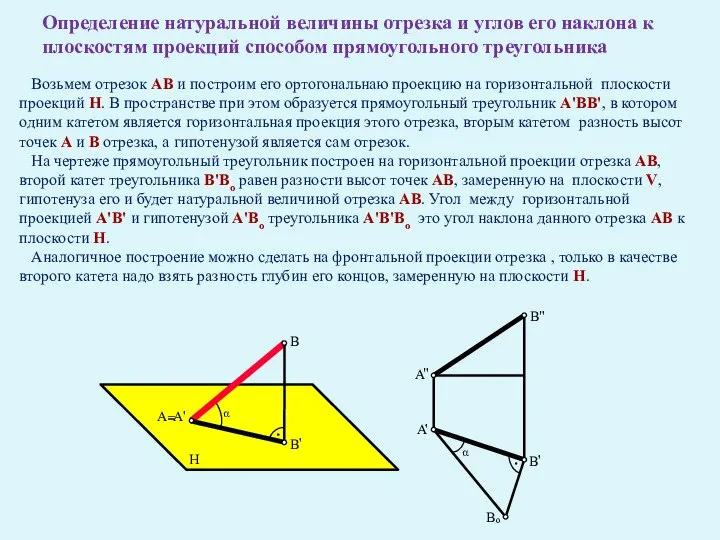
- 28. Определение натуральной величины отрезка и углов его наклона к плоскостям проекций способом прямоугольного треугольника Возьмем отрезок
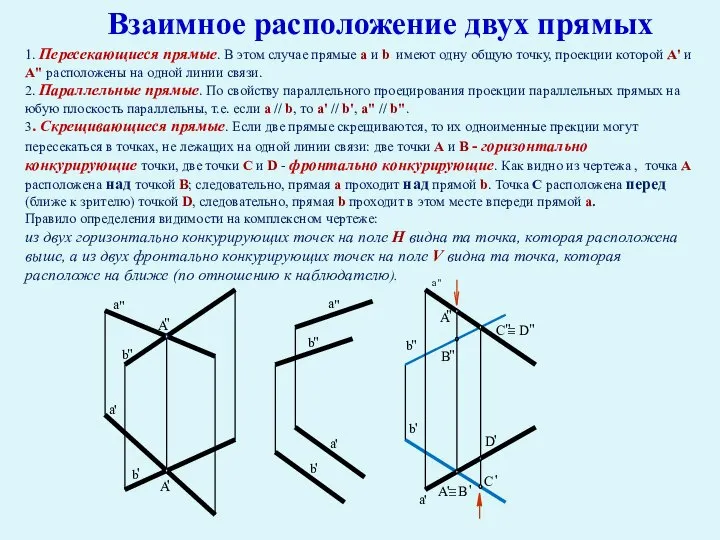
- 29. 1. Пересекающиеся прямые. В этом случае прямые a и b имеют одну общую точку, проекции которой
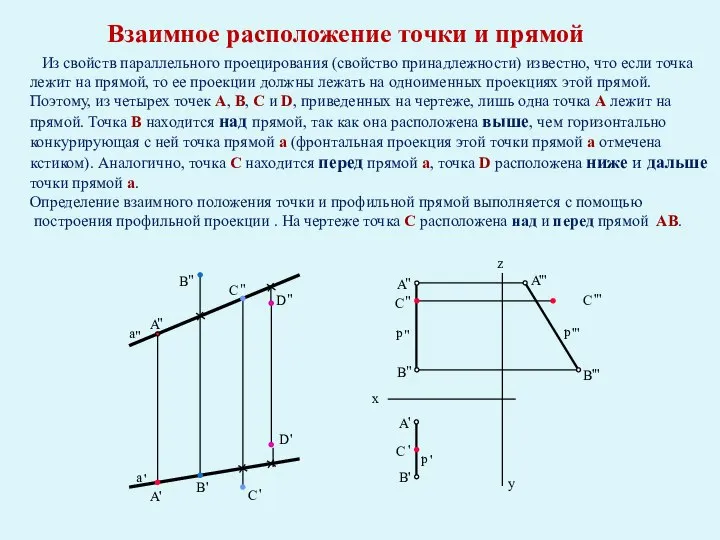
- 30. Из свойств параллельного проецирования (свойство принадлежности) известно, что если точка лежит на прямой, то ее проекции
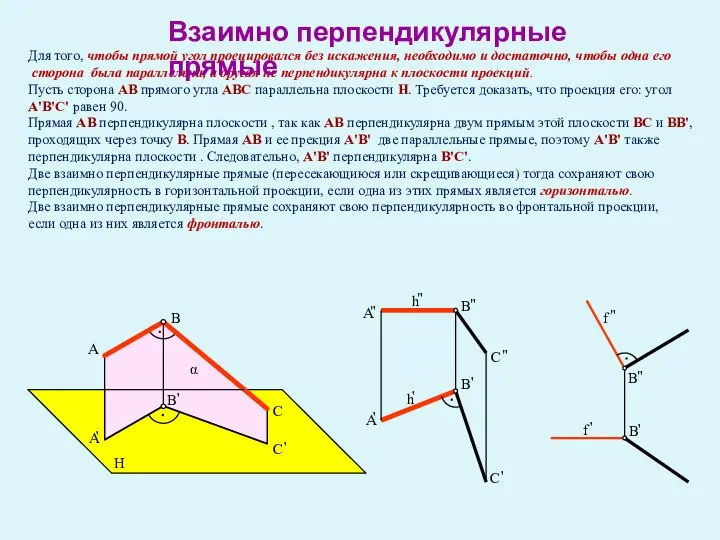
- 31. Для того, чтобы прямой угол проецировался без искажения, необходимо и достаточно, чтобы одна его сторона была
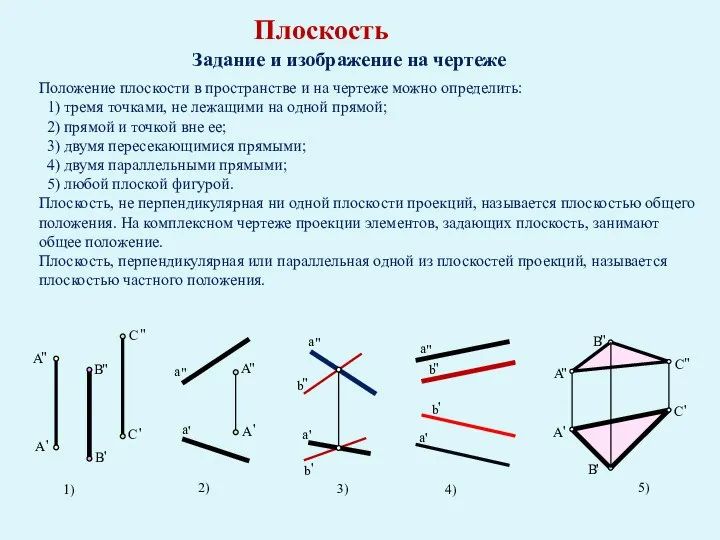
- 32. Плоскость Задание и изображение на чертеже Положение плоскости в пространстве и на чертеже можно определить: 1)
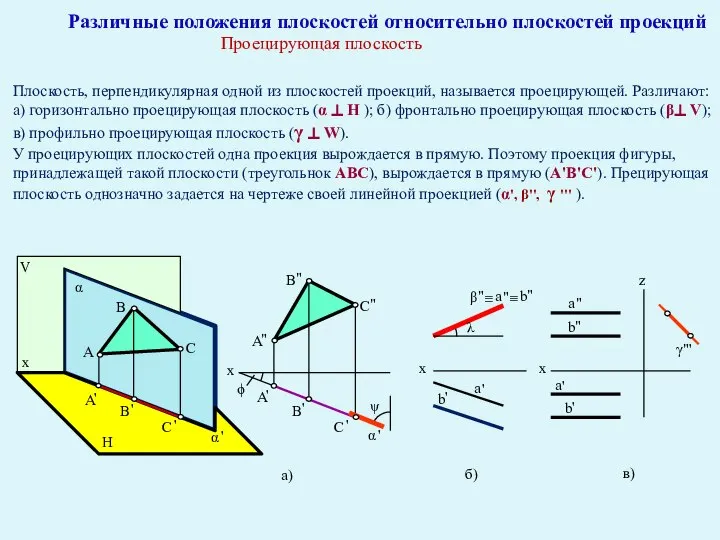
- 33. Различные положения плоскостей относительно плоскостей проекций Проецирующая плоскость Плоскость, перпендикулярная одной из плоскостей проекций, называется проецирующей.
- 34. A B C H V α x x x γ x V H x а) б)
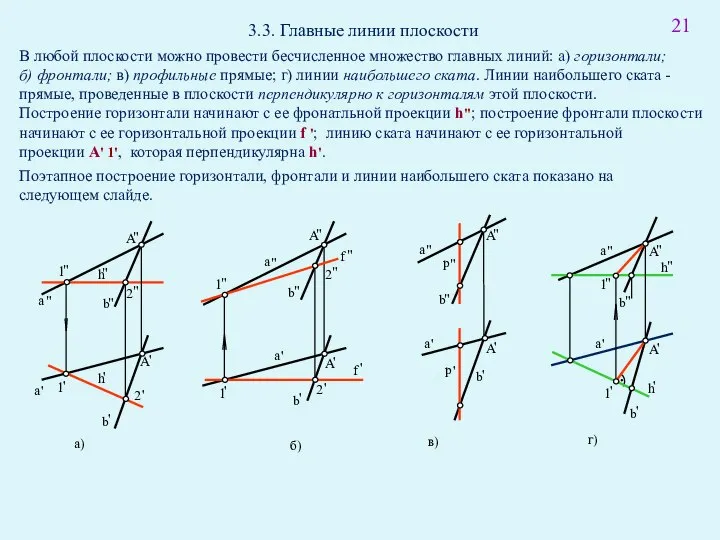
- 35. 3.3. Главные линии плоскости В любой плоскости можно провести бесчисленное множество главных линий: а) горизонтали; б)
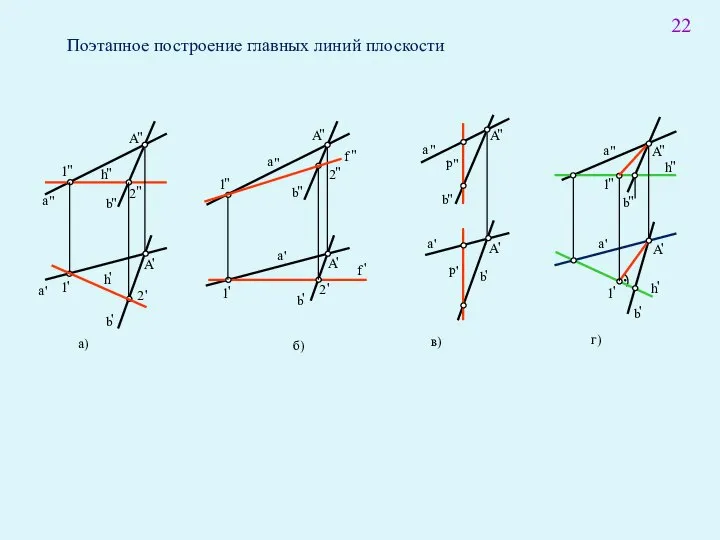
- 36. Поэтапное построение главных линий плоскости 2 ' а) б) в) г) 22
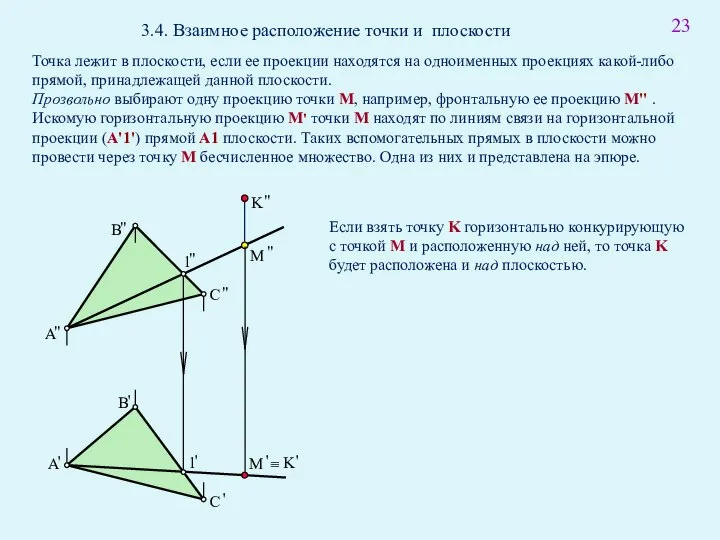
- 37. 3.4. Взаимное расположение точки и плоскости Точка лежит в плоскости, если ее проекции находятся на одноименных
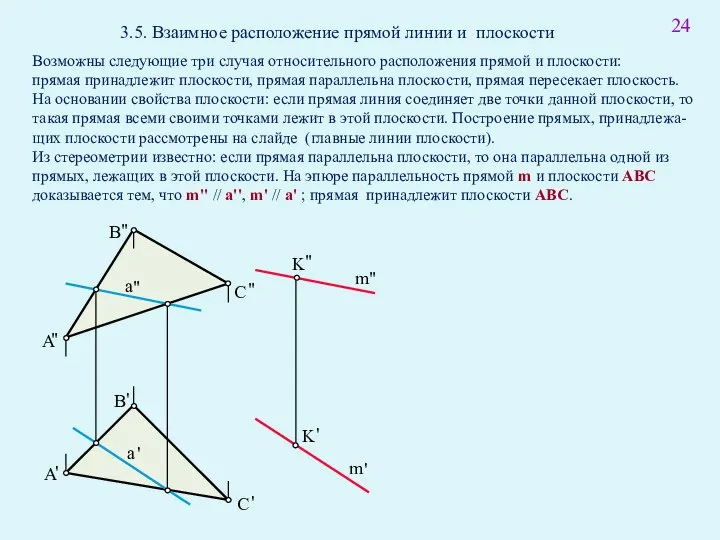
- 38. 3.5. Взаимное расположение прямой линии и плоскости Возможны следующие три случая относительного расположения прямой и плоскости:
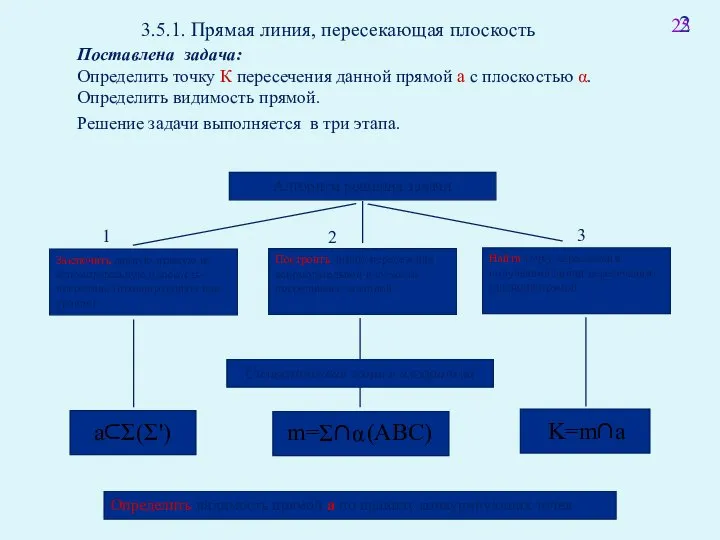
- 39. 3.5.1. Прямая линия, пересекающая плоскость Поставлена задача: Определить точку К пересечения данной прямой а с плоскостью
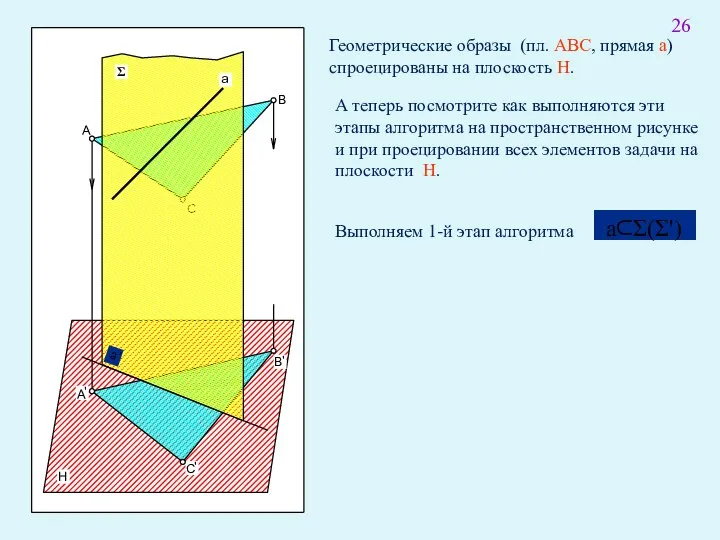
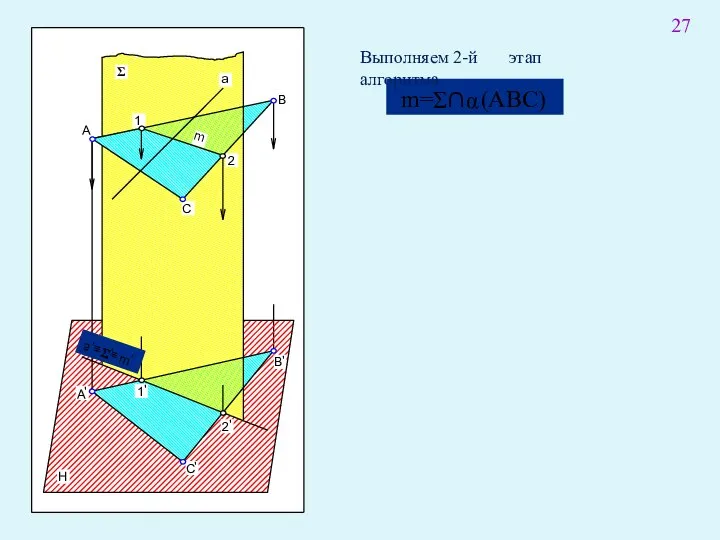
- 40. А теперь посмотрите как выполняются эти этапы алгоритма на пространственном рисунке и при проецировании всех элементов
- 41. Выполняем 2-й этап алгоритма 27
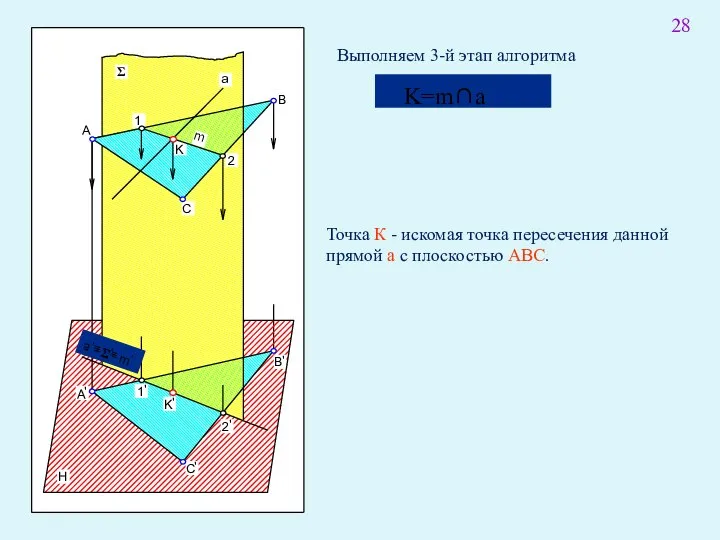
- 42. Точка К - искомая точка пересечения данной прямой а с плоскостью АВС. Выполняем 3-й этап алгоритма
- 43. Рассмотрим применение данного алгоритма при решении задачи на построение точки К пересечения прямой а с плоскостью
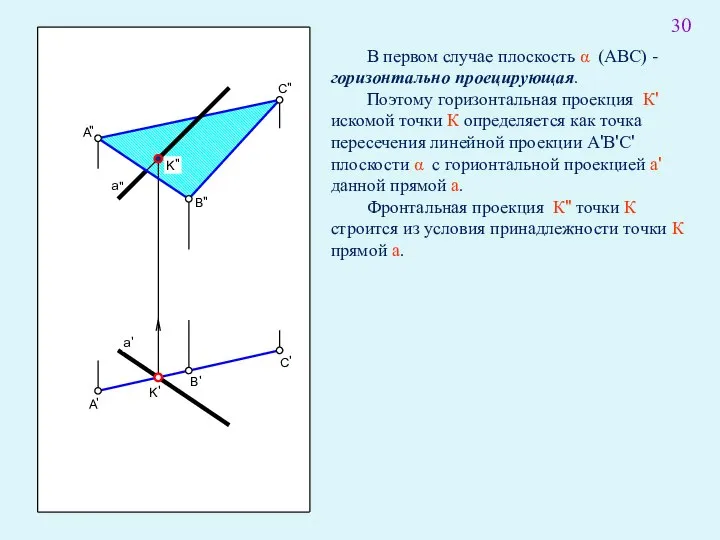
- 44. В первом случае плоскость α (АВС) - горизонтально проецирующая. Поэтому горизонтальная проекция К' искомой точки К
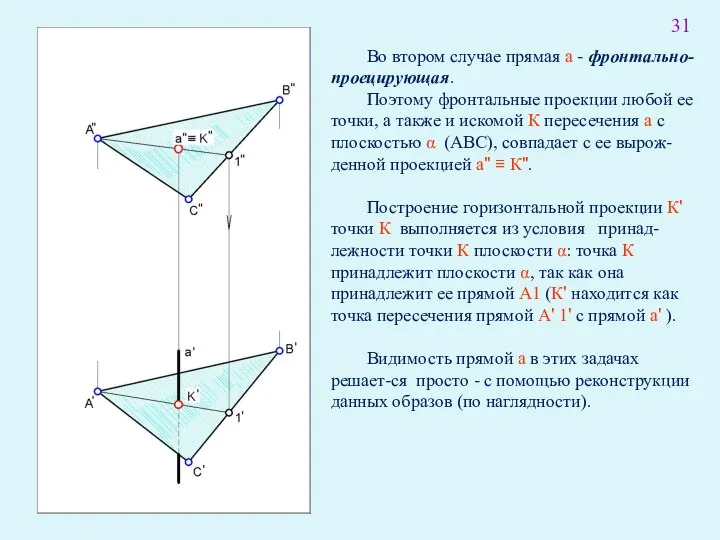
- 45. Во втором случае прямая а - фронтально-проецирующая. Поэтому фронтальные проекции любой ее точки, а также и
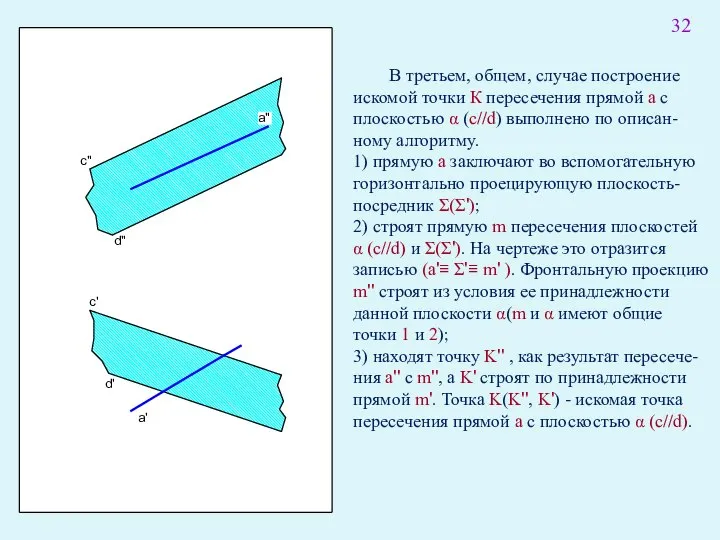
- 46. c" c' d" d' a' В третьем, общем, случае построение искомой точки К пересечения прямой а
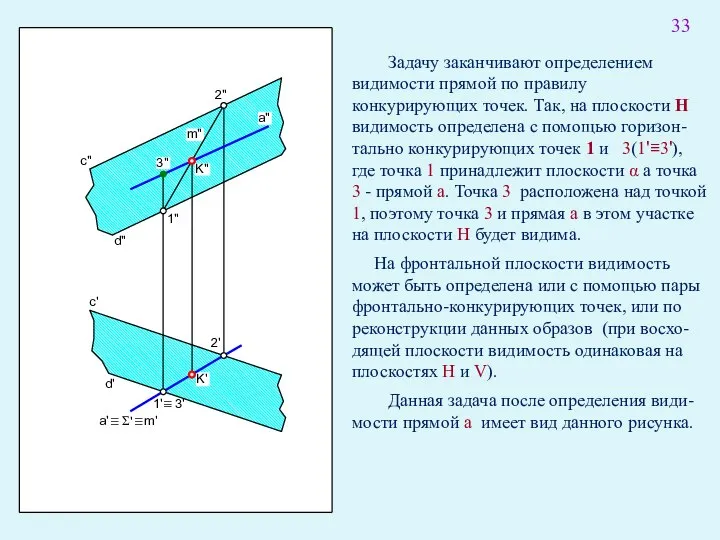
- 47. c" c' d" d' 1" 2" 2' Задачу заканчивают определением видимости прямой по правилу конкурирующих точек.
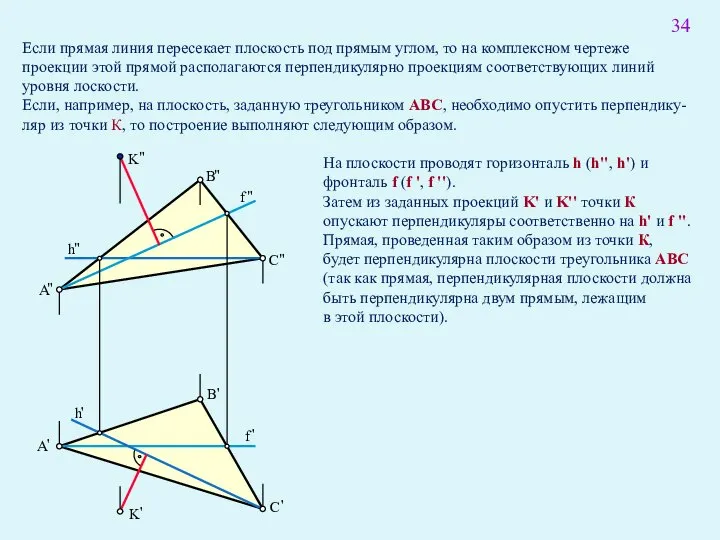
- 48. Если прямая линия пересекает плоскость под прямым углом, то на комплексном чертеже проекции этой прямой располагаются
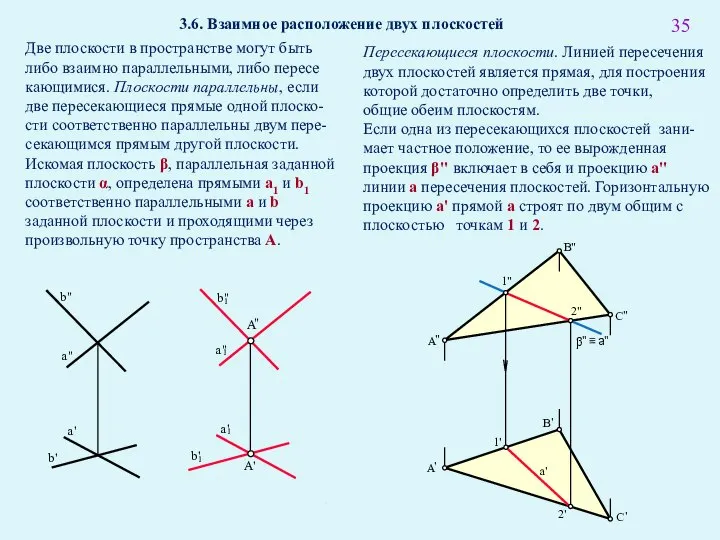
- 49. 3.6. Взаимное расположение двух плоскостей Две плоскости в пространстве могут быть либо взаимно параллельными, либо пересе
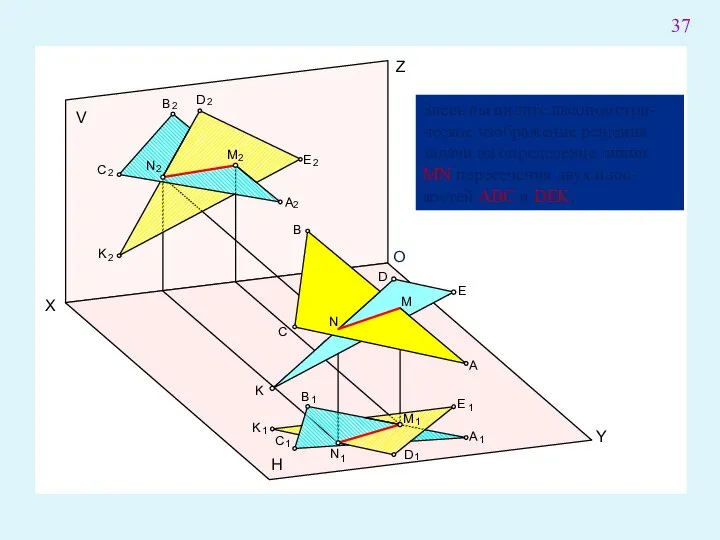
- 50. Определение линии пересечения двух плоскостей общего положения Для определения точек линии пересечения обе заданные плоскости α
- 51. Y X Z V H A B C D E K M N O Здесь вы
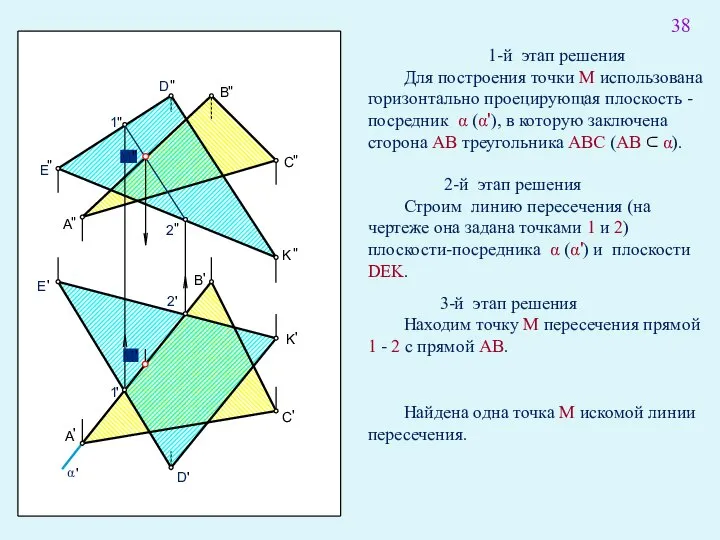
- 52. D " " E A " 1-й этап решения Для построения точки M использована горизонтально проецирующая
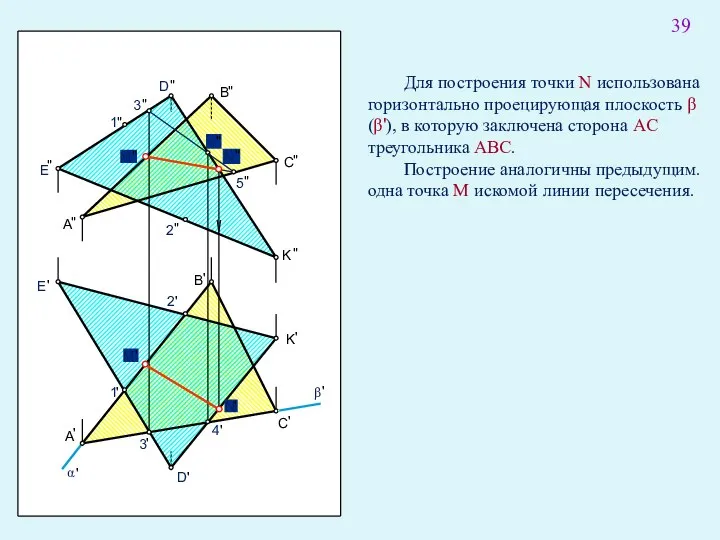
- 53. D " " E A " Для построения точки N использована горизонтально проецирующая плоскость β (β'),
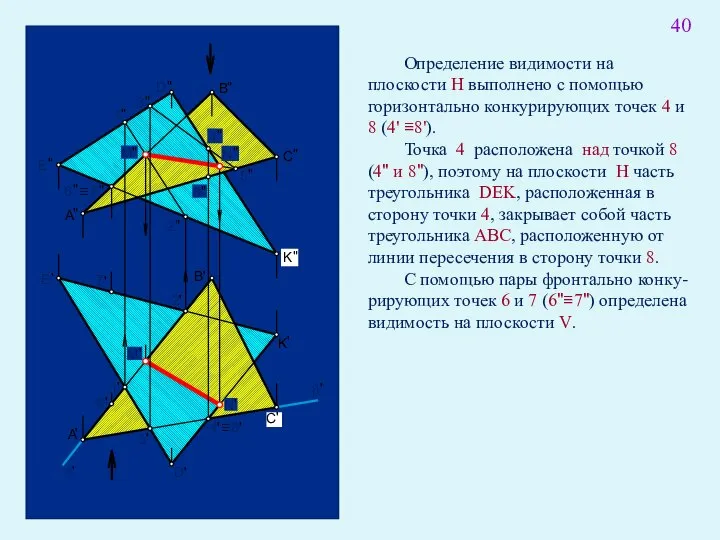
- 54. Определение видимости на плоскости H выполнено с помощью горизонтально конкурирующих точек 4 и 8 (4' ≡8').
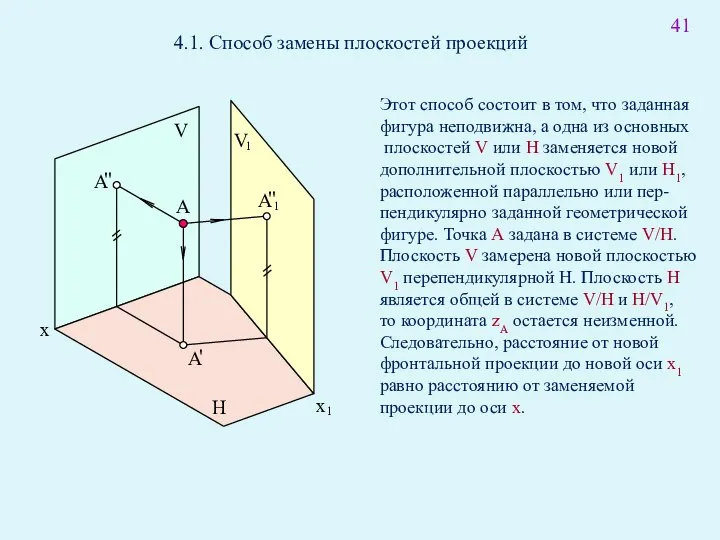
- 55. A x V H 4.1. Способ замены плоскостей проекций Этот способ состоит в том, что заданная
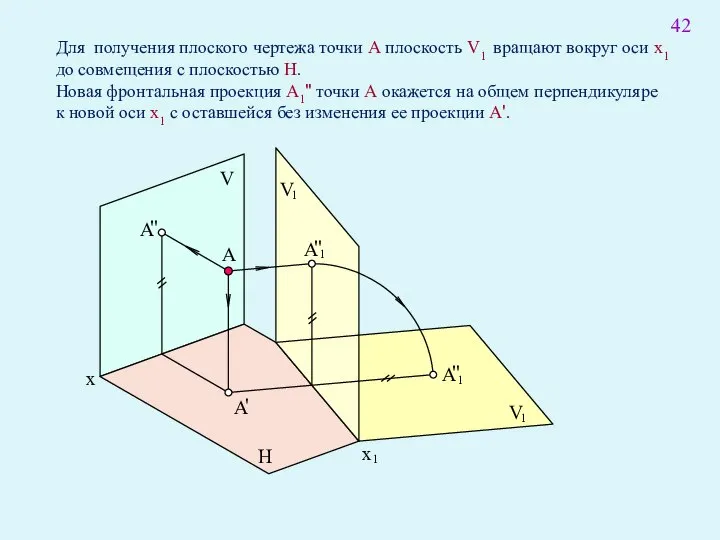
- 56. A x V H x 1 V 1 A ' A " 1 1 V 1
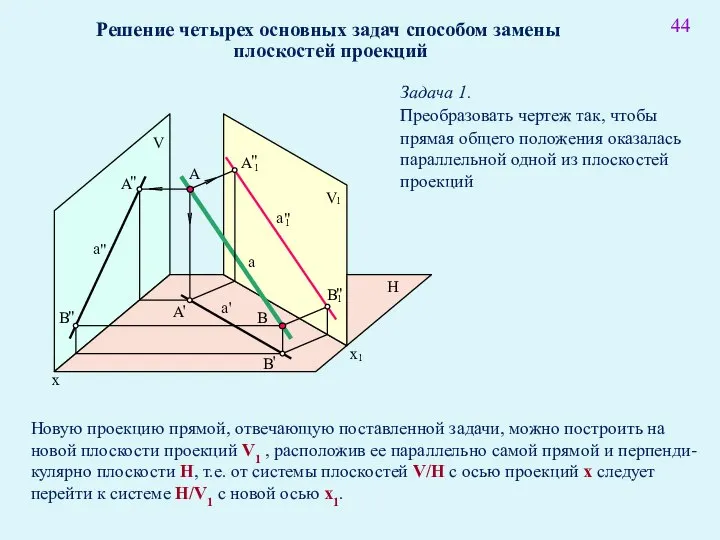
- 57. 44 Решение четырех основных задач способом замены плоскостей проекций Задача 1. Преобразовать чертеж так, чтобы прямая
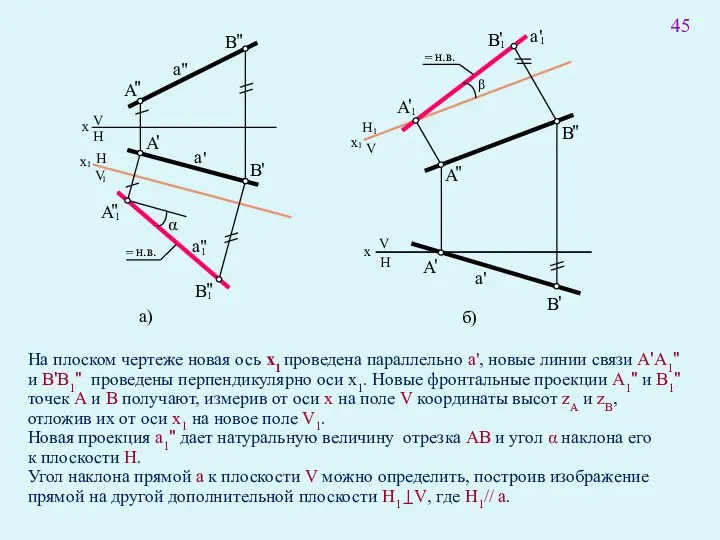
- 58. 45 На плоском чертеже новая ось x1 проведена параллельно a', новые линии связи A'A1" и B'B1"
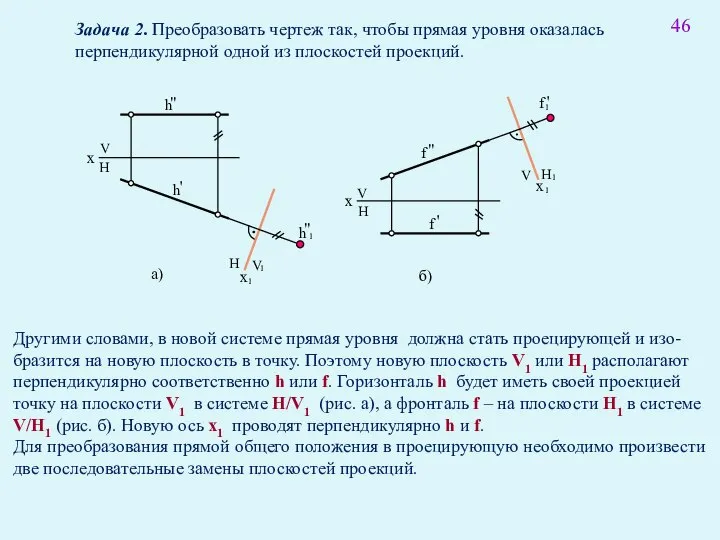
- 59. 46 x H H H V V x V а) б) Другими словами, в новой системе
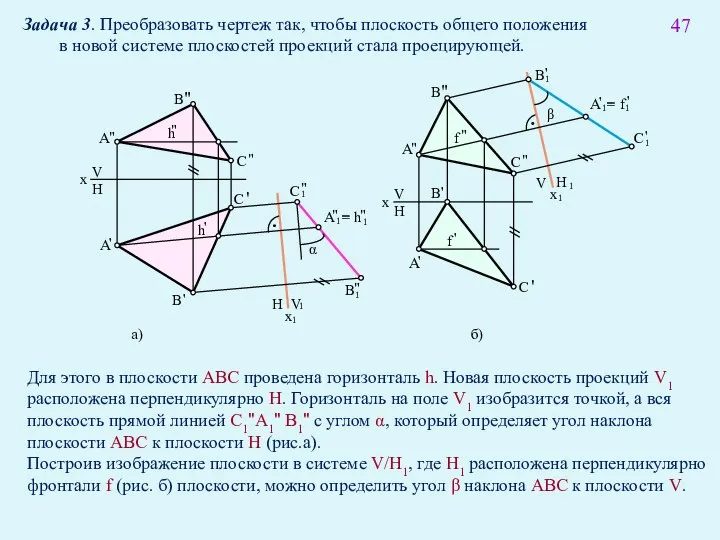
- 60. 47 x H V H H V V x β α а) б) Задача 3. Преобразовать
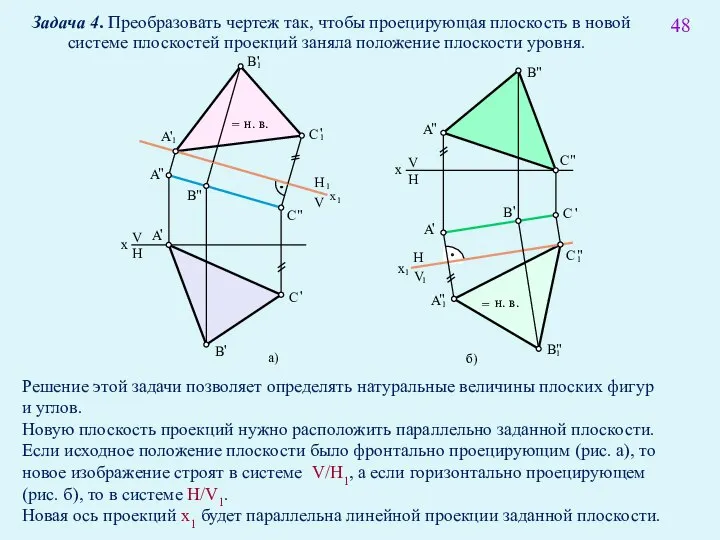
- 61. 48 V H x H V x H V а) б) Задача 4. Преобразовать чертеж так,
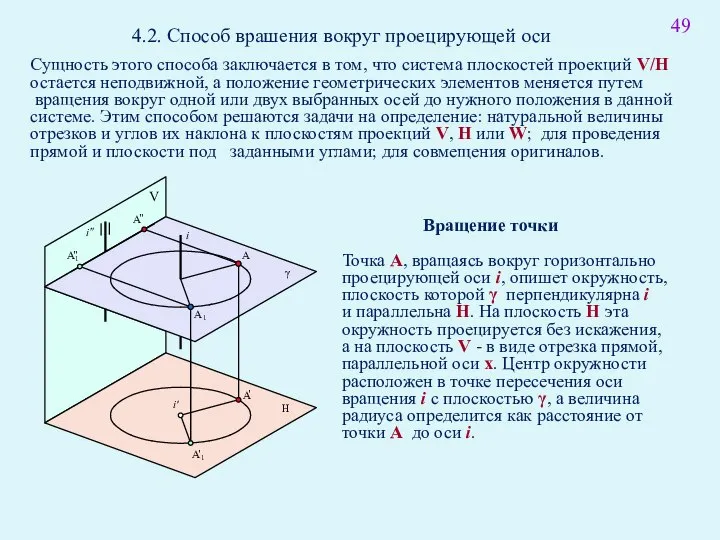
- 62. 49 4.2. Способ врашения вокруг проецирующей оси Сущность этого способа заключается в том, что система плоскостей
- 63. 51 Если ось вращения горизонтально проецирующая прямая, то точка A вращается в горизонтальной плоскости уровня γ.
- 64. 52 Вращение прямой линии Чтобы построить проекции отрезка AB, повернутого вокруг оси i на угол ϕ,
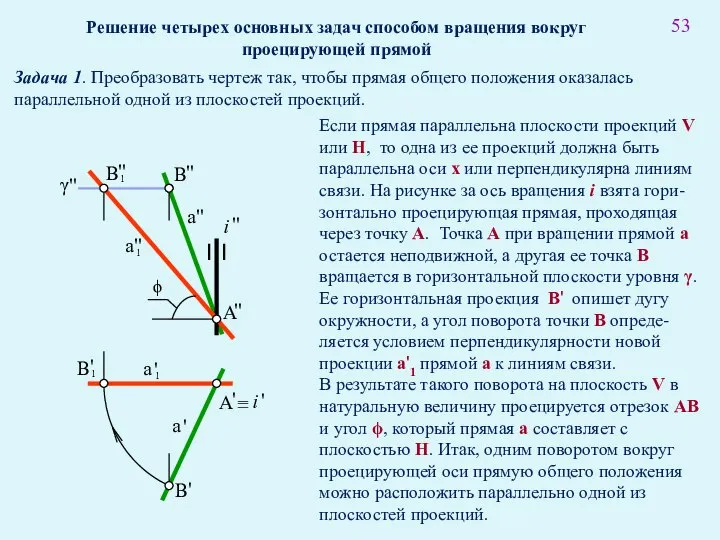
- 65. 53 Решение четырех основных задач способом вращения вокруг проецирующей прямой Задача 1. Преобразовать чертеж так, чтобы
- 66. 54 На рисинке прямая a задана фронталью, т.е. пераллельной плоскости V, поэтому за ось вращения необходимо
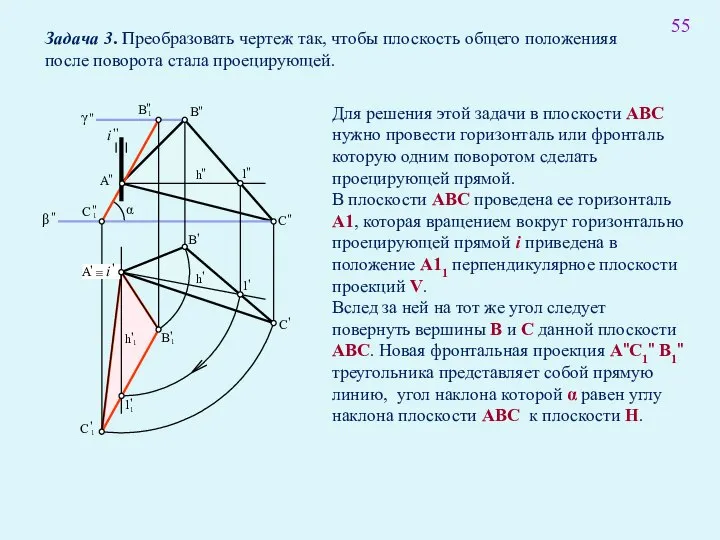
- 67. 55 Задача 3. Преобразовать чертеж так, чтобы плоскость общего положенияя после поворота стала проецирующей. Для решения
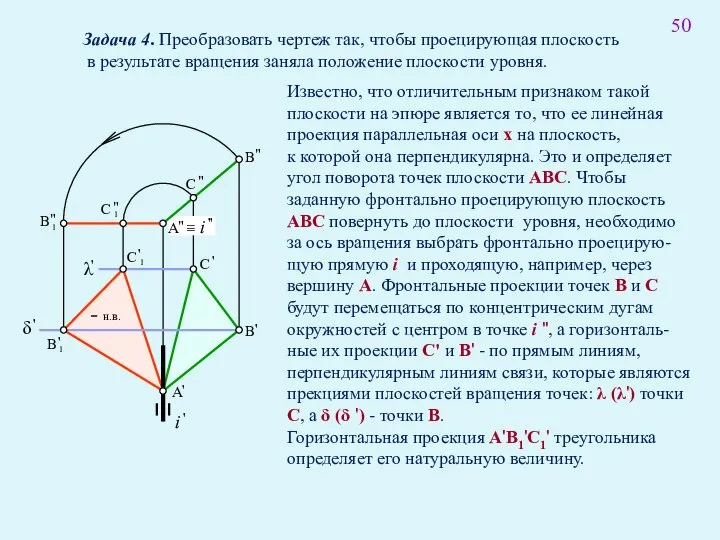
- 68. 50 Задача 4. Преобразовать чертеж так, чтобы проецирующая плоскость в результате вращения заняла положение плоскости уровня.
- 70. Скачать презентацию
















 Баскетбол. Этапы развития баскетбола
Баскетбол. Этапы развития баскетбола Aztec
Aztec Презентация "Альфред Хичкок" - скачать презентации по МХК
Презентация "Альфред Хичкок" - скачать презентации по МХК Проект разработки портала турфирмы
Проект разработки портала турфирмы  Основы разработки тестовых сценариев
Основы разработки тестовых сценариев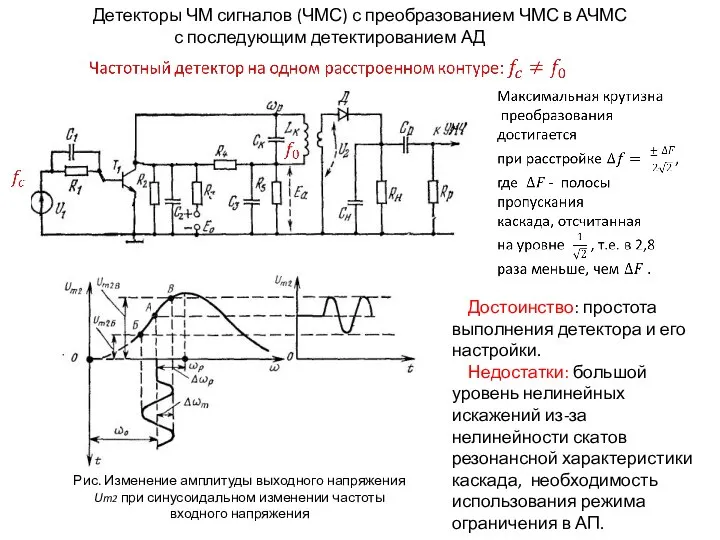 Детекторы ЧМ сигналов (ЧМС) с преобразованием ЧМС в АЧМС с последующим детектированием АД
Детекторы ЧМ сигналов (ЧМС) с преобразованием ЧМС в АЧМС с последующим детектированием АД СПЕЦИАЛЬНАЯ ОЦЕНКА УСЛОВИЙ ТРУДА КАК ИНСТРУМЕНТ СОВЕРШЕНСТВОВАНИЯ УСЛОВИЙ И ОХРАНЫ ТРУДА Задачи федеральной инспекции труда
СПЕЦИАЛЬНАЯ ОЦЕНКА УСЛОВИЙ ТРУДА КАК ИНСТРУМЕНТ СОВЕРШЕНСТВОВАНИЯ УСЛОВИЙ И ОХРАНЫ ТРУДА Задачи федеральной инспекции труда  Период ветхозаветных праотцев
Период ветхозаветных праотцев Презентация на тему "О развитии исследовательской деятельности учащихся на уроках химии и во внеурочное время" - скачать през
Презентация на тему "О развитии исследовательской деятельности учащихся на уроках химии и во внеурочное время" - скачать през Проверенные методы онлайн продвижения бренда. Каналы, отклик, подводные камни. Докладчик: Роман Славка Конференция Интернет-мар
Проверенные методы онлайн продвижения бренда. Каналы, отклик, подводные камни. Докладчик: Роман Славка Конференция Интернет-мар Фитнес-линейка HUDORA
Фитнес-линейка HUDORA Лениград
Лениград  Метод прогнозных сценариев в исследовании социально-экономических и политических процессов
Метод прогнозных сценариев в исследовании социально-экономических и политических процессов Управление командой проекта
Управление командой проекта Мы сами сказку создаем
Мы сами сказку создаем Презентация "Ключ к пониманию бизнеса" - скачать презентации по Экономике
Презентация "Ключ к пониманию бизнеса" - скачать презентации по Экономике Оптимизация процесса технико-тактической подготовки высококвалифицированных самбистов перед ответственными соревнованиями
Оптимизация процесса технико-тактической подготовки высококвалифицированных самбистов перед ответственными соревнованиями Біоетичні проблеми смерті: аутопсія, смерть головного мозку, евтаназія. Трансплантація органів та тканин
Біоетичні проблеми смерті: аутопсія, смерть головного мозку, евтаназія. Трансплантація органів та тканин Виды административных наказаний, их общая характеристика Выполнила: студентка 2 курса ЭФ, группы Э091 Т.В.Дивейкус
Виды административных наказаний, их общая характеристика Выполнила: студентка 2 курса ЭФ, группы Э091 Т.В.Дивейкус Буратіно. Вироби з дерева, різьба по дереву та меблеві вироби
Буратіно. Вироби з дерева, різьба по дереву та меблеві вироби Условия для создания образовательной среды для взрослых на приходе
Условия для создания образовательной среды для взрослых на приходе Выбор стиля для проектирования
Выбор стиля для проектирования МОУ «Дмитриевская средняя общеобразовательная школа» Художник Николай Богданов - Бельский
МОУ «Дмитриевская средняя общеобразовательная школа» Художник Николай Богданов - Бельский КЕМ БЫТЬ??? УЧИТЕЛЬ: КУЛИКОВА ИРИНА ЮРЬЕВНА ГОУ СОШ №929 САО МОСКВА
КЕМ БЫТЬ??? УЧИТЕЛЬ: КУЛИКОВА ИРИНА ЮРЬЕВНА ГОУ СОШ №929 САО МОСКВА Параллельные архитектуры с неоднородным доступом к памяти. NUMA-системы
Параллельные архитектуры с неоднородным доступом к памяти. NUMA-системы  Определение поставщиков путем проведения электронного аукциона. Тема 10.2
Определение поставщиков путем проведения электронного аукциона. Тема 10.2 СУТЬ ТА ХАРАКТЕРНІ РИСИ МІЖНАРОДНОГО МЕНЕДЖМЕНТУ
СУТЬ ТА ХАРАКТЕРНІ РИСИ МІЖНАРОДНОГО МЕНЕДЖМЕНТУ Презентация "Приматы" - скачать презентации по Экономике
Презентация "Приматы" - скачать презентации по Экономике