Содержание
- 2. Рекомендуемая литература Начертательная геометрия Учеб. для вузов / Н. Н. Крылов, Г. С. Иконникова, В. JI.
- 3. Программы дополнительного образования Дистанционное обучение Портал дистанционного обучения СПбГАСУ Кафедры Начертательной геометрии и инженерной графики Гостевой
- 4. ЛЕКЦИЯ №1
- 5. Начертательная геометрия – раздел геометрии, в котором пространственные фигуры, а также методы решения и исследования пространственных
- 6. Начертательная геометрия изучает пространственные формы реальных объектов, отношения между ними с помощью их изображений на плоскости,
- 7. Задачи начертательной геометрии Изучение способов построения изображений; Изучение способов определения форм и размеров предмета с помощью
- 8. Исторические сведения
- 9. Изображение геометрической фигуры пространства на плоскости, выполненное по установленным стандартами правилам, называют чертежом. Чертеж – международный
- 10. Базовые геометрические элементы начертательной геометрии Поверхность – непрерывное двумерное множество точек. Измерения : длина, ширина, площадь.
- 11. Основные отношения: точка лежит на прямой на плоскости, точка лежит между двумя другими. Евклидова геометрия -
- 12. В современном изложении систему аксиом Евклидовой геометрии разбивают на следующие пять групп. 1. Аксиомы сочетания. 2.
- 13. Проективное пространство
- 14. Евклидовы плоскость и пространство, дополненные соответственно бесконечно удаленными точками, прямыми и плоскостями, называются проективными.
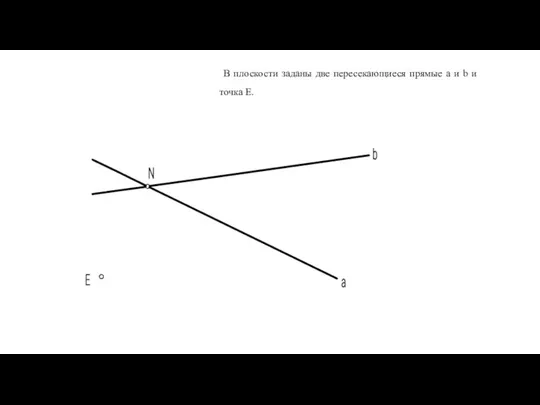
- 15. В плоскости заданы две пересекающиеся прямые a и b и точка E.
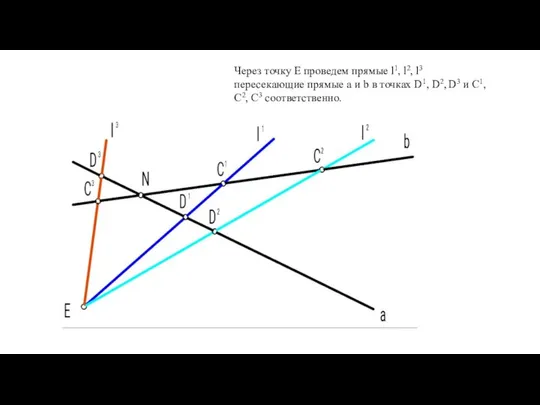
- 16. Через точку Е проведем прямые l1, l2, l3 пересекающие прямые a и b в точках D1,
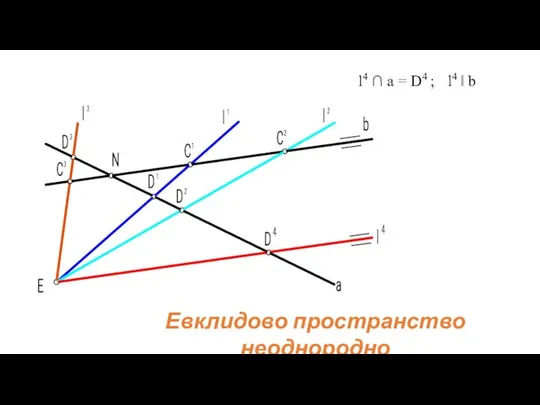
- 17. l4 ∩ a = D4 ; l4 ‖ b Евклидово пространство неоднородно
- 18. Для устранения неоднородности Евклидова пространства условно принято, что параллельные между собой прямые пересекаются в бесконечно удаленной
- 19. Евклидово пространство, дополненное несобственными элементами, называют проективным.
- 20. Метод проекций
- 21. Требования, предъявляемые к проекционному чертежу: Должен быть наглядным; Должен однозначно определять форму и положение изображаемого предмета;
- 22. Проецирование — это процесс, в результате которого получают изображения, представляющие собой проекции на плоскости. πn –
- 23. Произвольная плоскость π (.)S-центр проецирования. SA– проецирующий луч Произвольная (.)А На плоскости π проекция точки А—А'
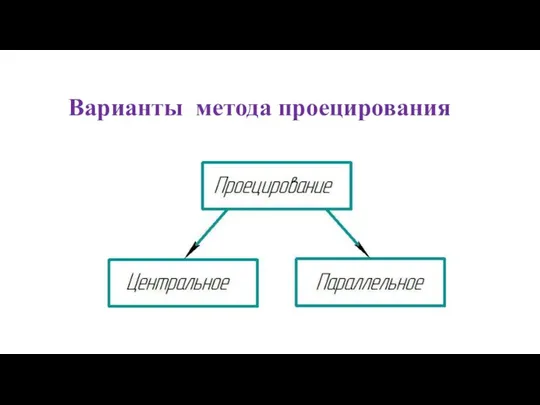
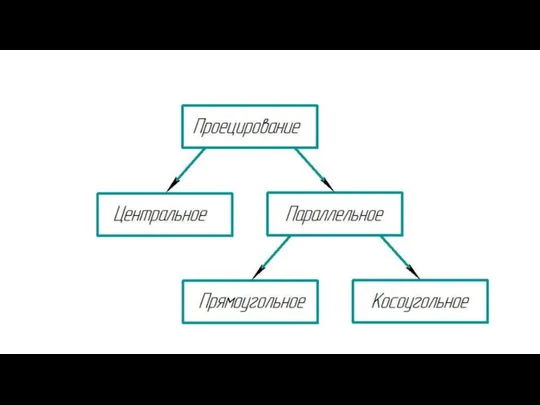
- 24. Варианты метода проецирования
- 25. S (центр проецирования) -– реальная точка. Расстояние от S до плоскости проекций πn измеримая величина. Центральное
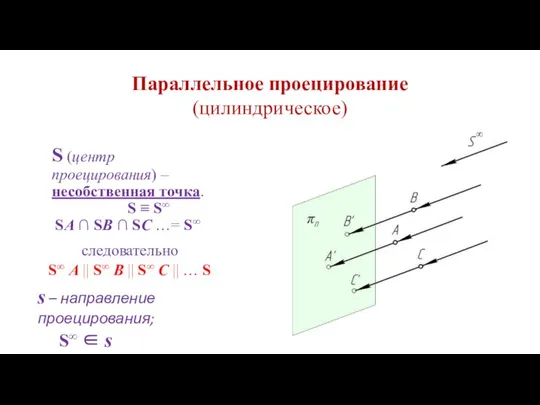
- 26. Параллельное проецирование (цилиндрическое) S (центр проецирования) – несобственная точка. S ≡ S∞ SA ∩ SB ∩
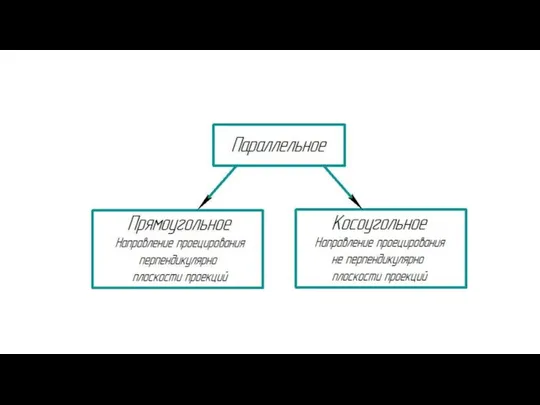
- 28. Косоугольное проецирование Прямоугольное проецирование
- 30. - перспективные проекции. Четыре основных раздела начертательной геометрии - ортогональные проекции; - проекции с числовыми отметками;
- 31. Ортогональная система двух взаимно перпендикулярных плоскостей проекции. Метод Монжа
- 32. π1 горизонтальная плоскость проекций π2 фронтальная плоскость проекций π1┴ π2 х12 - ось проекции линия пересечения
- 33. Положение 2. Плоскости проекций бесконечны и не прозрачны.
- 34. Положение 3. Ортогональные проекции точки на две взаимно перпендикулярные плоскости вполне определяют положение этой точки в
- 35. Ортогональная система трёх плоскостей проекций.
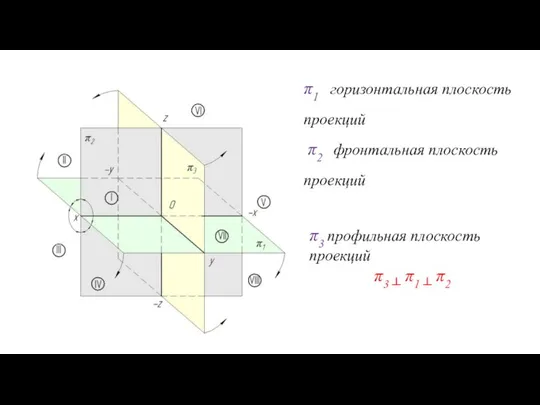
- 36. π3 профильная плоскость проекций π3 ┴ π1 ┴ π2 π1 горизонтальная плоскость проекций π2 фронтальная плоскость
- 37. Положение 6. Система трёх взаимно перпендикулярных плоскостей делит пространство на восемь частей (октантов). Х – абсцисса
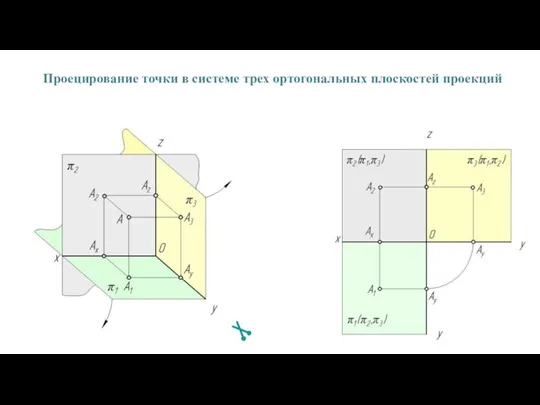
- 38. Проецирование точки в системе трех ортогональных плоскостей проекций
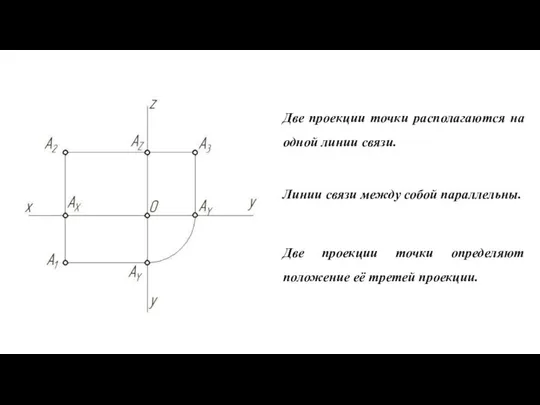
- 39. Две проекции точки располагаются на одной линии связи. Линии связи между собой параллельны. Две проекции точки
- 40. Положение 7. Если точка принадлежит плоскости проекции, то её соответствующая проекция принадлежит этой плоскости и, соответственно
- 41. Переход к безосному чертежу
- 42. Взаимное расположение прямой и точки. Положение 8. Если точка принадлежит прямой, то её проекции принадлежат соответствующим
- 43. Проецирование прямой линии
- 45. Скачать презентацию
































 Дирофиляриоз
Дирофиляриоз  Fokina_L_P_Chasti_rechi
Fokina_L_P_Chasti_rechi Ахмат Фаткуллович Лутфу́ллин
Ахмат Фаткуллович Лутфу́ллин  Презентация "Агентства социального маркетинга" - скачать презентации по Экономике
Презентация "Агентства социального маркетинга" - скачать презентации по Экономике Презентация Чартер
Презентация Чартер  Роль государства в экономике. 8 класс.
Роль государства в экономике. 8 класс. Федеральная служба по интеллектуальной собственности и патентам
Федеральная служба по интеллектуальной собственности и патентам Трудовое воспитание детей в ДОУ
Трудовое воспитание детей в ДОУ Система питания дизеля COMMON RAIL
Система питания дизеля COMMON RAIL Презентация "Город герой-Брест и Брестская крепость" - скачать презентации по МХК
Презентация "Город герой-Брест и Брестская крепость" - скачать презентации по МХК Delphi программасымен жұмыс жасау ерекшелігі және оны пайдалану тәсілдері
Delphi программасымен жұмыс жасау ерекшелігі және оны пайдалану тәсілдері Принципы механики. принцип возможных перемещений
Принципы механики. принцип возможных перемещений  развитие древнерусского права - копия
развитие древнерусского права - копия Презентация Рыбные консервы
Презентация Рыбные консервы Художественная культура европейского Просвещения: утверждение культа разума
Художественная культура европейского Просвещения: утверждение культа разума Презентация МИРОВОЕ ХОЗЯЙСТВО
Презентация МИРОВОЕ ХОЗЯЙСТВО Разработка урока по алгебре и началам анализа в 10 физико-математическом классе.
Разработка урока по алгебре и началам анализа в 10 физико-математическом классе. 8 класс АРХИТЕКТУРА Тема: Архитектурный стиль Барокко МОУ СОШ №26 Пос. Ильинский, Раменского р-на Московской области Педагог Мед
8 класс АРХИТЕКТУРА Тема: Архитектурный стиль Барокко МОУ СОШ №26 Пос. Ильинский, Раменского р-на Московской области Педагог Мед Служебно-деловой этикет
Служебно-деловой этикет In der Stadt unterwegs Berlin
In der Stadt unterwegs Berlin Чем может быть бревно - презентация для начальной школы
Чем может быть бревно - презентация для начальной школы Указ Президента РФ "О национальных целях и стратегических задачах развития Российской Федерации на период до 2024 года"
Указ Президента РФ "О национальных целях и стратегических задачах развития Российской Федерации на период до 2024 года" Октябрьская революция 1917 года
Октябрьская революция 1917 года Чековая лента
Чековая лента Фильтрование
Фильтрование  Обеспечение проведения единой государственной политики в области здравоохранения в Краснодарском крае
Обеспечение проведения единой государственной политики в области здравоохранения в Краснодарском крае Средства автоматизации
Средства автоматизации ОСНОВНЫЕ КОМПОНЕНТЫ ДРАМАТУРГИИ ФИЛЬМА
ОСНОВНЫЕ КОМПОНЕНТЫ ДРАМАТУРГИИ ФИЛЬМА