Содержание
- 2. Классификация связей. Принцип возможных перемещений (Принцип Лагранжа). Общее уравнение динамики (Принцип Даламбера -Лагранжа) Возможные перемещения системы.
- 3. КЛАССИФИКАЦИЯ СВЯЗЕЙ. 1. Связи делятся на стационарные и нестационарные. Опр. Связями называются любого вида ограничения, которые
- 4. 2. Связи делятся на геометрические и кинематические (дифференциальными). Опр. Связи, налагающие ограничения на положение (координаты) точек
- 5. По виду связей механические системы тоже разделяются на голономные (с голономными связями) и неголономные (содержащие неголономные
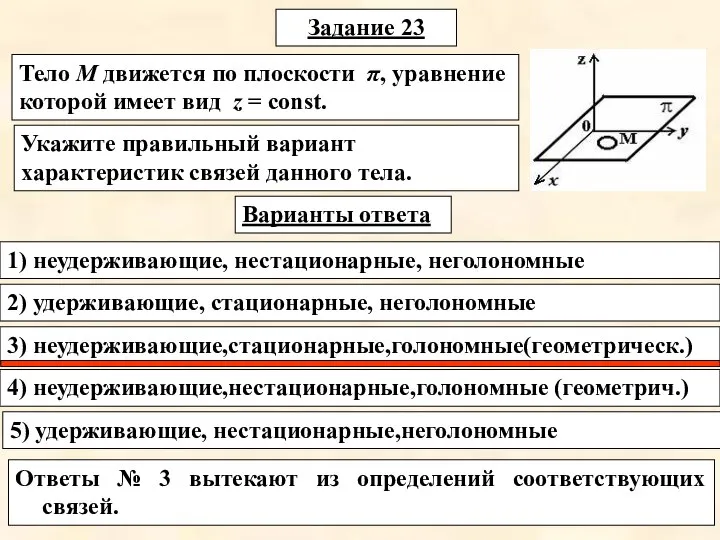
- 6. Задание 23 Варианты ответа Укажите правильный вариант характеристик связей данного тела. Тело М движется по плоскости
- 7. Действие связей можно учитывать не только вводя их реакции, но и рассматривая перемещения, которые точки механической
- 8. Возможное перемещение точки отличается от действительного прежде всего тем, что она его не совершает, а только
- 9. В общем случае система может иметь множество различных перемещений. Однако для любой из систем, которые будут
- 10. Через них можно выразить любой радиус – вектор rх rу rz Опр. Число независимых между собой
- 11. Возможная работа активной силы а возможная работа реакции обозначается символом Опр. Возможной работой называется элементарная работа,
- 12. Опр. Идеальными называются связи, для которых элементарная работа их реакций на любом возможном перемещении системы равна
- 13. Примечание. Скользящая заделка - это заделка, которая «запрещает» поворот, но не ограничивает поступательное перемещение вдоль направляющих,
- 14. Перемещения направлены по соответствующим возможным скоростям А) Определим горизонтальную реакцию в шарнире В 1. Заменим неподвижный
- 15. Поделим уравнение (1) на δs ≠ 0 и получим XВ + F cos (600) = 0.
- 16. Следовательно, т.е., связи, наложенные на балку, у ее части АС не допускают возможных перемещений. Шарнир В
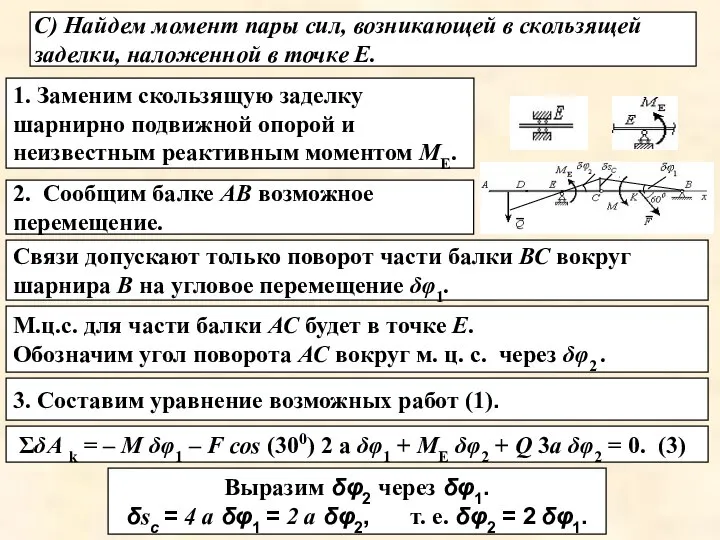
- 17. С) Найдем момент пары сил, возникающей в скользящей заделки, наложенной в точке Е. 1. Заменим скользящую
- 18. Двойная скользящая заделка – связь которая допускает любое поступательное перемещение в плоскости действия сил, но исключает
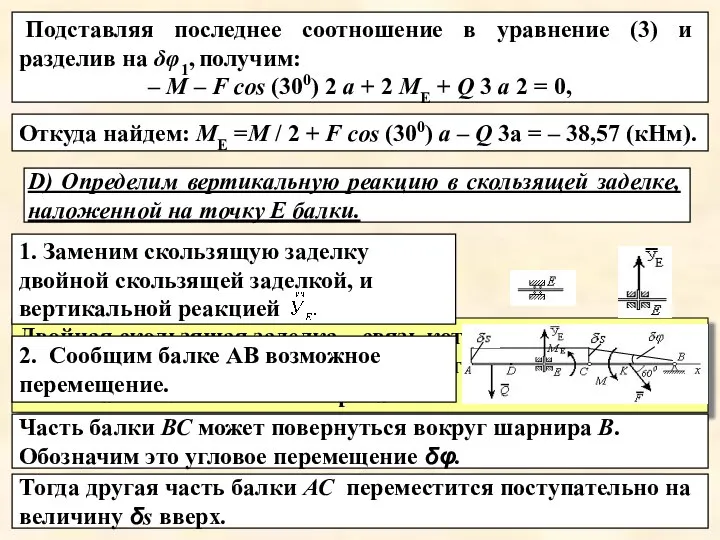
- 19. 3. Составим уравнение возможных работ (1). ΣδМk = – М δφ – F cos (300) 2а
- 20. Примечание 2. В качестве моментной точки в уравнении (3) необходимо всегда выбирать точку С, что позволит
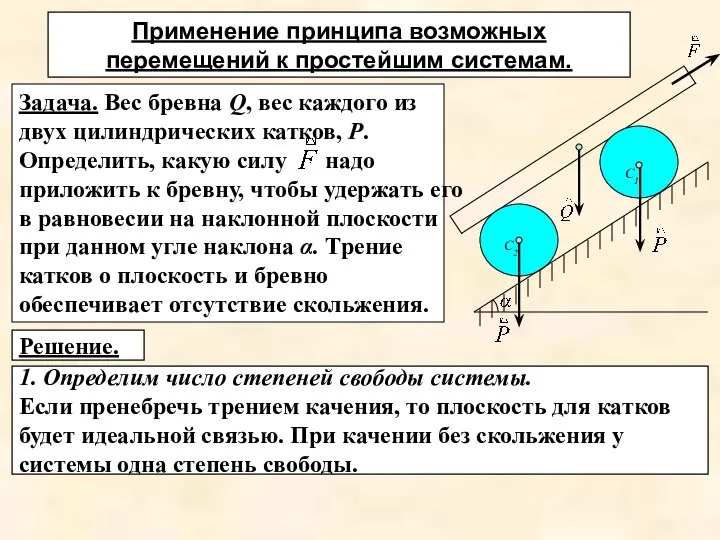
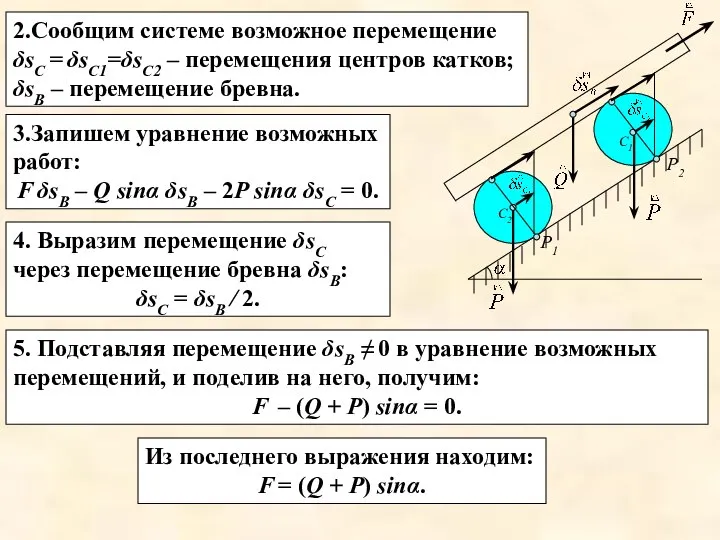
- 21. Задача. Вес бревна Q, вес каждого из двух цилиндрических катков, Р. Определить, какую силу надо приложить
- 22. 2.Сообщим системе возможное перемещение δsС = δsС1=δsС2 – перемещения центров катков; δsВ – перемещение бревна. 3.Запишем
- 23. Если ко всем точкам системы кроме действующих активных сил прибавить соответствующие силы инерции Рассмотрим систему материальных
- 24. Так как на систему наложены идеальные связи, то Тогда (3) Равенство (3) выражает принцип Даламбера –
- 25. Пример применения принцип Даламбера – Лагранжа. В подъемнике к шестерне 1, имеющей вес Р1 и радиус
- 26. 2. Присоединим к ним силу инерции груза и пары с моментами , к которым приводятся силы
- 27. Окончательно уравнение движения примет вид 4. Входящие сюда величины выразим через искомое В результате найдем окончательно
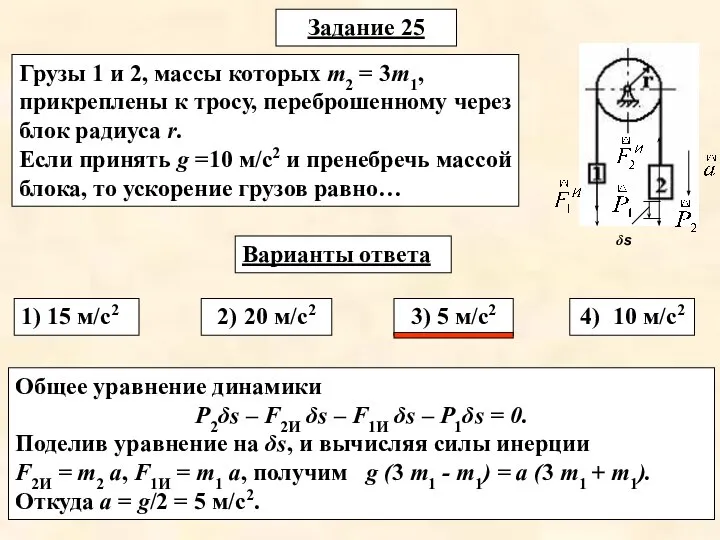
- 28. Задание 25 Варианты ответа 1) 15 м/с2 2) 20 м/с2 3) 5 м/с2 4) 10 м/с2
- 30. Скачать презентацию





















 Правоохранительная система РФ и ее задачи
Правоохранительная система РФ и ее задачи Когерентно - імпульсна РЛС
Когерентно - імпульсна РЛС Тема
Тема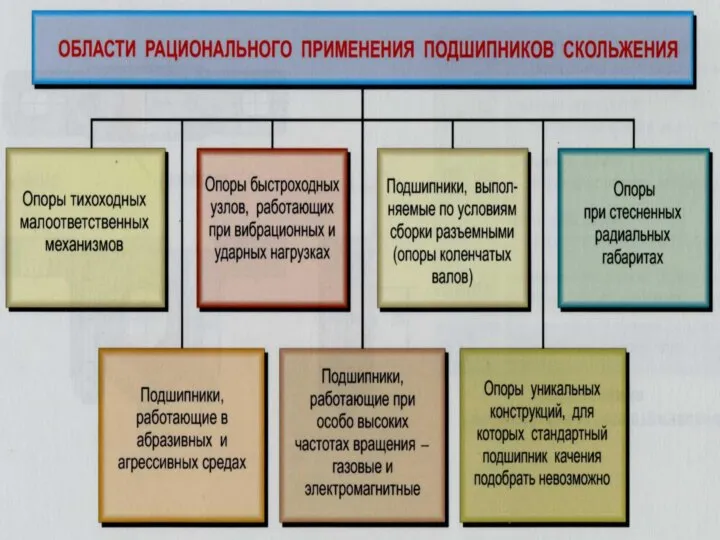 Области рационального применения подшипников скольжения
Области рационального применения подшипников скольжения Великий зодчий России
Великий зодчий России Презентация Общая характеристика исполнительного производства
Презентация Общая характеристика исполнительного производства  Серебряный век в мире искусства Валовая Г.Е.
Серебряный век в мире искусства Валовая Г.Е. Учитель начальных классов: Хомяк Надежда Атласовна МБОУ «Новоаганская ОСШ №1» ХМАО-Югра
Учитель начальных классов: Хомяк Надежда Атласовна МБОУ «Новоаганская ОСШ №1» ХМАО-Югра Типовые узлы комбинационного типа
Типовые узлы комбинационного типа Фундаменты многоэтажных зданий
Фундаменты многоэтажных зданий Задачи и механизм обеспечения национальной технологической безопасности Подготовил Ивантей М.И. Группа Т-093
Задачи и механизм обеспечения национальной технологической безопасности Подготовил Ивантей М.И. Группа Т-093  Никах - обряд бракосочетания
Никах - обряд бракосочетания Рисуем куб - презентация для начальной школы_
Рисуем куб - презентация для начальной школы_ Общее устройство автомобиля
Общее устройство автомобиля Археологічний музей Іракліону
Археологічний музей Іракліону ПРИОБРЕТЕНИЕ МУНИЦИПАЛЬНЫМИ ОБРАЗОВАНИЯМИ ПРАВА СОБСТВЕННОСТИ НА БЕСХОЗЯЙНЫЕ НЕДВИЖИМЫЕ ВЕЩИ И НАСЛЕДОВАНИЕ ВЫМОРОЧНОГО ИМУ
ПРИОБРЕТЕНИЕ МУНИЦИПАЛЬНЫМИ ОБРАЗОВАНИЯМИ ПРАВА СОБСТВЕННОСТИ НА БЕСХОЗЯЙНЫЕ НЕДВИЖИМЫЕ ВЕЩИ И НАСЛЕДОВАНИЕ ВЫМОРОЧНОГО ИМУ Презентация Педагогика в средние века и эпоху возрождения
Презентация Педагогика в средние века и эпоху возрождения Загальні правила підбору посуду та подачі чаю
Загальні правила підбору посуду та подачі чаю Дискретный характер социокультурной истории России Выполнили:
Дискретный характер социокультурной истории России Выполнили: Конфаундинг
Конфаундинг Гражданские права и обязанности
Гражданские права и обязанности  Политические партии
Политические партии Подготовка к КР №1. Kennenlernen (Знакомство)
Подготовка к КР №1. Kennenlernen (Знакомство) «Восточная» деловая культура. Япония
«Восточная» деловая культура. Япония Я і мая сям’я. Мае сваякі. (Тэма 6)
Я і мая сям’я. Мае сваякі. (Тэма 6) Классы. Базовый класс
Классы. Базовый класс Презентация Инновационная экономика Нидерландов
Презентация Инновационная экономика Нидерландов  УСТОЙЧИВОСТЬ СИСТЕМ УПРАВЛЕНИЯ
УСТОЙЧИВОСТЬ СИСТЕМ УПРАВЛЕНИЯ