Содержание
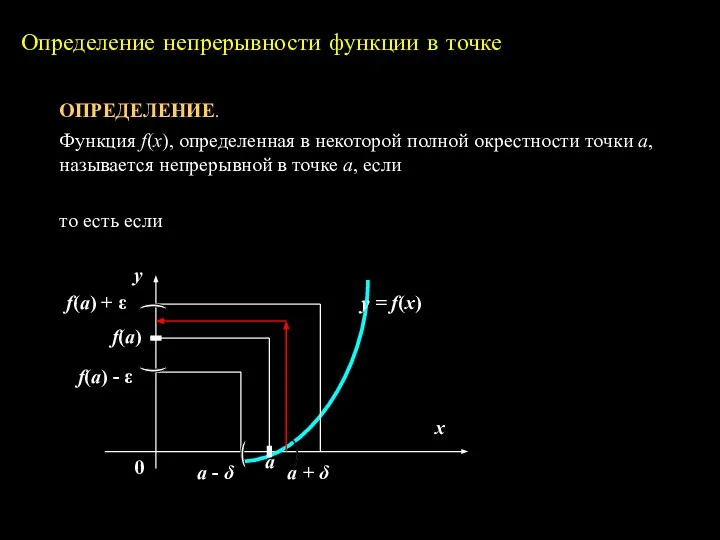
- 2. Определение непрерывности функции в точке ОПРЕДЕЛЕНИЕ. Функция f(x), определенная в некоторой полной окрестности точки а, называется
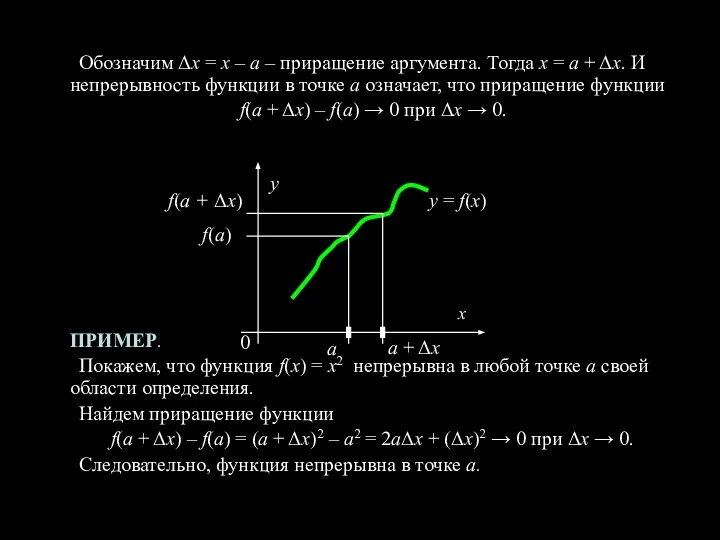
- 3. Обозначим Δх = х – а – приращение аргумента. Тогда х = а + Δх. И
- 4. ОПРЕДЕЛЕНИЕ. Функция f(x), определенная в левой полуокрестности точки а, называется непрерывной в точке а слева, если
- 5. Точки разрыва Пусть функция f(x), определена в некоторой проколотой окрестности точки а. Точка а называется точкой
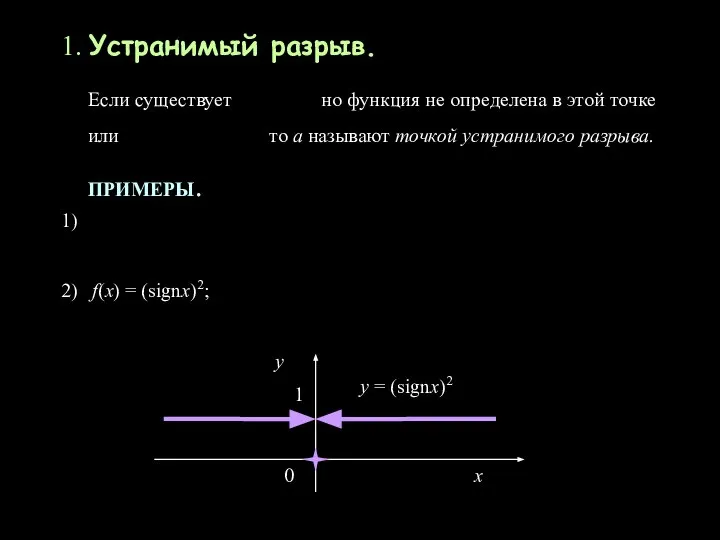
- 6. 1. Устранимый разрыв. Если существует но функция не определена в этой точке или то а называют
- 7. 2. Разрыв первого рода. Если в точке а существуют но f (a - 0) ≠ f
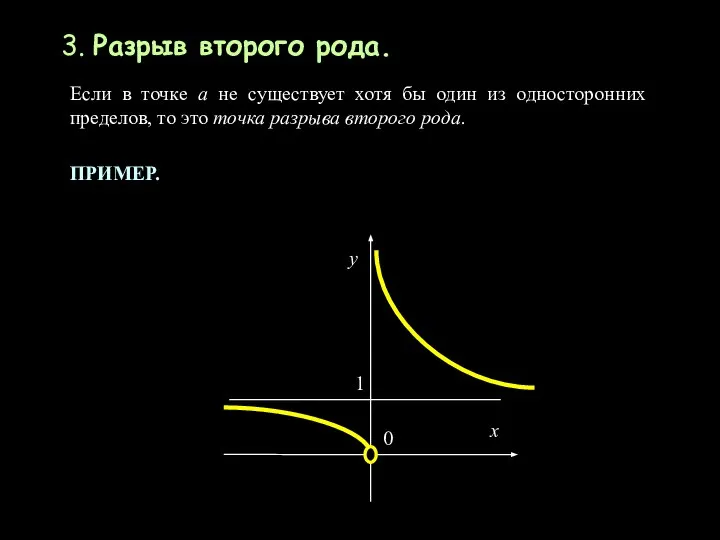
- 8. 3. Разрыв второго рода. Если в точке а не существует хотя бы один из односторонних пределов,
- 9. Свойства функций, непрерывных в точке Если функция непрерывна в точке а, то существует такая окрестность этой
- 10. Доказательство. Свойства 1 – 3 являются следствием определения непрерывности и соответствующих свойств пределов функции. Докажем свойство
- 11. Теоремы о функциях, непрерывных на отрезке. ОПРЕДЕЛЕНИЕ. Функция f(x) называется непрерывной на отрезке [a, b], если
- 12. Доказательство. Предположим, что функция не ограничена сверху на отрезке, т.е. для любого числа n∈Ν найдется xn∈[a,
- 13. ЗАМЕЧАНИЯ. 1) Теорема не верна в случае интервала, а не отрезка. Например, функция f(x)=1/х непрерывна на
- 14. О достижимости функцией, непрерывной на отрезке, своих точных граней ТЕОРЕМА (вторая теорема Вейерштрасса) Если f(x)∈C[a, b],
- 15. Эта функция непрерывна на отрезке, а значит и ограничена сверху на этом отрезке, то есть существует
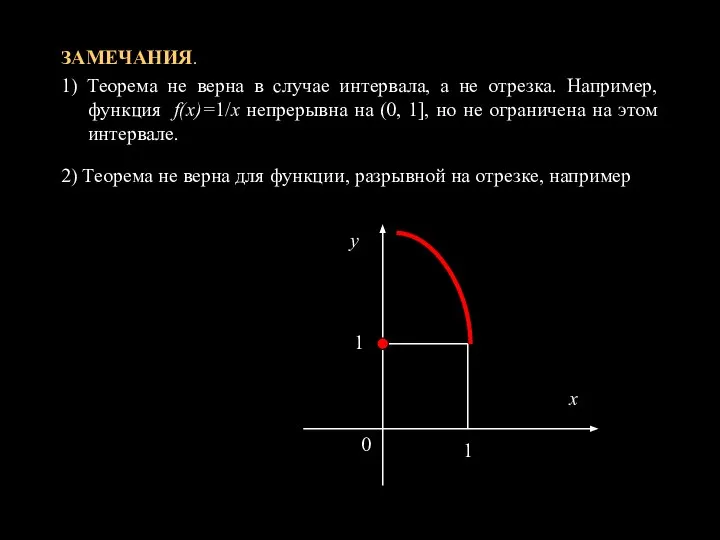
- 16. ЗАМЕЧАНИЯ. 1)Теорема не верна в случае интервала, а не отрезка. Например, функция f(x)= х непрерывна на
- 18. Скачать презентацию










 Урок изобразительного искусства в 4 классе Учитель изобразительного искусства и черчения Вельможина Е.И.
Урок изобразительного искусства в 4 классе Учитель изобразительного искусства и черчения Вельможина Е.И. Анализ педагогических результатов на основе мониторинга учащихся средней школы ТИНУС ВАЛЕНТИНА МИХАЙЛОВНА учитель физической
Анализ педагогических результатов на основе мониторинга учащихся средней школы ТИНУС ВАЛЕНТИНА МИХАЙЛОВНА учитель физической Политическая система
Политическая система Управление инновациями на микроуровне (в фирме). Модели инновационных процессов и инновационной деятельности
Управление инновациями на микроуровне (в фирме). Модели инновационных процессов и инновационной деятельности Детям о пасхе
Детям о пасхе Общее устройство автомобиля
Общее устройство автомобиля WHAT IS A GOOD PROJECT? REGIONAL DEVELOPMENT
WHAT IS A GOOD PROJECT? REGIONAL DEVELOPMENT Презентация на тему "Основы православной культуры Культура и религия"
Презентация на тему "Основы православной культуры Культура и религия" Производительность комплекса систем Простой подход к разработке методики тестирования
Производительность комплекса систем Простой подход к разработке методики тестирования Оптимизация. Использование алгоритмов
Оптимизация. Использование алгоритмов Почки. Водно-солевой гомеостаз
Почки. Водно-солевой гомеостаз  Печь с вихревым дожигателем дымовых газов. Проект
Печь с вихревым дожигателем дымовых газов. Проект Оценка качества преподавательской деятельности
Оценка качества преподавательской деятельности Технологии ГИС в ОАО Татнефть
Технологии ГИС в ОАО Татнефть Карданные передачи
Карданные передачи Печатающие устройства
Печатающие устройства 5_java_float
5_java_float Константин Дмитриевич Ушинский Выполнила студентка 2 курса РГПУ им.Герцена факультета социальных наук по направлению «Обществов
Константин Дмитриевич Ушинский Выполнила студентка 2 курса РГПУ им.Герцена факультета социальных наук по направлению «Обществов Поход №2
Поход №2 Karneval der Kulturen in Berlin-Kreuzberg
Karneval der Kulturen in Berlin-Kreuzberg Русская икона
Русская икона Профессионально-общественная аккредитация образовательных программ, основанных на профессиональных стандарта
Профессионально-общественная аккредитация образовательных программ, основанных на профессиональных стандарта Презентация на тему "батьківські збори 2015" - скачать презентации по Педагогике
Презентация на тему "батьківські збори 2015" - скачать презентации по Педагогике Керечан Ганна Іванівна - презентация для начальной школы
Керечан Ганна Іванівна - презентация для начальной школы ПРОИЗВОДСТВЕННЫЙ ШУМ И ЕГО ВОЗДЕЙСТВИЕ НА ЧЕЛОВЕКА Выполнили студенты группы Т-111 Васильев Станислав и Бобырь Алексей.
ПРОИЗВОДСТВЕННЫЙ ШУМ И ЕГО ВОЗДЕЙСТВИЕ НА ЧЕЛОВЕКА Выполнили студенты группы Т-111 Васильев Станислав и Бобырь Алексей. Биография Д.И. Менделеева в датах
Биография Д.И. Менделеева в датах Презентация на тему "Методы воспитания" - скачать презентации по Педагогике
Презентация на тему "Методы воспитания" - скачать презентации по Педагогике Технические нормативные правовые акты
Технические нормативные правовые акты