Содержание
- 2. О нулях непрерывной на отрезке функции ТЕОРЕМА Если f(x)∈C[a, b] и принимает на концах отрезка значения
- 3. Доказательство. Пусть, для определенности, f(a) 0. Разобьем отрезок [a, b] пополам. Если f((a+ b)/2)= 0 ,
- 4. Продолжая этот процесс, получим: либо через конечное число шагов найдется точка ξ∈(a, b), такая что f(ξ)=
- 5. О промежуточных значениях непрерывной на отрезке функции ТЕОРЕМА Если f(x)∈C[a,b] и f(a)=A, f(b)=B, причем А ≠Β,
- 6. СЛЕДСТВИЕ. Если f(x)∈C[a, b], то множеством значений, принимаемых функцией на [a, b] , является отрезок [m,
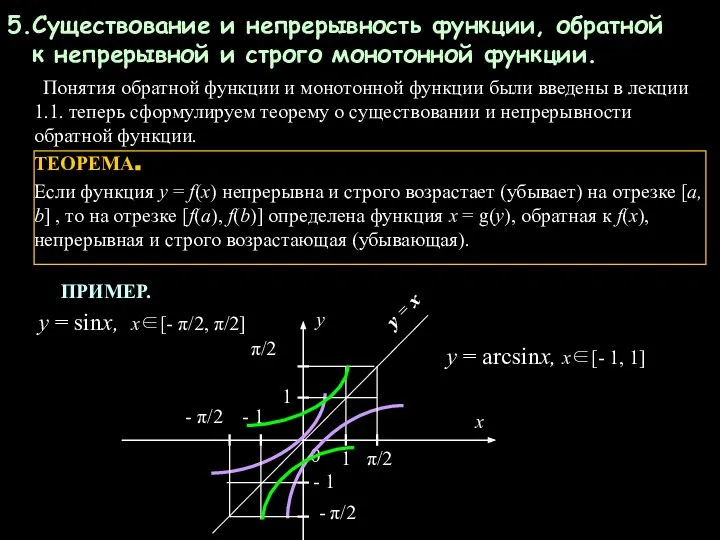
- 7. Существование и непрерывность функции, обратной к непрерывной и строго монотонной функции. Понятия обратной функции и монотонной
- 8. Непрерывность элементарных функций. МНОГОЧЛЕНЫ И ДРОБНО-РАЦИОНАЛЬНЫЕ ФУНКЦИИ. Любой многочлен степени n Pn(x) = anxn +…+a1x+a0 ,
- 9. Дробно-рациональная функция, то есть функция вида где Pn(x) – многочлен степени n, Qm(x) – многочлен степени
- 10. ТРИГОНОМЕТРИЧЕСКИЕ И ОБРАТНЫЕ ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ. Функции у = sinx и y = cosx непрерывны на R.
- 11. Функция у = tgx непрерывна, если х ≠ π/2+πn; Функция у = ctgx непрерывна, если х
- 12. ПОКАЗАТЕЛЬНАЯ И ЛОГАРИФМИЧЕСКАЯ ФУНКЦИИ. Показательная функция у = ах, где 0 1, непрерывна на R. Доказательство.
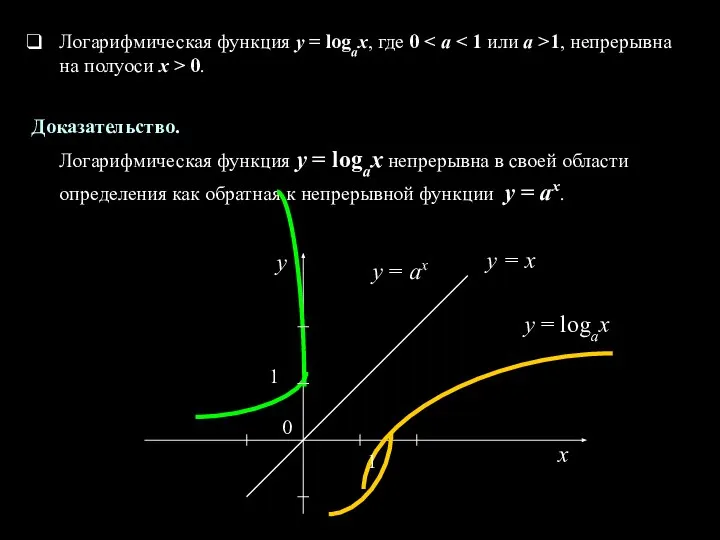
- 13. Логарифмическая функция y = logax, где 0 1, непрерывна на полуоси х > 0. Доказательство. Логарифмическая
- 14. ГИПЕРБОЛИЧЕСКИЕ ФУНКЦИИ. - гиперболический синус, непрерывен на R. - гиперболический косинус, непрерывен на R. – гиперболический
- 15. СТЕПЕННАЯ ФУНКЦИЯ. Степенная функция у = хα, α ∈ R, определенная для всех х > 0,
- 16. ЗАМЕЧАНИЕ. При рассмотрении степенной функции предполагалось, что х > 0, так как при х ≤ 0
- 17. КЛАСС ЭЛЕМЕНТАРНЫХ ФУНКЦИЙ. Класс функций, состоящий из многочленов, показательных функций, логарифмических функций, тригонометрических функций и обратных
- 19. Скачать презентацию
![О нулях непрерывной на отрезке функции ТЕОРЕМА Если f(x)∈C[a, b] и](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1296487/slide-1.jpg)
![Доказательство. Пусть, для определенности, f(a) 0. Разобьем отрезок [a, b] пополам.](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1296487/slide-2.jpg)

![О промежуточных значениях непрерывной на отрезке функции ТЕОРЕМА Если f(x)∈C[a,b] и](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1296487/slide-4.jpg)
![СЛЕДСТВИЕ. Если f(x)∈C[a, b], то множеством значений, принимаемых функцией на [a,](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1296487/slide-5.jpg)









 Продажа дачного участка с двумя домами
Продажа дачного участка с двумя домами Открытка для папы
Открытка для папы Симметрия
Симметрия Эзофагопластика
Эзофагопластика Определение отверстия моста. Размещение его в створе перехода. Назначение схемы моста
Определение отверстия моста. Размещение его в створе перехода. Назначение схемы моста Графики функций Работу выполнила учитель математики Серебрянская Л. А.
Графики функций Работу выполнила учитель математики Серебрянская Л. А. Курсова робота (Курсовий проект)
Курсова робота (Курсовий проект) Монтаж осветительной и силовой проводки электроучастка АО "Энергия" Мари-Турекского района. Реконструкция осветительной сет
Монтаж осветительной и силовой проводки электроучастка АО "Энергия" Мари-Турекского района. Реконструкция осветительной сет Белая береза - символ России
Белая береза - символ России Calligraphy Design
Calligraphy Design Геодезическая купольная теплица
Геодезическая купольная теплица Презентация "Айвазовский" - скачать презентации по МХК
Презентация "Айвазовский" - скачать презентации по МХК Смешанные боевые искусства (MMA)
Смешанные боевые искусства (MMA) Пишем бизнес-план? Николай Савин MD GrowthUP ns@growthup.com
Пишем бизнес-план? Николай Савин MD GrowthUP ns@growthup.com  Подростковый возраст Родительское собрание
Подростковый возраст Родительское собрание Психолого-педагогическое сопровождение учащихся групп социального риска Психолого-педагогическое сопровождение учащихся групп
Психолого-педагогическое сопровождение учащихся групп социального риска Психолого-педагогическое сопровождение учащихся групп Регби. Правила игры
Регби. Правила игры Daikin’s hot gas defrost
Daikin’s hot gas defrost Герб России
Герб России Виды танца
Виды танца Нетрадиционные формы повторительно-обобщающих уроков технологии с использованием технологии развивающих и деловых игр и компью
Нетрадиционные формы повторительно-обобщающих уроков технологии с использованием технологии развивающих и деловых игр и компью Художественная гимнастика
Художественная гимнастика Тема по самообразованию: Внедрение в учебный процесс новых технологий обучения. Учитель русского языка и литературы Потанинской
Тема по самообразованию: Внедрение в учебный процесс новых технологий обучения. Учитель русского языка и литературы Потанинской  Исковые требования. Примеры
Исковые требования. Примеры Создать Презентация Microsoft Office PowerPoint
Создать Презентация Microsoft Office PowerPoint Презентация на тему "1 сентября" - скачать презентации по Педагогике
Презентация на тему "1 сентября" - скачать презентации по Педагогике Информационные системы предприятия (ИСП)
Информационные системы предприятия (ИСП) Апаратне забезпечення інформаційних систем. Історія розвитку обчислювальної техніки. (Урок 4)
Апаратне забезпечення інформаційних систем. Історія розвитку обчислювальної техніки. (Урок 4)