Содержание
- 2. Первый замечательный предел Рассмотрим круг единичного радиуса с центром в точке О. A D B C
- 3. Так как то последнее неравенство справедливо и для Отсюда, в частности, следует, что Оценим разность: Итак,
- 4. Второй замечательный предел Напомним, что Далее покажем, что Пусть х >1. Положим n = [х]. Тогда
- 5. Найдем пределы последовательностей в левой и правой частях неравенства: Следовательно, по теореме «о двух милиционерах»
- 6. Покажем, что Пусть х Итак, мы установили, что
- 7. Замена переменной при вычислении пределов. ТЕОРЕМА. Пусть существуют Пусть, кроме того, f(x) ≠ b в некоторой
- 8. Следствия замечательных пределов. Доказать, что: 1) Доказательство. 2) Доказательство. 3) 4) Доказательство. Доказательство. Пусть arcsinx =
- 9. . 5) 6) 7) 8) Доказательство. Доказательство. Доказательство. Доказательство. e, x → 0 → lne =
- 10. . 9) 10) 11) Доказательство. Доказательство. Доказательство. Пусть y = ( 1+x)a - 1 = ealn(1+x)
- 11. Сравнение функций. Функции одного порядка. Символ «О-большое». ОПРЕДЕЛЕНИЕ. Пусть функции f(x) и g(x) определены в некоторой
- 12. Эквивалентные функции. ОПРЕДЕЛЕНИЕ. Пусть функции f(x) и g(x) определены в некоторой проколотой окрестности точки а и
- 13. Пусть α(х) – бесконечно малая при х → а функция. Тогда при х → а sin(α(х))
- 14. ТЕОРЕМА. (Замена функций на эквивалентные при вычислении предела.) Пусть f(x) ~ f1(x), g(x) ~ g1(x) при
- 15. ПРИМЕРЫ. 1) 2) Если бы мы формально заменили функции, стоящие в числителе дроби, на эквивалентные, то
- 16. Понятие функции, бесконечно малой по сравнению с другой функцией. Символ «о-малое». Пусть функции f(x) и g(x)
- 17. Свойства символа «о-малое». Отметим некоторые важные свойства символа о(g(x)), считая, что х → а, а равенства,
- 18. Асимптотическое представление функций. ТЕОРЕМА. f(x) ~ g(x) при х → а ⇔ f(x) = g(x) +
- 19. Пусть α(х) →0 при х → а. Тогда при х → а sin(α(х)) = α(х) +
- 20. ПРИМЕР. Используя асимптотические представления функций, найдем предел
- 22. Скачать презентацию


















 Презентация "Природа и архитектура" - скачать презентации по МХК
Презентация "Природа и архитектура" - скачать презентации по МХК Педагогические технологии личностно- ориентированного и развивающего обучения
Педагогические технологии личностно- ориентированного и развивающего обучения Стилевое многообразие культуры XVII-XVII вв
Стилевое многообразие культуры XVII-XVII вв Огнестойкость СК.ppt
Огнестойкость СК.ppt Икона Казанской Божьей Матери
Икона Казанской Божьей Матери История физики 2
История физики 2 Карнавал. Урок изобразительного искусства 7 класс
Карнавал. Урок изобразительного искусства 7 класс Сказка о мертвой царевне и семи богатырях - часть 1 - презентация для начальной школы
Сказка о мертвой царевне и семи богатырях - часть 1 - презентация для начальной школы Россия в XVII веке: от Смуты к утверждению самодержавно-крепостнического строя
Россия в XVII веке: от Смуты к утверждению самодержавно-крепостнического строя Виды прерываний и методы обработки современных компьютерах
Виды прерываний и методы обработки современных компьютерах Гирдромеханические передачи
Гирдромеханические передачи Сечения и разрезы
Сечения и разрезы Презентация Гегель Абсолютный идеализм
Презентация Гегель Абсолютный идеализм Привлечение клиентов в салон красоты через Интернет
Привлечение клиентов в салон красоты через Интернет Туризм в России
Туризм в России Система мероприятий по финансированию инновационной деятельности организации ООО Автоцент «Тройка»
Система мероприятий по финансированию инновационной деятельности организации ООО Автоцент «Тройка»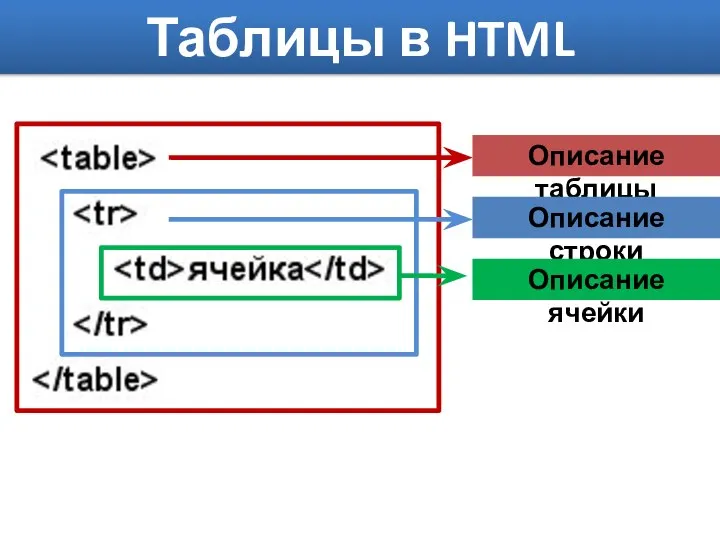 Таблицы в HTML
Таблицы в HTML Объекты гос. регистрации прав на недвижимое имущество и сделок с ним
Объекты гос. регистрации прав на недвижимое имущество и сделок с ним Национальные деловые культуры
Национальные деловые культуры Тип стрекающие
Тип стрекающие  Viera Plasma Display PC Board Recycling. Component Level Repair. Troubleshooting Hints / Common Symptoms
Viera Plasma Display PC Board Recycling. Component Level Repair. Troubleshooting Hints / Common Symptoms Образование и наука в первой половине XIX века
Образование и наука в первой половине XIX века Либерализм и его принципы. Формирование либерализма
Либерализм и его принципы. Формирование либерализма Методика расследования экологических преступлений
Методика расследования экологических преступлений  ИЗМЕНЕНИЯ В НАЛОГОВОМ ЗАКОНОДАТЕЛЬСТВЕ для физических лиц - Новые стратегии торговли - Примеры сальдирования налогов - Краткое о
ИЗМЕНЕНИЯ В НАЛОГОВОМ ЗАКОНОДАТЕЛЬСТВЕ для физических лиц - Новые стратегии торговли - Примеры сальдирования налогов - Краткое о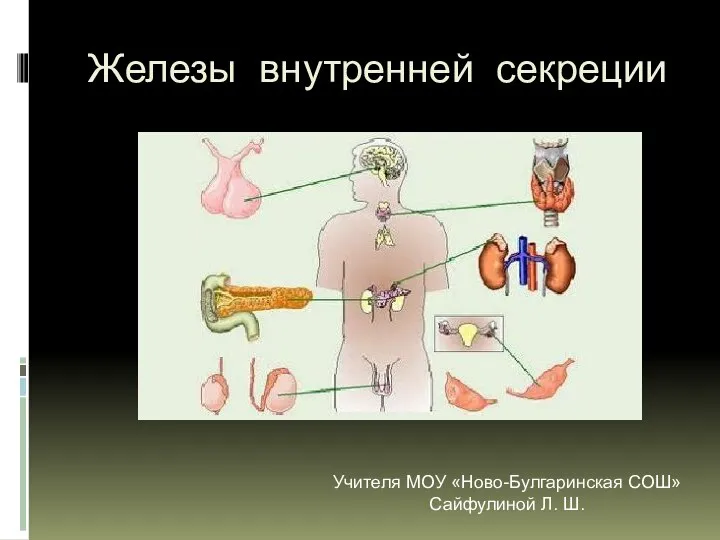 Железы внутренней секреции
Железы внутренней секреции  Интернетэкзамен в сфере профессионального образования (ФЭПО)
Интернетэкзамен в сфере профессионального образования (ФЭПО) Нуклеофильное замещение у насыщенного атома углерода
Нуклеофильное замещение у насыщенного атома углерода