Определители. Способы их вычисления

Определение: Любой квадратной матрице n-го порядка ставится в соответствие по определенному

Вычисление определителя 1-го порядка:
Пример 1.
назад

Вычисление определителя 2-го порядка:
Пример 2.
Вычислить определители следующих матриц:
2) 3)
Ответ
назад

Ответы (Пример 2):
назад

Вычисление определителя 3-го порядка (правило треугольника или правило Саррюса):
Пример 3.
назад

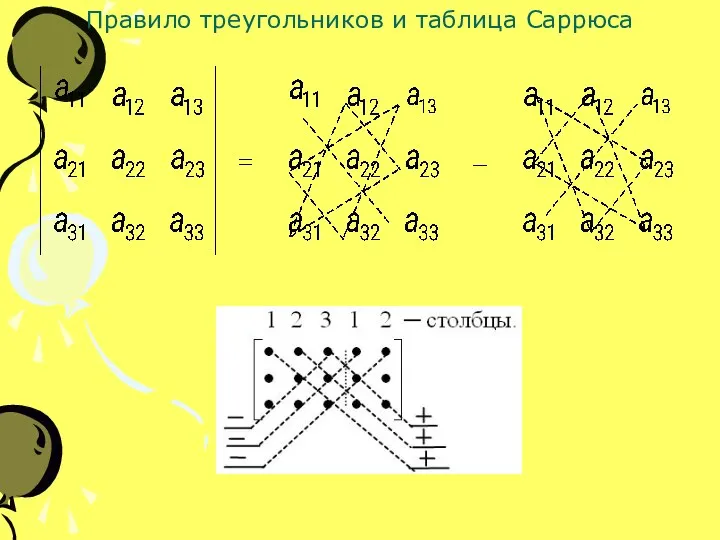
Правило треугольников и таблица Саррюса

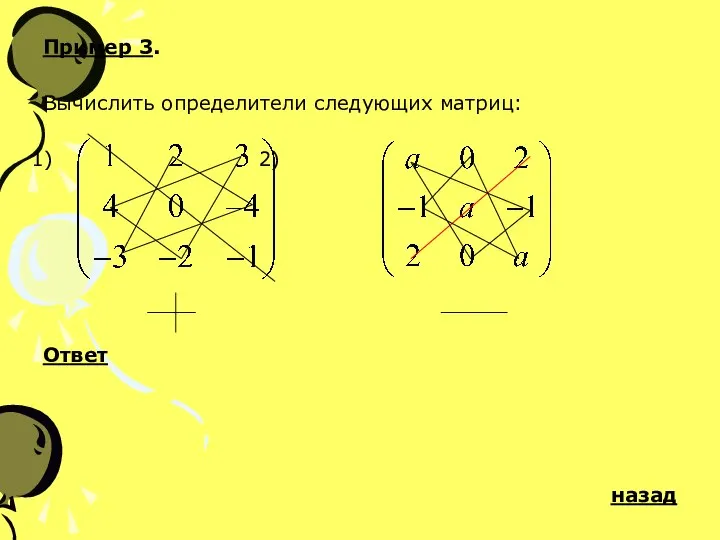
Пример 3.
Вычислить определители следующих матриц:
2)
Ответ
назад

Ответ (Пример 3):
1)
2)
назад

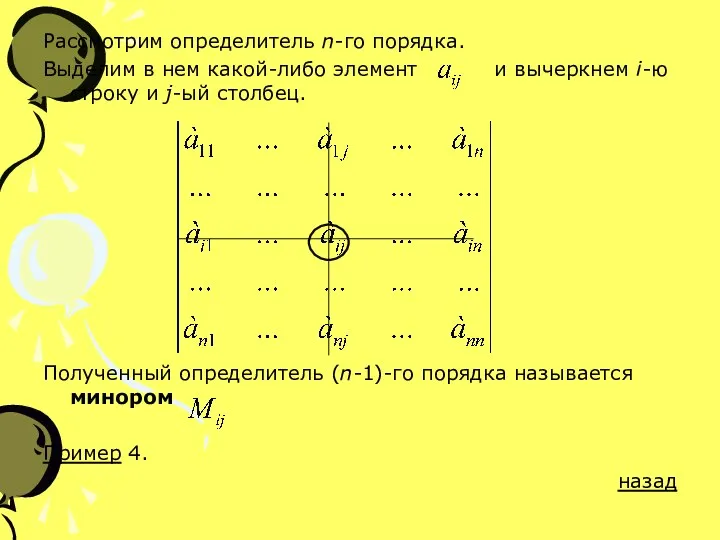
Рассмотрим определитель n-го порядка.
Выделим в нем какой-либо элемент и вычеркнем i-ю

Пример 4.
Вычислить миноры для всех элементов матриц:
2)
Ответ
назад

Ответ (Пример 4):
1)
2)
назад

Алгебраическим дополнением элемента называется число
Пример 5. Найти алгебраические дополнения для

Ответ (Пример 5):
1)
2)
назад

Вычисление определителя n-го порядка
Теорема Лапласа. Выберем в определителе n-го порядка

Пример 6. Вычислить определитель матрицы с помощью теоремы Лапласа
Решение:
1) Выберем произвольное

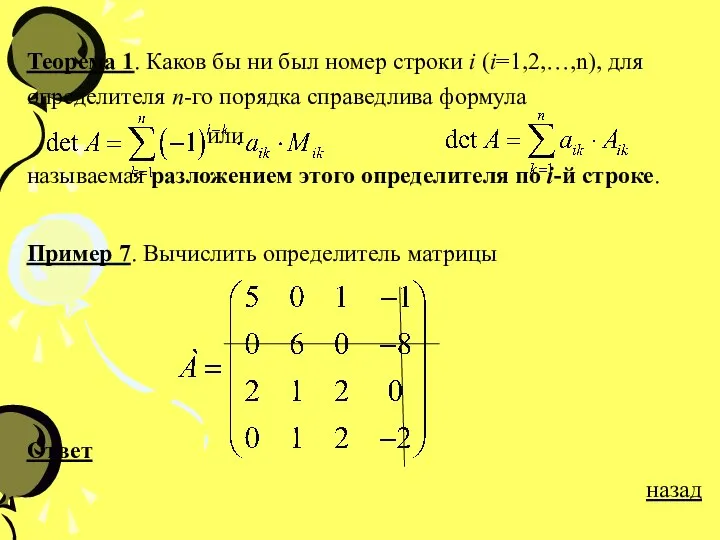
Теорема 1. Каков бы ни был номер строки i (i=1,2,…,n), для

Решение (Пример 7):
1) Выберем произвольную строку, например, 2-ю строку.
2) Воспользуемся теоремой

Теорема 2. Каков бы ни был номер столбца k (k=1,2,…,n), для

Свойства определителей:
Определитель не изменится при замене всех его строк соответствующими

Пример 1):
Проверить , если
назад

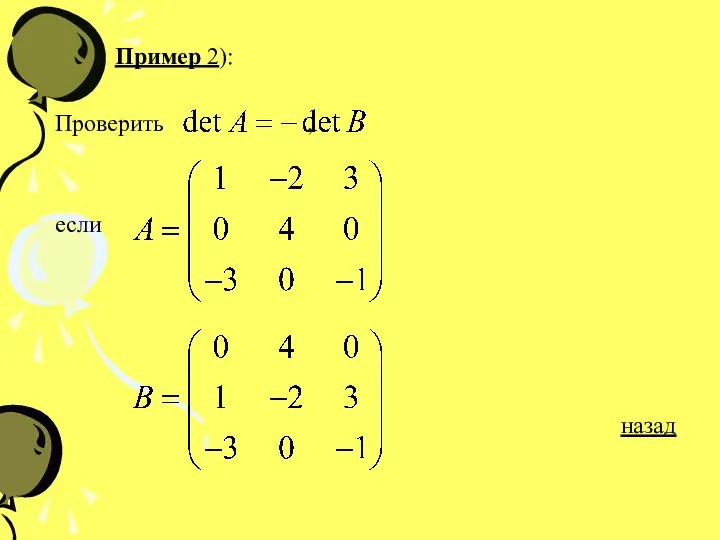
Пример 2):
Проверить ,
если
назад

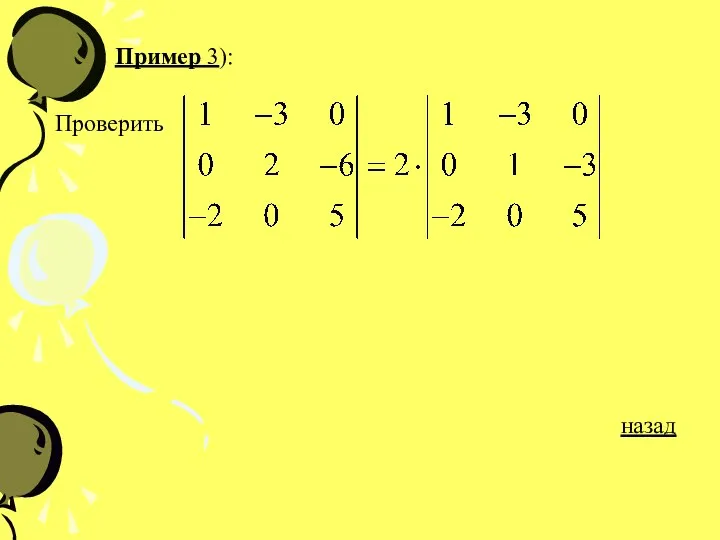
Пример 3):
Проверить
назад

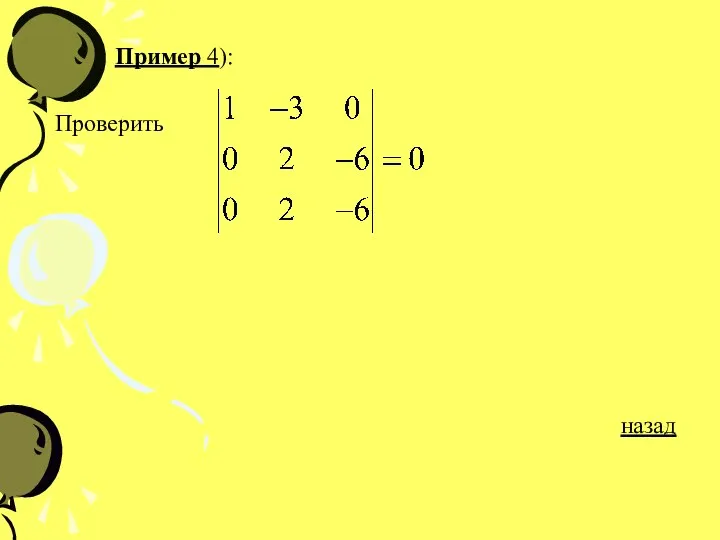
Пример 4):
Проверить
назад

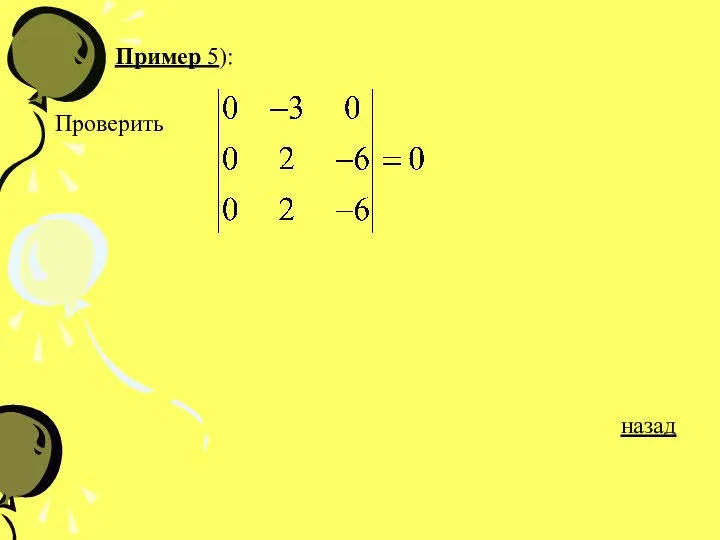
Пример 5):
Проверить
назад

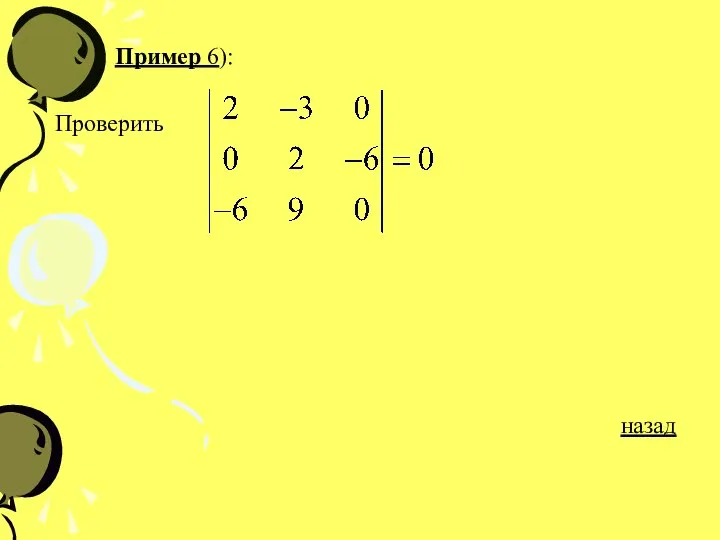
Пример 6):
Проверить
назад

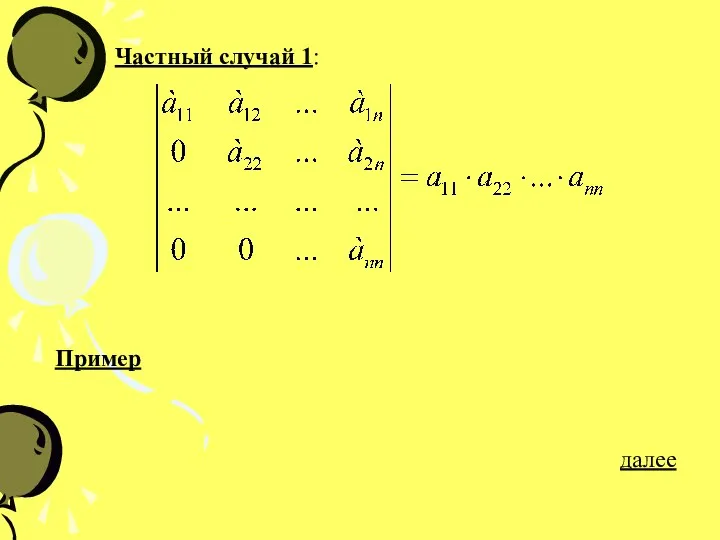
Частный случай 1:
Пример
далее

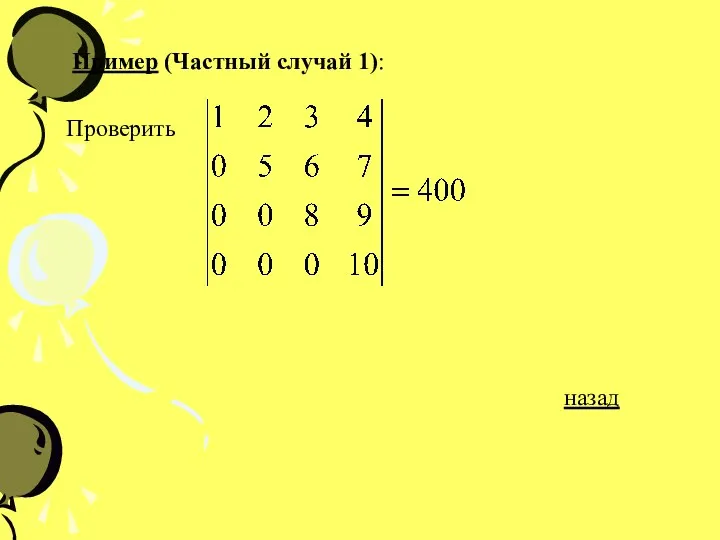
Пример (Частный случай 1):
Проверить
назад

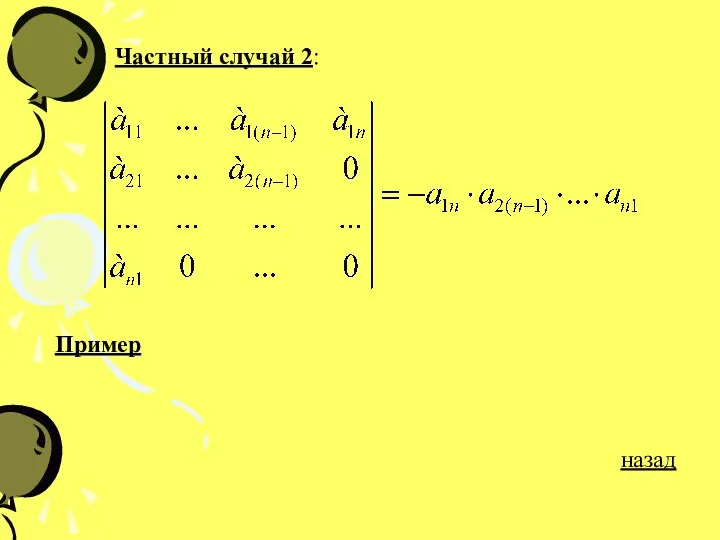
Частный случай 2:
Пример
назад