Содержание
- 2. 3.1. δ – функция Дирака В 1930 году для решения задач теоретической физики английскому физику П.
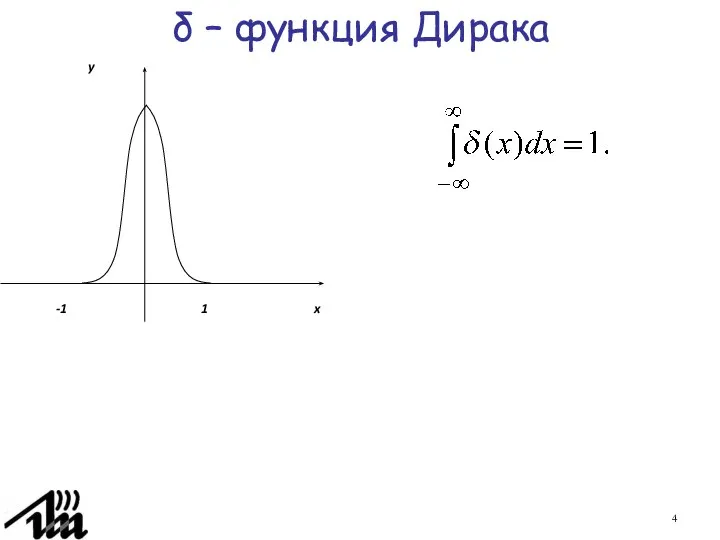
- 3. δ – функция Дирака П. Дирак определил дельта-функцию δ(x) следующим образом: Кроме того задается условие:
- 4. δ – функция Дирака
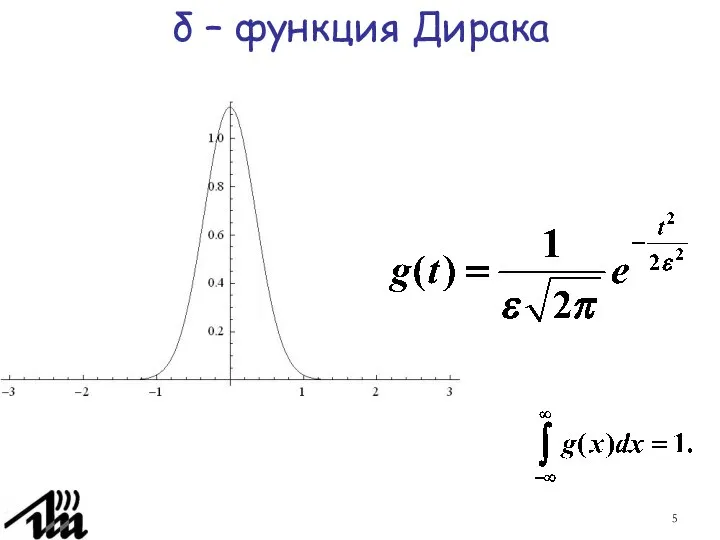
- 5. δ – функция Дирака
- 6. кафедра ЮНЕСКО по НИТ δ – функция Дирака Чем более узкой сделать полоску между левой и
- 7. кафедра ЮНЕСКО по НИТ δ – функция Дирака δ(x) не является функцией в обычном смысле, так
- 8. кафедра ЮНЕСКО по НИТ δ – функция Дирака Функции, из которых предельным переходом получается δ –
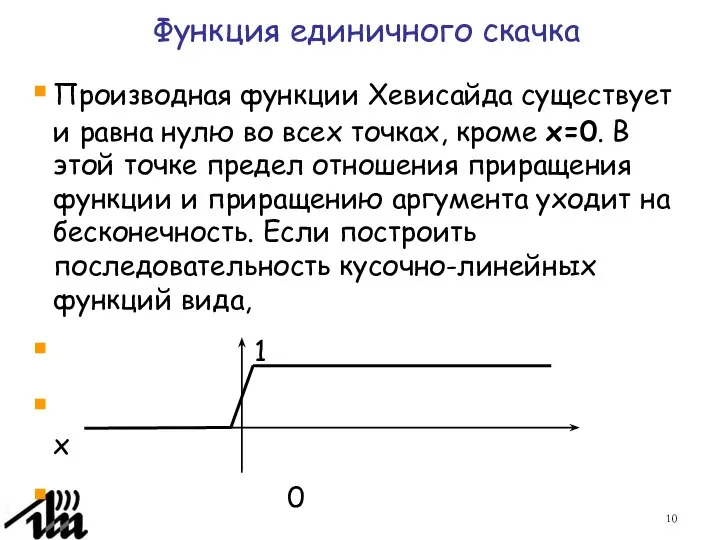
- 9. Функция единичного скачка Определим функцию единичного скачка, которая называется еще функцией Хевисайда: Ee график 1 x
- 10. Производная функции Хевисайда существует и равна нулю во всех точках, кроме x=0. В этой точке предел
- 11. то очевидно, что производными для таких функций служат ступенчатые функции (прямоугольные импульсы !), последовательность которых стремится
- 12. 3.2. Функция распределения дискретной случайной величины Пусть дискретная случайная величина X(ω) принимает три значения x1 =
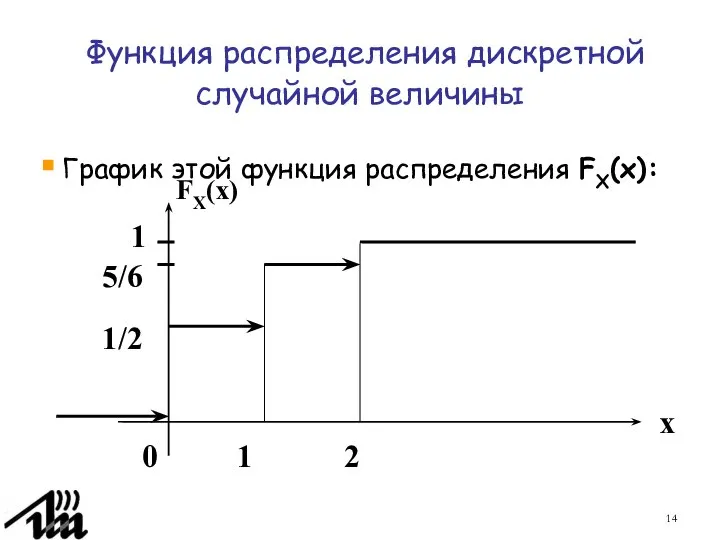
- 13. Функция распределения дискретной случайной величины Тогда функция распределения FX(x) дискретной случайной величины X(ω) по определению равна
- 14. Функция распределения дискретной случайной величины График этой функция распределения FX(x): 1/2 5/6 FX(x) 1 0 2
- 15. Функция распределения дискретной случайной величины Как известно из теории вероятностей, производной такой функция распределения FX(x) не
- 16. кафедра ЮНЕСКО по НИТ Функция распределения дискретной случайной величины Для построения функции плотности pX(x) вначале построим
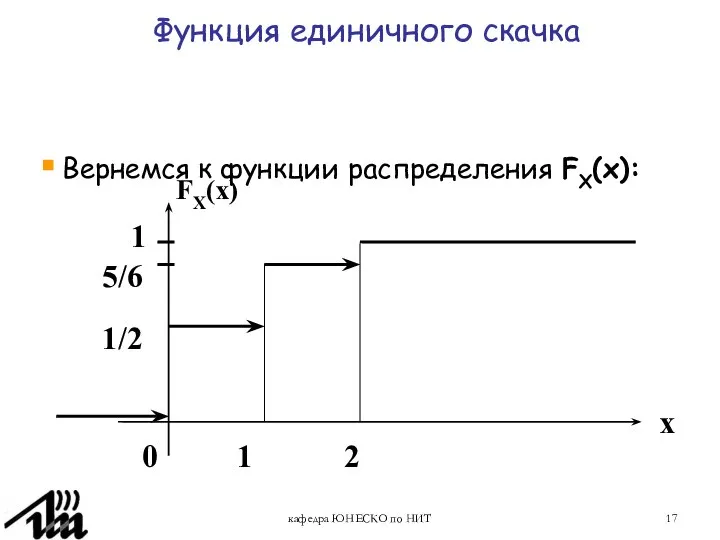
- 17. кафедра ЮНЕСКО по НИТ Вернемся к функции распределения FX(x): 1/2 5/6 FX(x) 1 0 2 x
- 18. Функция распределения дискретной случайной величины Такую функцию плотности FX(x) можно выразить через функцию единичного скачка 1(x)
- 19. Функция распределения дискретной случайной величины Функцию плотности FX(x) можно записать через функцию единичного скачка 1(x) в
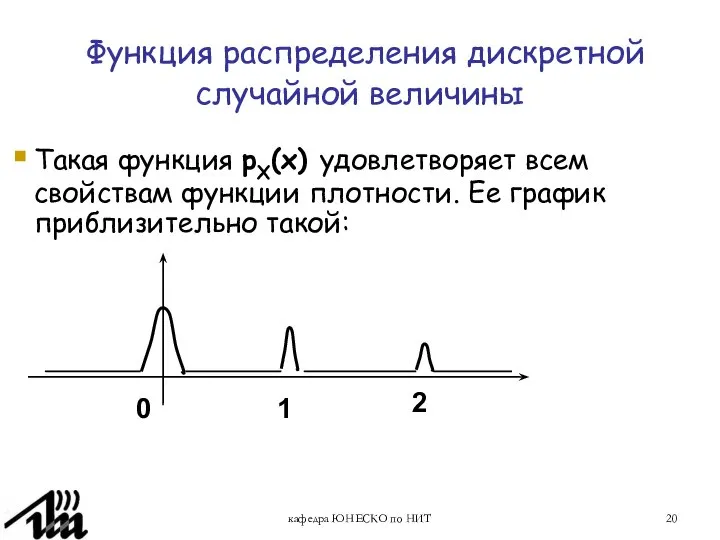
- 20. кафедра ЮНЕСКО по НИТ Функция распределения дискретной случайной величины Такая функция pX(x) удовлетворяет всем свойствам функции
- 21. кафедра ЮНЕСКО по НИТ 3.2. Преобразование Лапласа Преобразование Лапласа применяется для исследования дифференциальных уравнений. Оно преобразует
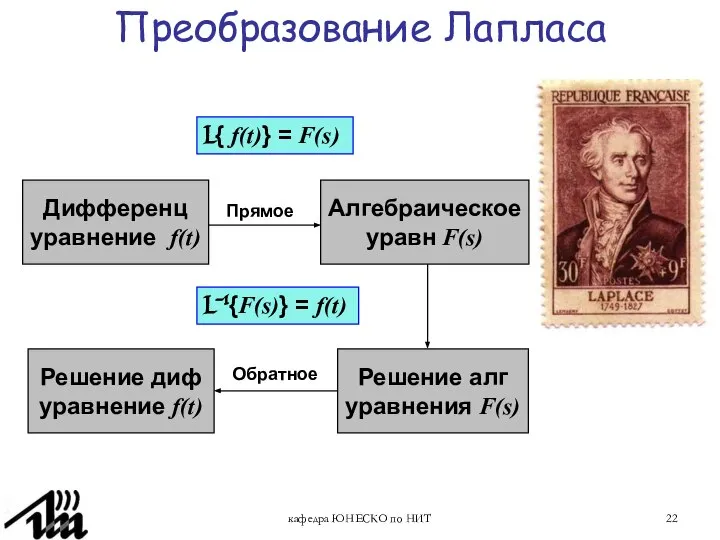
- 22. кафедра ЮНЕСКО по НИТ Преобразование Лапласа L{ f(t)} = F(s) Дифференц уравнение f(t) Алгебраическое уравн F(s)
- 23. кафедра ЮНЕСКО по НИТ Преобразование Лапласа Преобразованием Лапласа F(s) функции f(t), определенной для t ≥ 0,
- 24. кафедра ЮНЕСКО по НИТ Преобразование Лапласа Пример. Найти преобразование Лапласа функции единичного скачка (Хевисайда) Решение. При
- 25. кафедра ЮНЕСКО по НИТ Преобразование Лапласа Пример. Найти преобразование Лапласа функции eat Решение. При Re (a-s)
- 26. кафедра ЮНЕСКО по НИТ Преобразование Лапласа Функция Хевисайда от аргумента (x-a) - важная ступенчатая функция, найдем
- 27. кафедра ЮНЕСКО по НИТ Преобразование Лапласа Найдем преобразование Лапласа для функции Хевисайда с параметром a>0. Если
- 28. кафедра ЮНЕСКО по НИТ Преобразование Лапласа Существуют таблицы преобразований Лапласа f(t) F(s) _ _ _ _
- 29. кафедра ЮНЕСКО по НИТ Преобразование Лапласа Свойства преобразования Лапласа 1. Линейность: L(a·f(t) + b·g(t)) = a·L(f(t))
- 30. кафедра ЮНЕСКО по НИТ Преобразование Лапласа Применяя свойство 3 найдем преобразование Лапласа для дельта-функции δ(t -
- 31. кафедра ЮНЕСКО по НИТ Преобразование Лапласа Пример. Применение преобразования Лапласа к диф уравнению RC-цепи. x(t) =
- 32. кафедра ЮНЕСКО по НИТ Преобразование Лапласа Пример. Применение преобразования Лапласа к диф уравнению RC-цепи. Если задана
- 33. кафедра ЮНЕСКО по НИТ Преобразование Лапласа Пример. Применение преобразования Лапласа к диф уравнению колебания. y′′(t) +
- 34. кафедра ЮНЕСКО по НИТ 3.3. Обратное преобразование Лапласа Преобразования Лапласа содержит интеграл с пределами интегрирования от
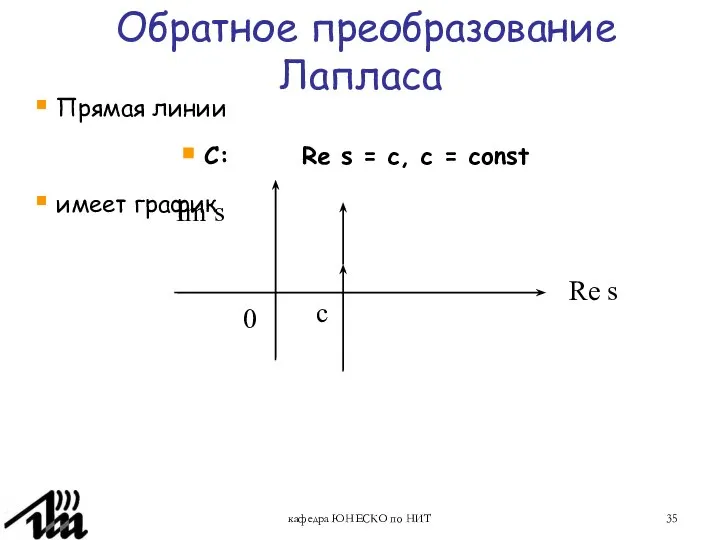
- 35. кафедра ЮНЕСКО по НИТ Обратное преобразование Лапласа Прямая линии C: Re s = c, c =
- 36. кафедра ЮНЕСКО по НИТ Обратное преобразование Лапласа Вспоминаем высшую математику Интегрирование функции от двух переменных по
- 37. кафедра ЮНЕСКО по НИТ Обратное преобразование Лапласа Вспоминаем высшую математику Если контур замкнут и функция f(x,y)
- 38. кафедра ЮНЕСКО по НИТ Обратное преобразование Лапласа Вспоминаем высшую математику Если при этом функция f(x,y) от
- 39. кафедра ЮНЕСКО по НИТ Обратное преобразование Лапласа Вспоминаем высшую математику Если , то вычет в точке
- 40. кафедра ЮНЕСКО по НИТ Обратное преобразование Лапласа Пример. Найти обратное преобразование Лапласа функции Требуется вычислить интеграл
- 41. кафедра ЮНЕСКО по НИТ Обратное преобразование Лапласа Пример. Найти обратное преобразование для F(s) Функцию дробно-рационального вида
- 42. кафедра ЮНЕСКО по НИТ Обратное преобразование Лапласа Пример. Найти обратное преобразование для F(s) Тогда Лаплас прообраз
- 43. Page Обратное преобразование Лапласа Преобразование Лапласа от свертки Доказательство:
- 45. Скачать презентацию


































 Жаһандану ұғымы
Жаһандану ұғымы Вертолет Ми-8МТВ. Система отопления и вентиляции
Вертолет Ми-8МТВ. Система отопления и вентиляции Презентация Крахмал
Презентация Крахмал Введение в CSS
Введение в CSS Понятие технического канала утечки информации. Понятие акустического канала утечки информации
Понятие технического канала утечки информации. Понятие акустического канала утечки информации Das kann ich. 6 урок
Das kann ich. 6 урок Основные понятия о взаимозаменяемости и точности в машиностроении
Основные понятия о взаимозаменяемости и точности в машиностроении Ojciec Święty Jan Paweł II
Ojciec Święty Jan Paweł II Православный храм
Православный храм Фредери́к Франсуа́ Шопе́н 1810 - 1849
Фредери́к Франсуа́ Шопе́н 1810 - 1849  Этнографический музей народов Байкала
Этнографический музей народов Байкала Русская трапеза - презентация для начальной школы_
Русская трапеза - презентация для начальной школы_ Weihnachten in Deutschland
Weihnachten in Deutschland Жизненные цели подростков
Жизненные цели подростков Призначення, склад та технічні характеристики телефонних апаратів систем МБ, ЦБ. Класифікація АТС
Призначення, склад та технічні характеристики телефонних апаратів систем МБ, ЦБ. Класифікація АТС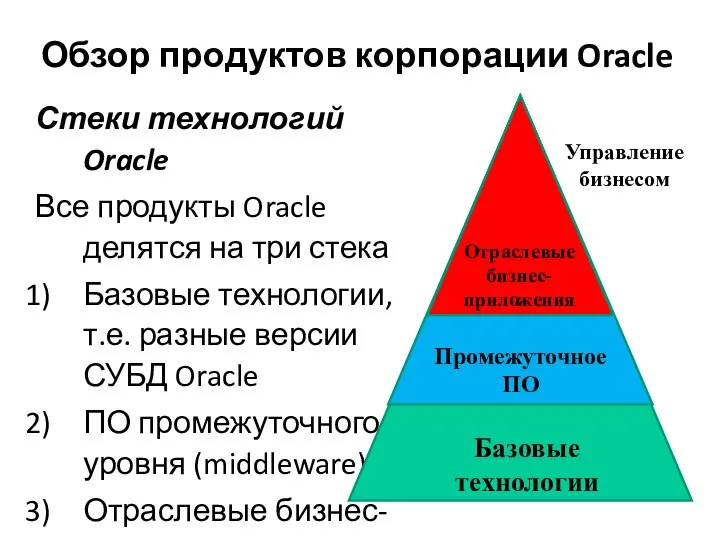 Продукты Oracle
Продукты Oracle  Т р у х а н о в отдых & развлечения банкет-холл
Т р у х а н о в отдых & развлечения банкет-холл ВЕЛИКАЯ ВОЙНА И ВЕЛИКАЯ ПОБЕДА г. Нижний Новгород учитель начальных классов Резаева Т.М.
ВЕЛИКАЯ ВОЙНА И ВЕЛИКАЯ ПОБЕДА г. Нижний Новгород учитель начальных классов Резаева Т.М.  Защита фидеров тяговой подстанции и постов секционирования двухпутного участка переменного тока с узловой схемой питания
Защита фидеров тяговой подстанции и постов секционирования двухпутного участка переменного тока с узловой схемой питания Общая характеристика Судебника 1550 г. Выполнила студентка Группы Ю-104 Чуева Яна
Общая характеристика Судебника 1550 г. Выполнила студентка Группы Ю-104 Чуева Яна Характеристики интегральных схем (ИС)
Характеристики интегральных схем (ИС) Организация деятельности архива медицинской организации
Организация деятельности архива медицинской организации Best fiesta: Christmas
Best fiesta: Christmas Общая характеристика изменений морфологического строя русского языка
Общая характеристика изменений морфологического строя русского языка Юзабилити. Тестирование
Юзабилити. Тестирование Синхронные машины
Синхронные машины Асбестоцементные материалы и асбестоцемент
Асбестоцементные материалы и асбестоцемент Ежегодная межвузовская студенческая научно-практическая конференция «Политическая конфликтология: теория и практика»
Ежегодная межвузовская студенческая научно-практическая конференция «Политическая конфликтология: теория и практика»