Содержание
- 2. Основной математический аппарат 3.1. δ – функция Дирака. 3.2. Функция единичного скачка. 3.3. Функция распределения дискретной
- 3. 3.1. δ – функция Дирака В 1930 году для решения задач теоретической физики английскому физику П.
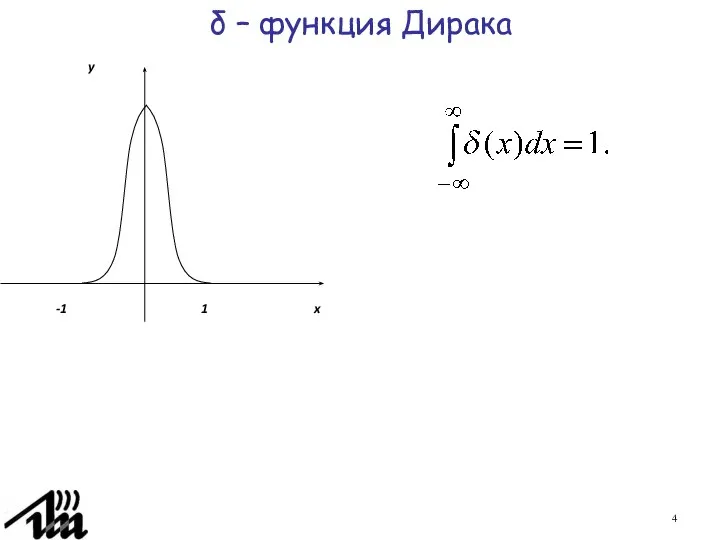
- 4. δ – функция Дирака
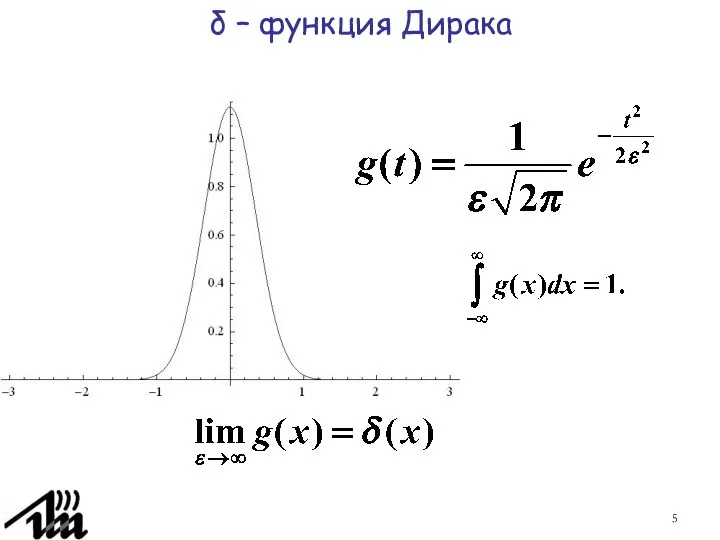
- 5. δ – функция Дирака
- 6. δ – функция Дирака Чем более узкой сделать полоску между левой и правой ветвью, тем выше
- 7. δ – функция Дирака Функции, из которых предельным переходом получается δ – функция могут быть непрерывными
- 8. 3.2. Функция единичного скачка Определим функцию единичного скачка, которая называется еще функцией Хевисайда: Ee график 1
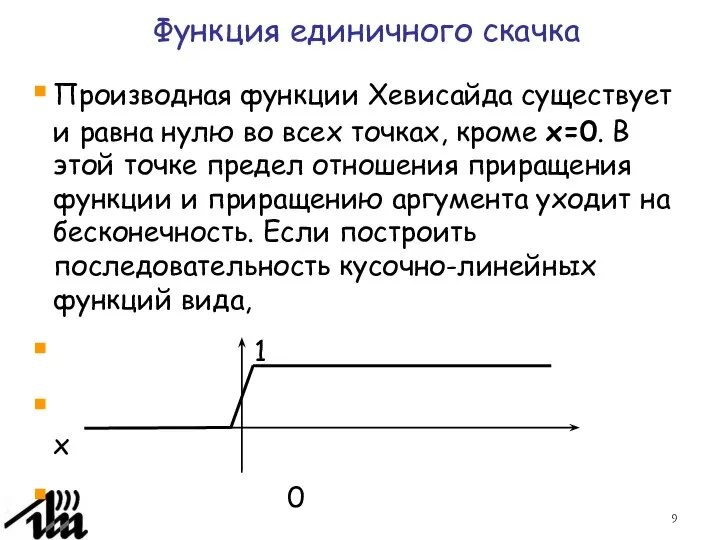
- 9. Производная функции Хевисайда существует и равна нулю во всех точках, кроме x=0. В этой точке предел
- 10. То функции такого вида выражаются в виде Функция единичного скачка x A (x = 0, y
- 11. Производные таких функций равны Функция единичного скачка При а = 1, 2, … получается последовательность производных,
- 12. 3.3. Функция распределения дискретной случайной величины Пусть дискретная случайная величина X(ω) принимает три значения x1 =
- 13. Функция распределения дискретной с.в. Тогда функция распределения FX(x) дискретной случайной величины X(ω) по определению равна FX(x)
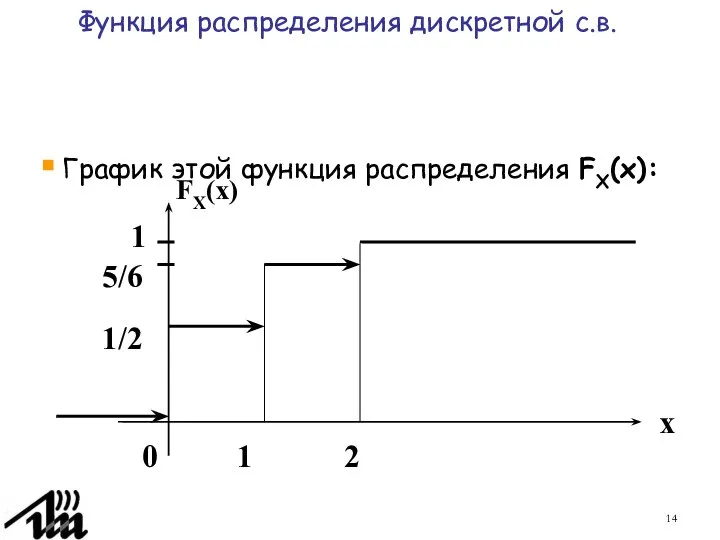
- 14. График этой функция распределения FX(x): Функция распределения дискретной с.в. 1/2 5/6 FX(x) 1 0 2 x
- 15. Как известно из теории вероятностей, производной такой функция распределения FX(x) не существует, то есть случайная величина
- 16. кафедра ЮНЕСКО по НИТ Для построения функции плотности pX(x) вначале построим функцию распределения FX(x) с использованием
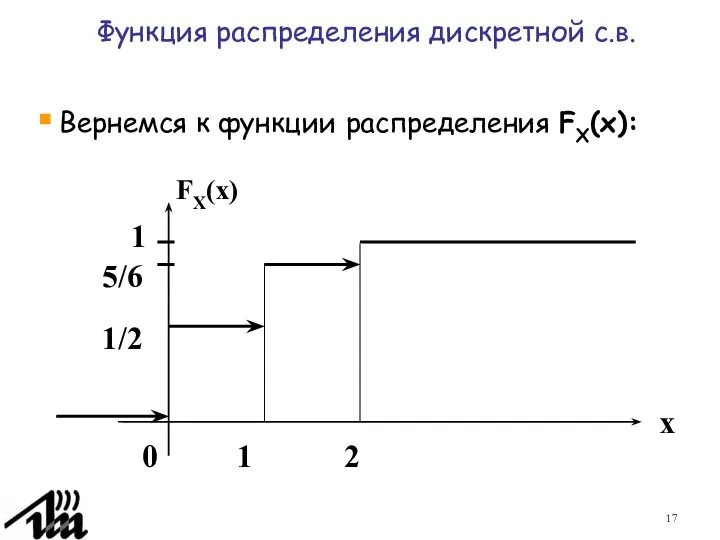
- 17. Вернемся к функции распределения FX(x): 1/2 5/6 FX(x) 1 0 2 x 1 Функция распределения дискретной
- 18. Такую функцию плотности FX(x) можно выразить через функцию единичного скачка 1(x) . В точках разрыва функция
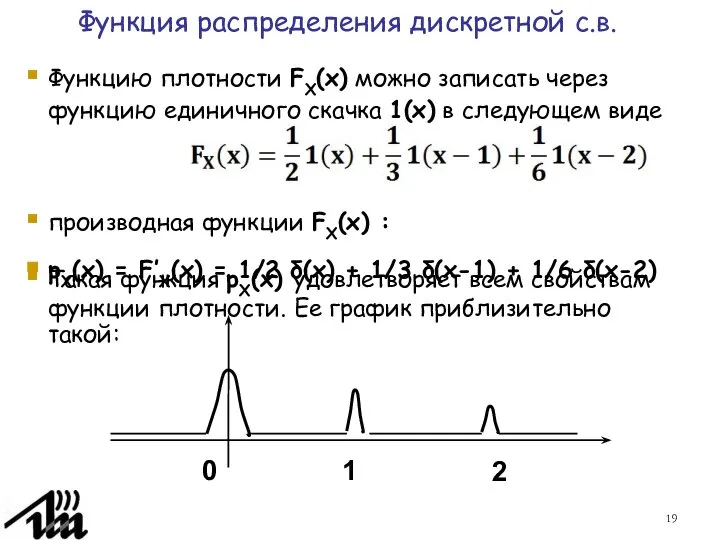
- 19. Функцию плотности FX(x) можно записать через функцию единичного скачка 1(x) в следующем виде производная функции FX(x)
- 20. 3.4. Преобразование Лапласа Преобразование Лапласа применяется для исследования дифференциальных уравнений. Оно преобразует дифференциальное уравнение в алгебраическое,
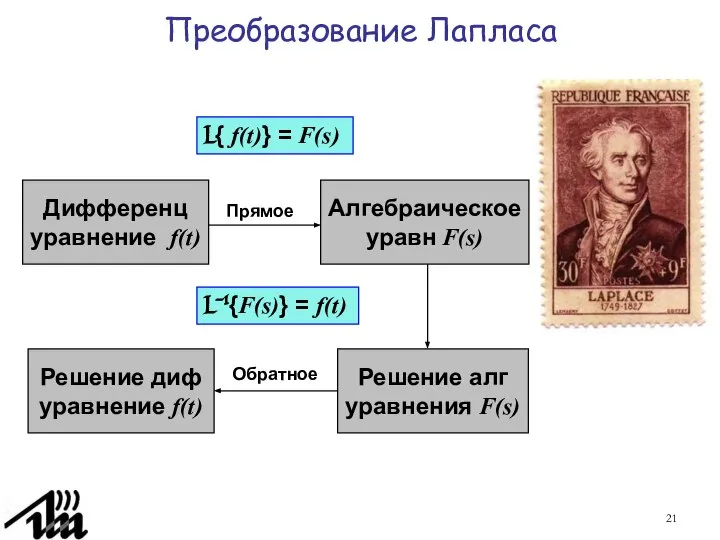
- 21. Преобразование Лапласа L{ f(t)} = F(s) Дифференц уравнение f(t) Алгебраическое уравн F(s) Решение алг уравнения F(s)
- 22. Преобразование Лапласа Преобразованием Лапласа F(s) функции f(t), определенной для t ≥ 0, называется интегральное преобразование: (для
- 23. Преобразование Лапласа Пример. Найти преобразование Лапласа функции единичного скачка (Хевисайда) Решение. При Re s > 0
- 24. Преобразование Лапласа Пример. Найти преобразование Лапласа функции eat Решение. При Re (a-s)
- 25. Преобразование Лапласа Найдем преобразование Лапласа для функции Хевисайда 1(x-a) с параметром a>0. Если Re s >
- 26. Преобразование Лапласа Найдем преобразование Лапласа для функций sin ωt и cos ωt с параметром ω≠0. Интегрирование
- 27. Преобразование Лапласа Переходит к определенному интегралу :
- 28. Преобразование Лапласа Упражнение. Найти преобразование Лапласа для функций f(t) = t, f(t) = t2.
- 29. Преобразование Лапласа Существуют таблицы преобразований Лапласа
- 30. Преобразование Лапласа Свойства преобразования Лапласа 1. Линейность: L(a·f(t) + b·g(t)) = a·L(f(t)) + b·L(g(t)). 2. Свойство
- 31. Преобразование Лапласа
- 32. Доказательство интегрального свойства (свойство 4) Преобразование Лапласа Тогда Определим функцию g(t) :
- 33. (иначе интеграл расходится и преобразования Лапласа не существует) поэтому Преобразование Лапласа Значение нижней подстановки равно 0,
- 34. Преобразование Лапласа Применяя свойство 3 найдем преобразование Лапласа для дельта-функции δ(t - a), (а>0). Эта функция
- 35. 3.5.Решение диф. уравнений преобразованием Лапласа Применение преобразования Лапласа к диф уравнению RC-цепи. x(t) = С*R *
- 36. Если задана функция x(t), то это выражение дает решение исходного дифференциального уравнения (но это Лаплас–образ решения!).
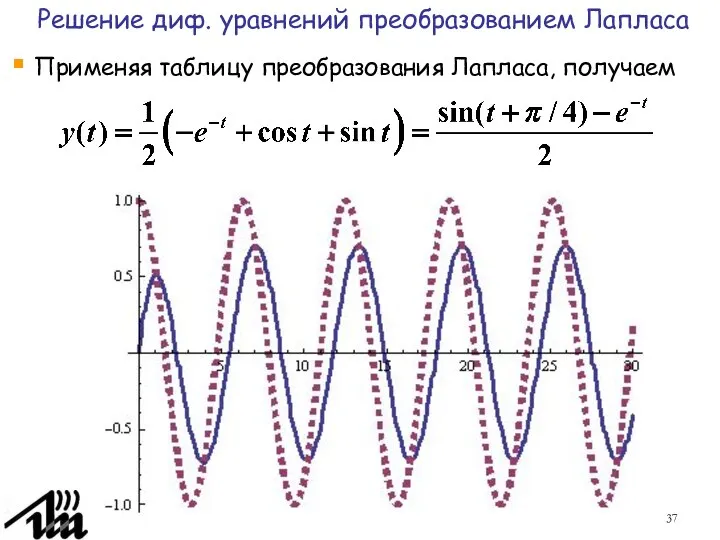
- 37. Применяя таблицу преобразования Лапласа, получаем Решение диф. уравнений преобразованием Лапласа
- 38. Пример. Применение преобразования Лапласа к дифференциальному уравнению колебания : y′′(t) + ω2y(t) = r(t) Дважды применяя
- 39. Пусть ω =1, y(0) = y’(0)=1, r(t) = sin 2t. Тогда Решение диф. уравнений преобразованием Лапласа
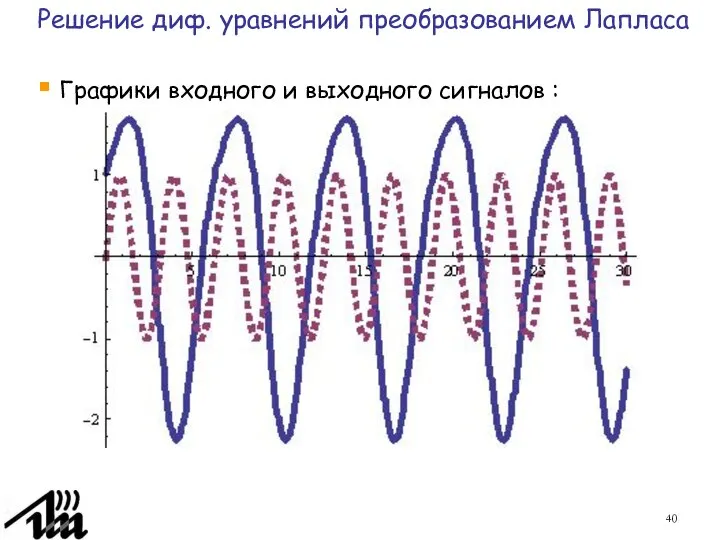
- 40. Графики входного и выходного сигналов : Решение диф. уравнений преобразованием Лапласа
- 41. 3.6. Обратное преобразование Лапласа Преобразования Лапласа содержит интеграл с пределами интегрирования от 0 до +∞. Будем
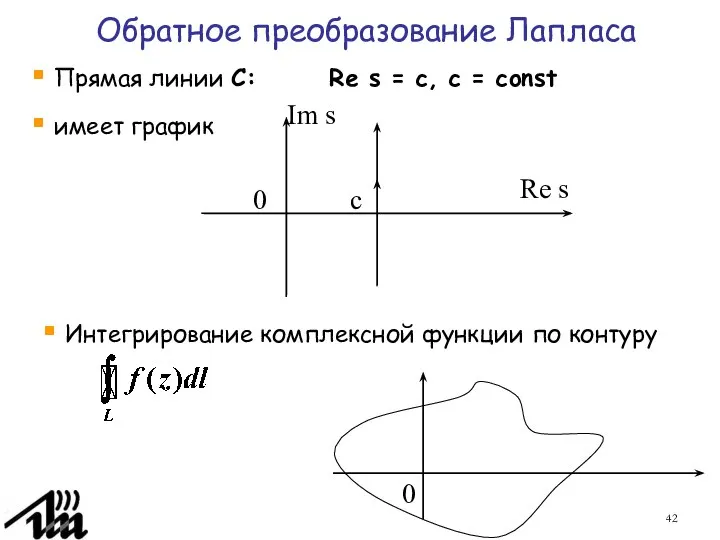
- 42. Обратное преобразование Лапласа Прямая линии C: Re s = c, c = const имеет график 0
- 43. Обратное преобразование Лапласа Вспоминаем высшую математику 1) Если контур замкнут и комплексная функция f(z), z=x+iy имеет
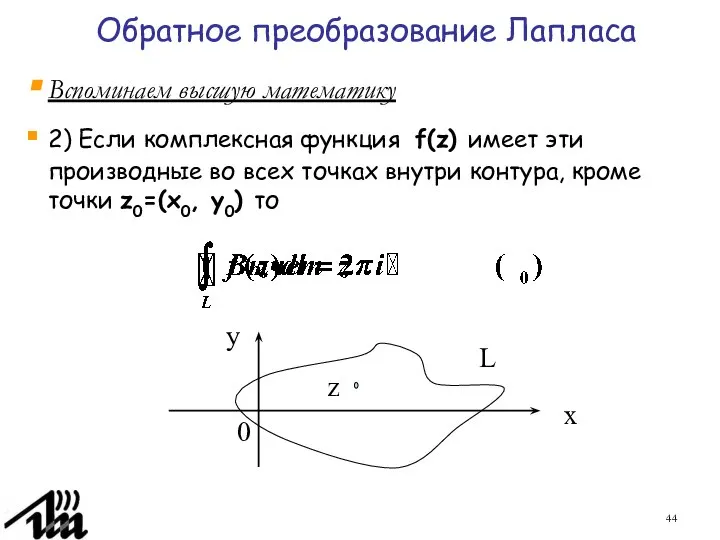
- 44. Обратное преобразование Лапласа Вспоминаем высшую математику 2) Если комплексная функция f(z) имеет эти производные во всех
- 45. Обратное преобразование Лапласа Вспоминаем высшую математику Если , g(z) – аналитическая функция, то вычет в точке
- 46. Обратное преобразование Лапласа Пример. Найти интеграл по контуру от комплексной функции Заменяем переменную s на α
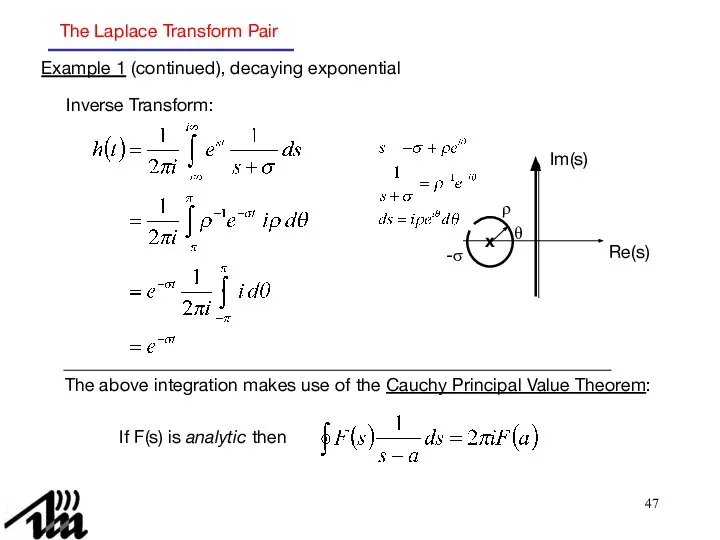
- 47. The Laplace Transform Pair Inverse Transform: The above integration makes use of the Cauchy Principal Value
- 48. Обратное преобразование Лапласа Существуют 2 способа вычисления обратного преобразования Лапласа : 1) вычислять интеграл на прямой
- 49. Обратное преобразование Лапласа
- 50. Обратное преобразование Лапласа Обратное преобразование Лапласа от рациональной функции. Функция F(s) называется рациональной, если где N(s)
- 51. Обратное преобразование Лапласа Пример. Найти обратное преобразование Лапласа функции Требуется вычислить интеграл 0 с Re s
- 52. Обратное преобразование Лапласа Рациональную функцию F(s) интегрируют простыми правилами. 1) F(s) разлагается в сумму простых дробей,
- 53. Page Обратное преобразование Лапласа Преобразование Лапласа от свертки Доказательство:
- 54. Page Обратное преобразование Лапласа В частности, для свертки с импульсом получается: Обратное преобразование от произведения функций
- 55. Page Обратное преобразование Лапласа Покажем, что :
- 56. 3.7.z-преобразование Цифровая обработка сигналов есть не что иное, как обработка последовательностей (дискретных значений сигнала). Для обработки
- 58. Скачать презентацию











































 Проект механічної дільниці на базі багатошпиндельних верстатів з виготовлення деталі "колесо зубчасте"
Проект механічної дільниці на базі багатошпиндельних верстатів з виготовлення деталі "колесо зубчасте" Показатели качества воды и их определение
Показатели качества воды и их определение М. Портер и его роль в развитии теории конкурентоспособности Подготовил: Безнощук Богдан, студент 4 курса, ДС-01
М. Портер и его роль в развитии теории конкурентоспособности Подготовил: Безнощук Богдан, студент 4 курса, ДС-01 Игра с рисками Михаил Гедзберг Luxoft MGedzberg@luxoft.com
Игра с рисками Михаил Гедзберг Luxoft MGedzberg@luxoft.com Романтизм в сценическом костюме XIX века
Романтизм в сценическом костюме XIX века Презентация на тему "Ретровирусы" - скачать презентации по Медицине
Презентация на тему "Ретровирусы" - скачать презентации по Медицине Розробка бібліотеки для динамічного завантаження виконуваного коду в запущений процес
Розробка бібліотеки для динамічного завантаження виконуваного коду в запущений процес Коммуникационное обеспечение международной логической инфраструктуры Выполнила студентка 4-го курса группа ДС-04 Улан кызы А
Коммуникационное обеспечение международной логической инфраструктуры Выполнила студентка 4-го курса группа ДС-04 Улан кызы А Переходные процессы в электроэнергетике
Переходные процессы в электроэнергетике Сферы жизнедеятельности общества
Сферы жизнедеятельности общества Достопримечальности Киева
Достопримечальности Киева Презентация "Всемирный день качества" - скачать презентации по Экономике
Презентация "Всемирный день качества" - скачать презентации по Экономике Системные платы
Системные платы Динамические характеристики линейных систем
Динамические характеристики линейных систем Про вдосконалення системи технічного обслуговування, експлуатації, поточного та капітального ремонтів тягового рухомого складу
Про вдосконалення системи технічного обслуговування, експлуатації, поточного та капітального ремонтів тягового рухомого складу Jahreszeiten
Jahreszeiten Дисциплина труда. Трудовой распорядок
Дисциплина труда. Трудовой распорядок Гендерный подход в сексуально- гигиеническом просвещении учащихся 5-11 классов. Педагог- психолог МАОУ гимназия г. Нытва Лат
Гендерный подход в сексуально- гигиеническом просвещении учащихся 5-11 классов. Педагог- психолог МАОУ гимназия г. Нытва Лат Вебинар «Негатив – не приговор» Работа с негативом в социальных сетях и на тематических форумах
Вебинар «Негатив – не приговор» Работа с негативом в социальных сетях и на тематических форумах Духовые народные инструменты
Духовые народные инструменты Психологические особенности старших подростков
Психологические особенности старших подростков Акустическая эмиссия
Акустическая эмиссия Обучение и инструктаж по охране труда (ГУМ)
Обучение и инструктаж по охране труда (ГУМ) Жиры по органической химии
Жиры по органической химии Правила оформления чертежей
Правила оформления чертежей Структурная организация ферментов
Структурная организация ферментов Михаил Зощенко
Михаил Зощенко Флотация
Флотация