Содержание
- 2. Поиск кратчайших путей в графе
- 3. Алгоритм Дейкстры
- 4. Алгоритм Дейкстры
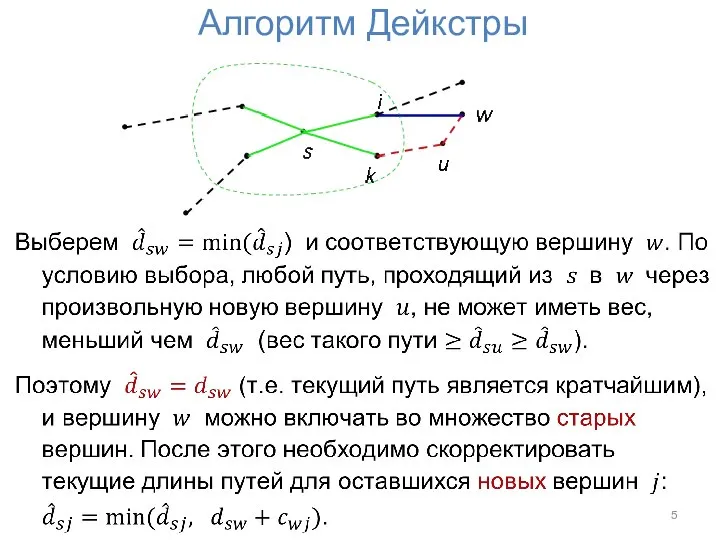
- 5. Алгоритм Дейкстры
- 6. Алгоритм Дейкстры
- 7. Алгоритм Дейкстры
- 8. Методы WGraph для алгоритма Дейкстры void WGraph::minpath(int s, double *D, int *P) { int i, j,
- 9. Выделение кратчайшего пути
- 10. Вычисление кратчайших расстояний от вершины s до всех остальных Матрица расстояний в общем случае несимметричная s=0
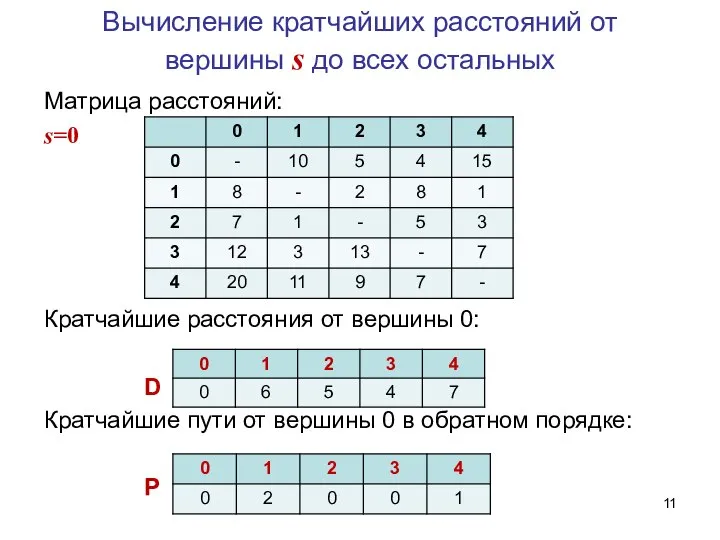
- 11. Вычисление кратчайших расстояний от вершины s до всех остальных Матрица расстояний: s=0 Кратчайшие расстояния от вершины
- 12. Алгоритм Флойда-Уоршалла
- 13. Алгоритм Флойда-Уоршалла
- 14. Алгоритм Флойда-Уоршалла
- 15. Алгоритм Флойда-Уоршалла Вычисляется матрица весов всех кратчайших путей. double** WGraph::allminpath() { int i, j, l; double
- 16. Замечания к алгоритму Флойда-Уоршалла Алгоритм Флойда-Уоршалла –пример использования динамического программирования. Условия, при которых применимо ДП: оптимизационная
- 17. Замечания к алгоритму Флойда-Уоршалла Порядок решения задачи с помощью ДП: описать структуру оптимальных решений задачи и
- 18. Эйлеровы циклы и пути Эйлеров цикл в неориентированном графе: начинается в произвольной вершине a проходит по
- 19. Идея алгоритма построения цикла/пути Вычисляются степени всех вершин. Если условия существования цикла/пути не выполняются, то выход.
- 20. Замечания по алгоритму Текущий путь и побочные циклы выгодно строить в виде списков. Используем для этого
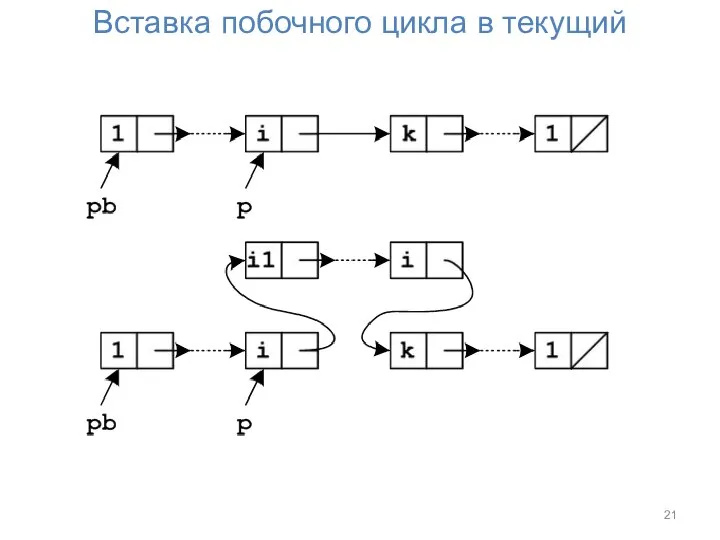
- 21. Вставка побочного цикла в текущий
- 22. Вставка списка в список Вставка списка sec после текущего элемента (текущая позиция pcurpos не изменяется): bool
- 23. Вспомогательные методы Проверка существования эйлерова цикла/пути и расчет начальной и конечной вершины (a и b, для
- 24. Вспомогательные методы Выделение произвольного пути из a в b (a=b в случае цикла) с исключением просмотренных
- 26. Скачать презентацию




















 Урок открытия нового знания - презентация для начальной школы_
Урок открытия нового знания - презентация для начальной школы_ Классификация страховых терминов
Классификация страховых терминов  Увлажнитель воздуха с ночником
Увлажнитель воздуха с ночником Классификатор бюджетных правонарушений и его применение органами государственного финансового контроля
Классификатор бюджетных правонарушений и его применение органами государственного финансового контроля Портреты эпохи Просвещения
Портреты эпохи Просвещения Алгоритмические языки программирования
Алгоритмические языки программирования Портрет на фоне малой Родины
Портрет на фоне малой Родины Деятельность саморегулируемых организаций по повышению качества работы кадастровых инженеров
Деятельность саморегулируемых организаций по повышению качества работы кадастровых инженеров Знакомство со Львовом
Знакомство со Львовом Правоохранительная деятельность, ее признаки, понятие и задачи. Органы, осуществляющие правоохранительную деятельность
Правоохранительная деятельность, ее признаки, понятие и задачи. Органы, осуществляющие правоохранительную деятельность Бином Ньютона. «Би»-удвоение, раздвоение … «Ном»(фран. nombre) –номер, нумерация. «Бином» -»два числа»
Бином Ньютона. «Би»-удвоение, раздвоение … «Ном»(фран. nombre) –номер, нумерация. «Бином» -»два числа» Подтягивание. Техники подтягивания
Подтягивание. Техники подтягивания Кухня в традициях коми
Кухня в традициях коми Современное пятиборье
Современное пятиборье European law
European law Инициативное предложение Никитина Н. А.
Инициативное предложение Никитина Н. А. Искусство XX века. Авангардизм
Искусство XX века. Авангардизм Управление процессом обучения на промышленном предприятии На материале ОАО «Каустик» Докладчик – начальник учебного центр
Управление процессом обучения на промышленном предприятии На материале ОАО «Каустик» Докладчик – начальник учебного центр Исследование прочностных характеристик сердечников крестовин стрелочных переводов после упрочняющей обработки
Исследование прочностных характеристик сердечников крестовин стрелочных переводов после упрочняющей обработки Духовні святині Охтирщини
Духовні святині Охтирщини Теория и история религии
Теория и история религии Общая физиология эндокринной системы
Общая физиология эндокринной системы Денежная реформа Елены Глинской
Денежная реформа Елены Глинской Кәмелетке толмағандар қылмыстылығының себептері және оның алдын алу мәселелері
Кәмелетке толмағандар қылмыстылығының себептері және оның алдын алу мәселелері Культура, традиции, праздники в Бразилии
Культура, традиции, праздники в Бразилии Сайт ГК. Контент. Рекламные блоки
Сайт ГК. Контент. Рекламные блоки Планирование питания туристов во время туристических походов и поездок
Планирование питания туристов во время туристических походов и поездок Машины постоянного тока
Машины постоянного тока