Содержание
- 2. Множества Множество —понятие не сводится к другим понятиям и не определяется Предметы (объекты), составляющие множество, называют
- 3. Операции над множествами Если каждый элемент множества A является элементом множества B, то говорят, что A
- 4. Операции над множествами Объединением двух множеств А и В называется множество, состоящее из всех элементов, принадлежащих
- 5. Операции над множествами Симметрической разностью множеств А и В называется множество, состоящее из всех элементов, принадлежащих
- 6. Свойства = U \ A= {х | х ∈ U, х ∉ A} А ∪ А
- 7. Формула включений и исключений «+», если количество множеств нечетное «–», если количество множеств четное. Чаще эту
- 8. Формула включений и исключений Обозначим через А — множество школьников, знающих английский язык; N — множество
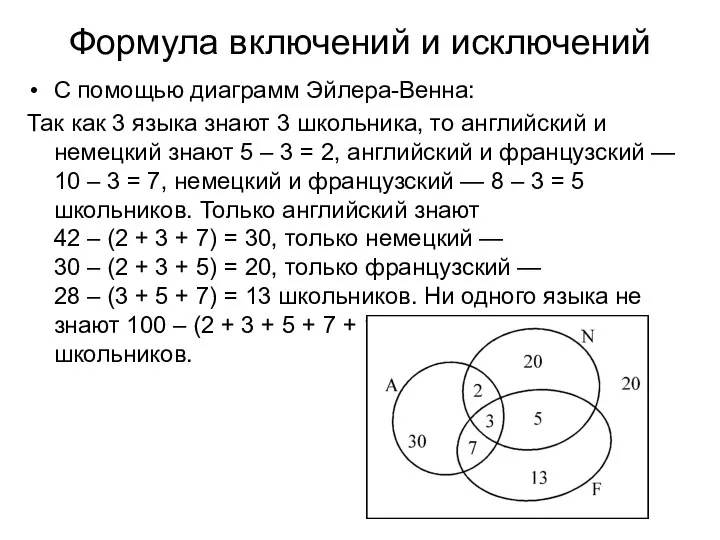
- 9. Формула включений и исключений С помощью диаграмм Эйлера-Венна: Так как 3 языка знают 3 школьника, то
- 10. Элементы комбинаторики Комбинаторика – это раздел математики, в котором исследуются и решаются задачи выбора элементов из
- 11. Правила комбинаторики Правило суммы: Если элемент можно выбрать способами, элемент - способами, …, - способами, то
- 13. Элементы комбинаторики Задача 2. В магазине есть 7 видов шариковых ручек и 5 видов гелиевых. Сколько
- 14. Упорядоченные выборки Если исходное множество состоит из n различных элементов, и при каждом выборе мы будем
- 15. Упорядоченные выборки Всякая упорядоченная выборка объема m из множества, состоящего из n различных объектов, называется размещением
- 16. Неупорядоченные выборки Всякая неупорядоченная выборка объема m из множества, состоящего из n различных объектов, называется сочетанием
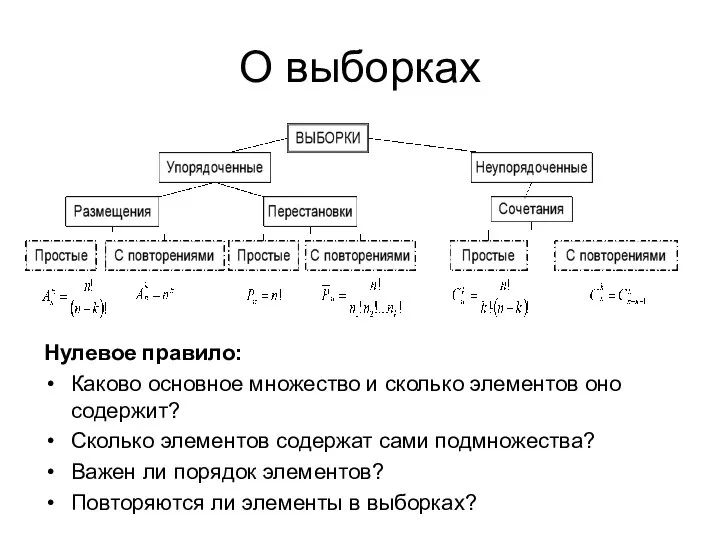
- 18. О выборках Нулевое правило: Каково основное множество и сколько элементов оно содержит? Сколько элементов содержат сами
- 19. Задачи Задача 6. Из 30 участников собрания надо выбрать председателя и секретаря. Сколькими способами это можно
- 21. Скачать презентацию
















 Принципи об’ємно-планувальних рішень в будівлях та спорудах
Принципи об’ємно-планувальних рішень в будівлях та спорудах Учебник продавца - кассира
Учебник продавца - кассира Puskin Kávéház - Moszkva
Puskin Kávéház - Moszkva Оценка качества
Оценка качества ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ЭЛЕКТРОТЕХНИКИ 5
ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ЭЛЕКТРОТЕХНИКИ 5 Российско-германское молодежное сотрудничество
Российско-германское молодежное сотрудничество День матери
День матери Miłość jak kwiat
Miłość jak kwiat Image Capture
Image Capture Формы организации физического воспитания в ДОУ
Формы организации физического воспитания в ДОУ Викторина по сказкам братьев Гримм - презентация для начальной школы_
Викторина по сказкам братьев Гримм - презентация для начальной школы_ Определение диаметра вала в опасном сечении из условия прочности на изгиб с кручением
Определение диаметра вала в опасном сечении из условия прочности на изгиб с кручением Болезнь Паркинсона Гитлера Выполнил: Айвазов И.Г 228 леч. Красноярск 2010
Болезнь Паркинсона Гитлера Выполнил: Айвазов И.Г 228 леч. Красноярск 2010  Особенности, регистры, подключение UART
Особенности, регистры, подключение UART Тема 1.PR в пространстве маркетинга
Тема 1.PR в пространстве маркетинга  Отчет о работе в 2018 году спортивной школы олимпийского резерва «Атлетика»
Отчет о работе в 2018 году спортивной школы олимпийского резерва «Атлетика» Опорные схемы и рисунки в помощь учащимся
Опорные схемы и рисунки в помощь учащимся Микросервисная архитектура
Микросервисная архитектура Rice Cooker HD3033 df Technical Info. Product Features
Rice Cooker HD3033 df Technical Info. Product Features Сланцевая революция. Мифы и реальность
Сланцевая революция. Мифы и реальность Культура детско-родительских отношений в роду
Культура детско-родительских отношений в роду Презентация Соборное уложение 1649г
Презентация Соборное уложение 1649г Внешняя политика Петра I
Внешняя политика Петра I Сергий Радонежский
Сергий Радонежский Глобальные проблемы человечества. Международный терроризм
Глобальные проблемы человечества. Международный терроризм Analysis of Statically Determinate Structures
Analysis of Statically Determinate Structures Красота в понимании древних греков
Красота в понимании древних греков Базовые понятия. Знакомство с C#
Базовые понятия. Знакомство с C#