Содержание
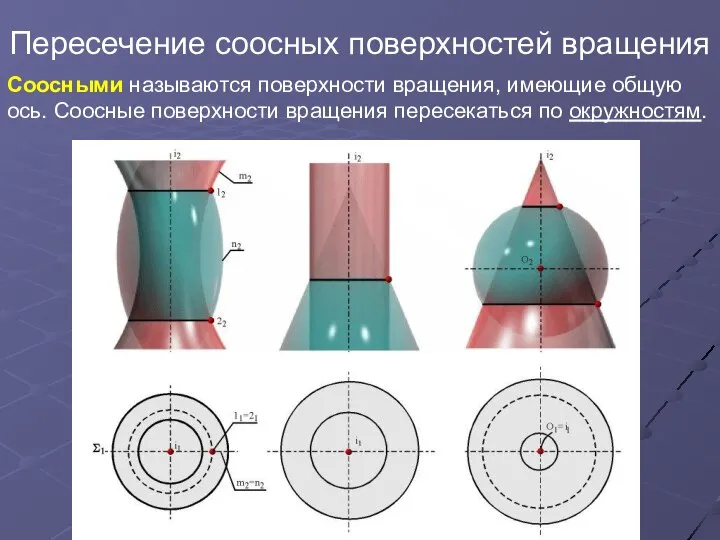
- 2. Пересечение соосных поверхностей вращения Соосными называются поверхности вращения, имеющие общую ось. Соосные поверхности вращения пересекаться по
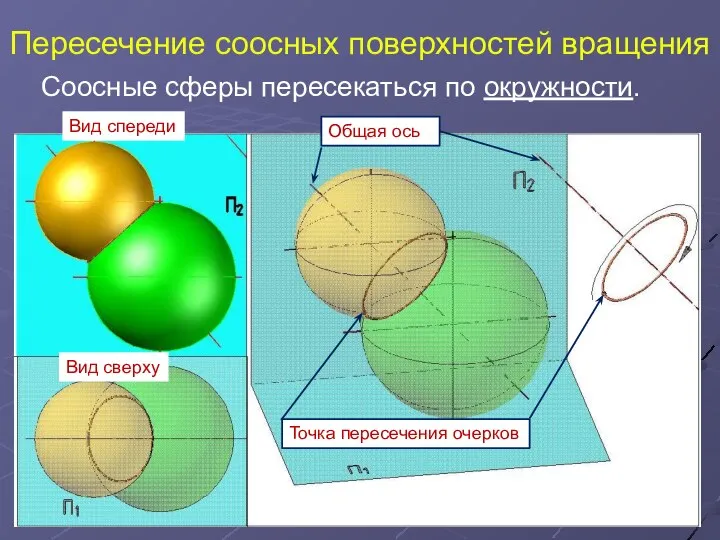
- 3. Пересечение соосных поверхностей вращения Соосные сферы пересекаться по окружности. Вид спереди Вид сверху Точка пересечения очерков
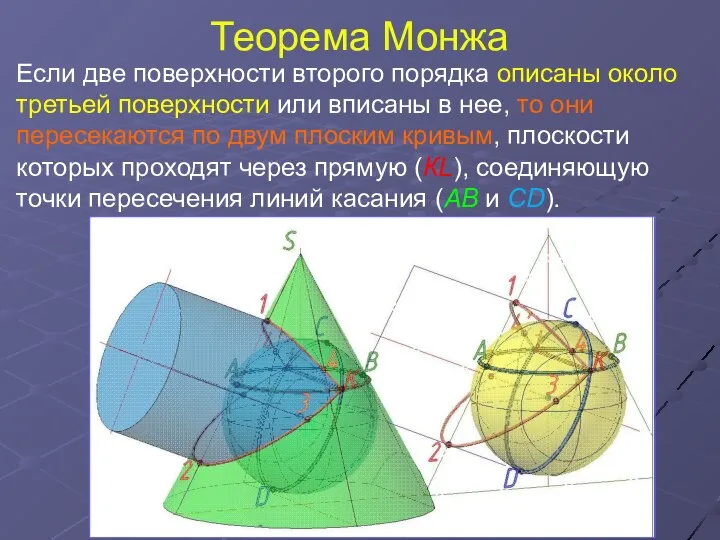
- 4. Теорема Монжа Если две поверхности второго порядка описаны около третьей поверхности или вписаны в нее, то
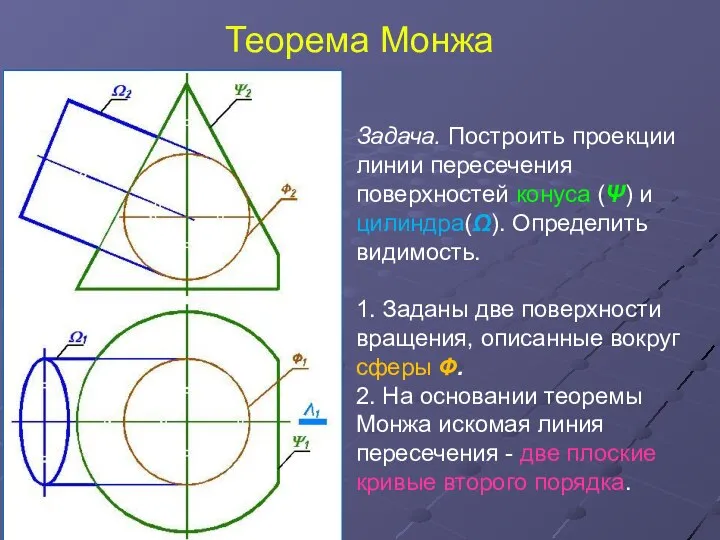
- 5. Теорема Монжа Задача. Построить проекции линии пересечения поверхностей конуса (Ψ) и цилиндра(Ω). Определить видимость. 1. Заданы
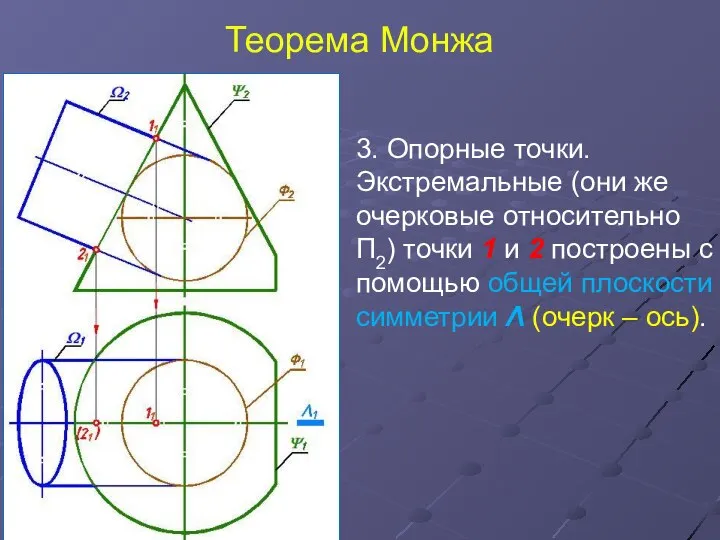
- 6. Теорема Монжа 3. Опорные точки. Экстремальные (они же очерковые относительно П2) точки 1 и 2 построены
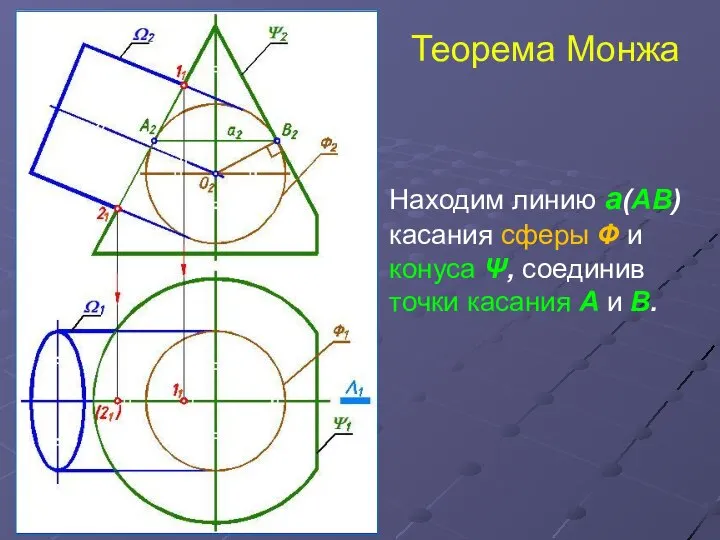
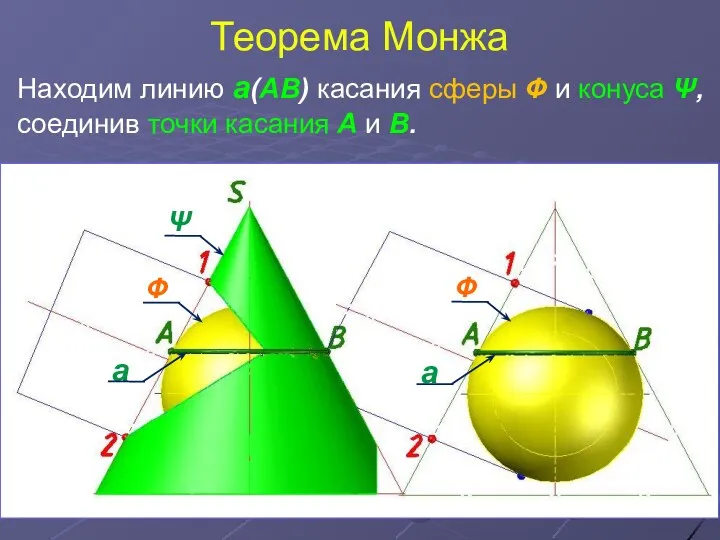
- 7. Теорема Монжа Находим линию а(АВ) касания сферы Ф и конуса Ψ, соединив точки касания А и
- 8. Теорема Монжа Находим линию а(АВ) касания сферы Ф и конуса Ψ, соединив точки касания А и
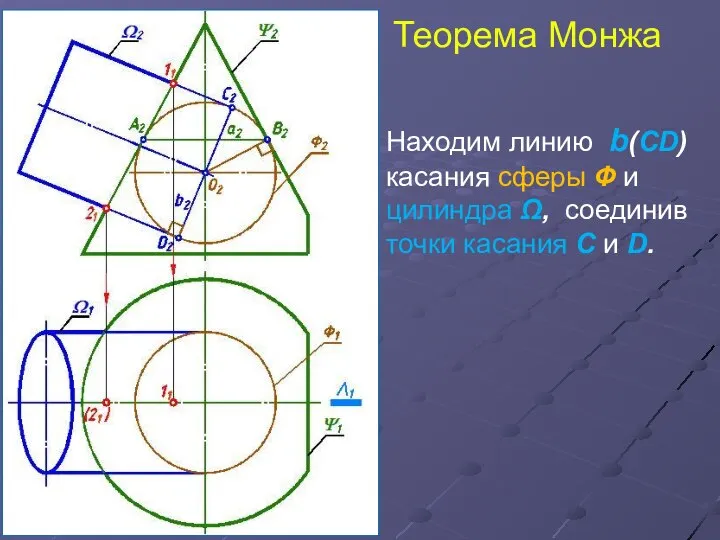
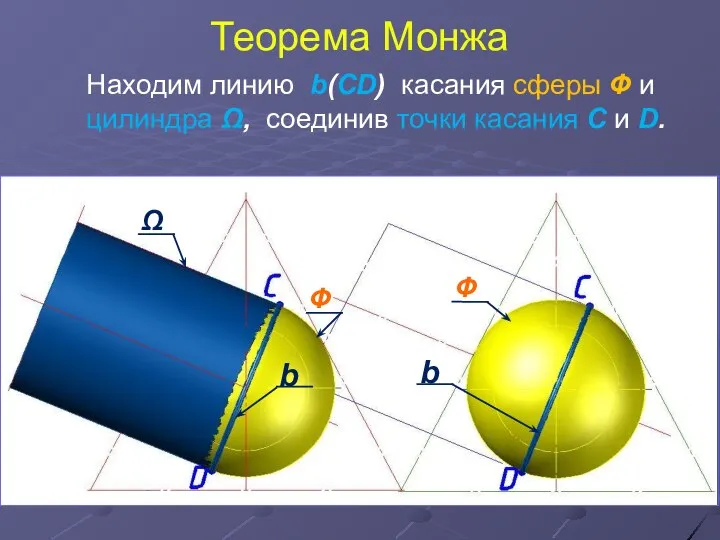
- 9. Теорема Монжа Находим линию b(СD) касания сферы Ф и цилиндра Ω, соединив точки касания С и
- 10. Теорема Монжа Находим линию b(СD) касания сферы Ф и цилиндра Ω, соединив точки касания С и
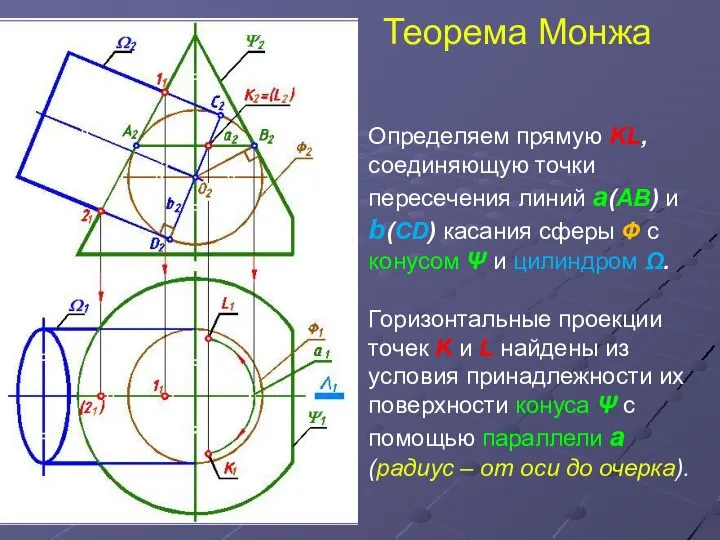
- 11. Теорема Монжа Определяем прямую KL, соединяющую точки пересечения линий а(АВ) и b(СD) касания сферы Ф с
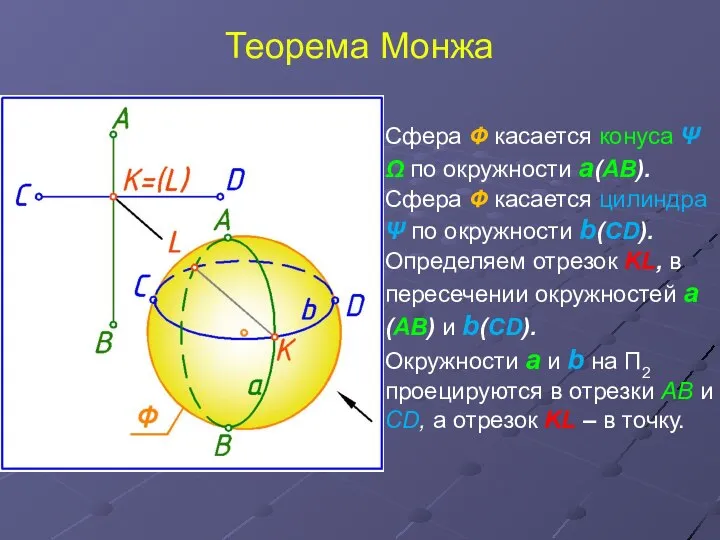
- 12. Теорема Монжа Сфера Ф касается конуса Ψ Ω по окружности а(АВ). Сфера Ф касается цилиндра Ψ
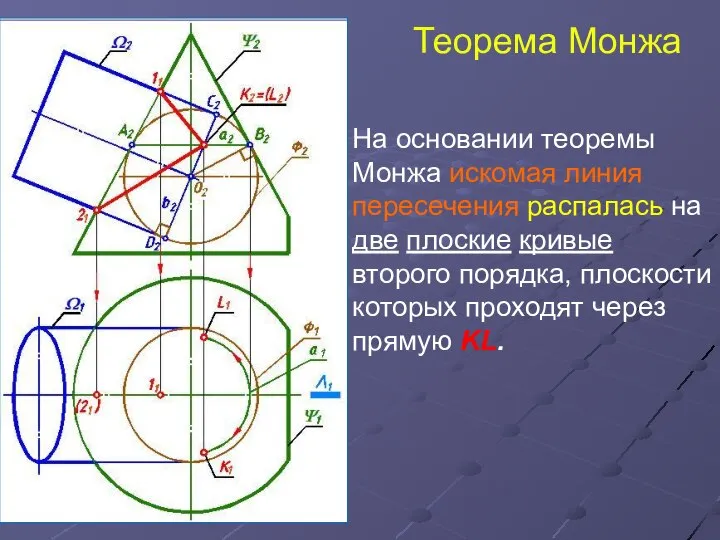
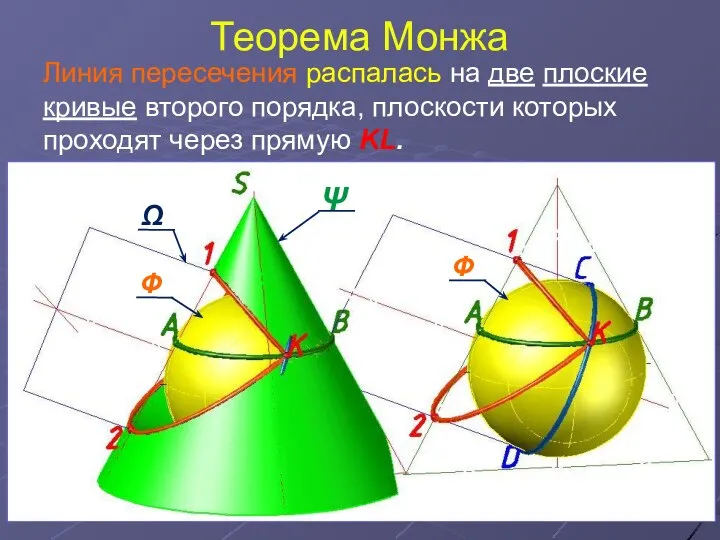
- 13. Теорема Монжа На основании теоремы Монжа искомая линия пересечения распалась на две плоские кривые второго порядка,
- 14. Теорема Монжа Линия пересечения распалась на две плоские кривые второго порядка, плоскости которых проходят через прямую
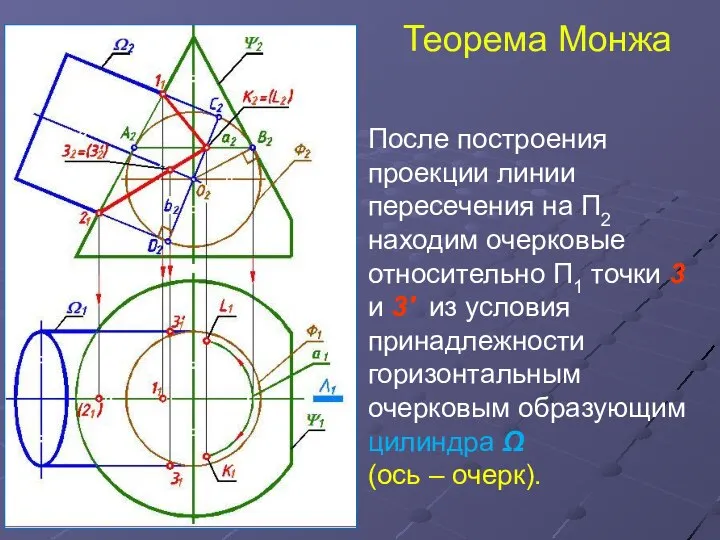
- 15. Теорема Монжа После построения проекции линии пересечения на П2 находим очерковые относительно П1 точки 3 и
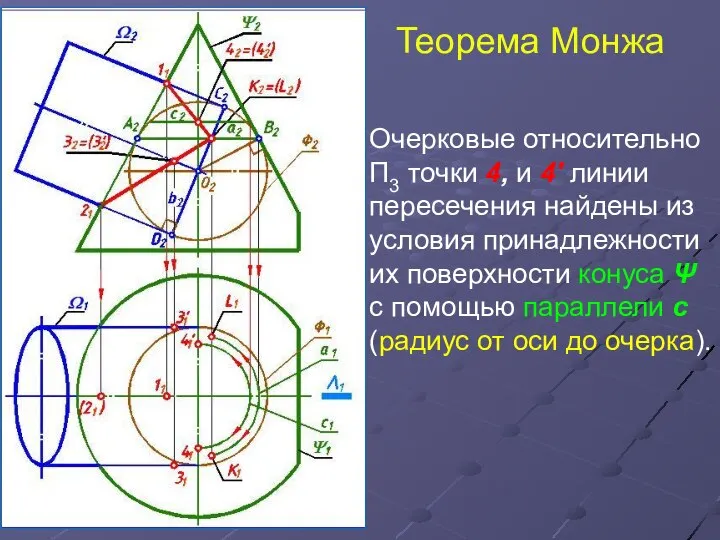
- 16. Теорема Монжа Очерковые относительно П3 точки 4, и 4' линии пересечения найдены из условия принадлежности их
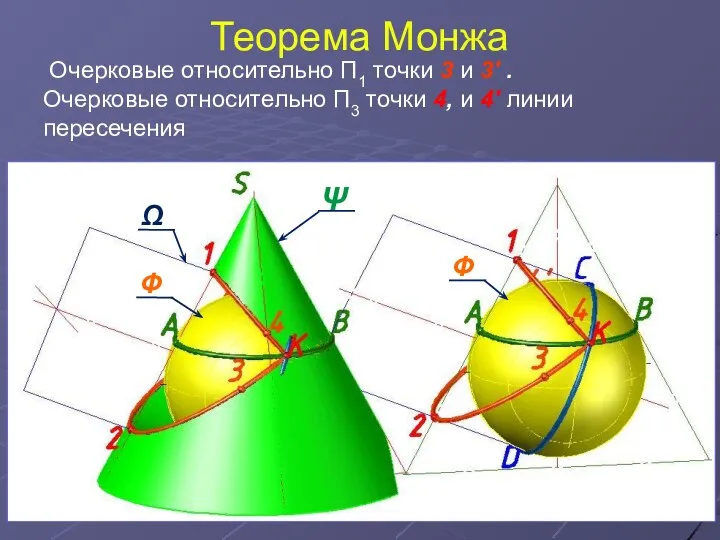
- 17. Теорема Монжа Очерковые относительно П1 точки 3 и 3' . Очерковые относительно П3 точки 4, и
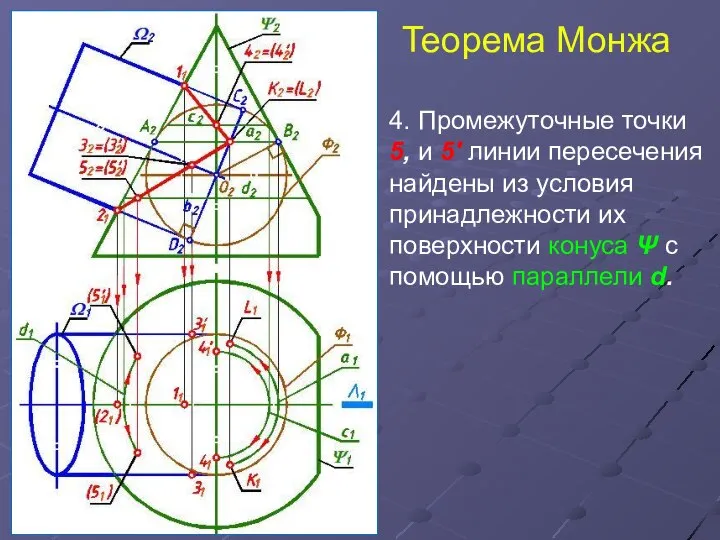
- 18. Теорема Монжа 4. Промежуточные точки 5, и 5' линии пересечения найдены из условия принадлежности их поверхности
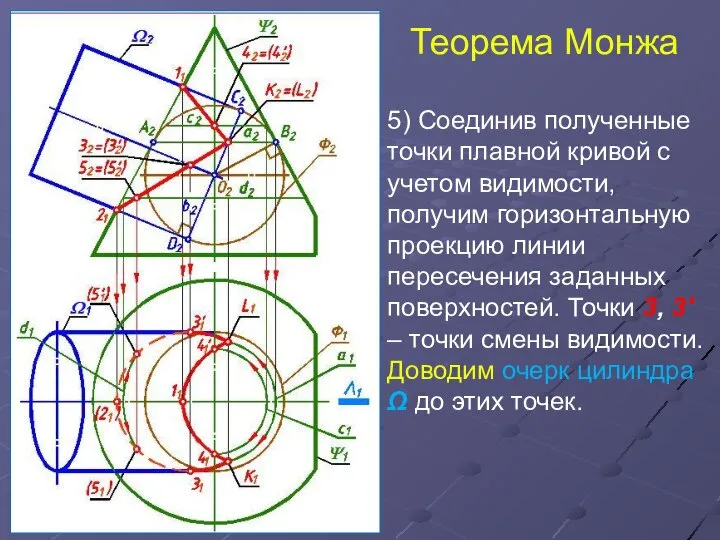
- 19. Теорема Монжа 5) Соединив полученные точки плавной кривой с учетом видимости, получим горизонтальную проекцию линии пересечения
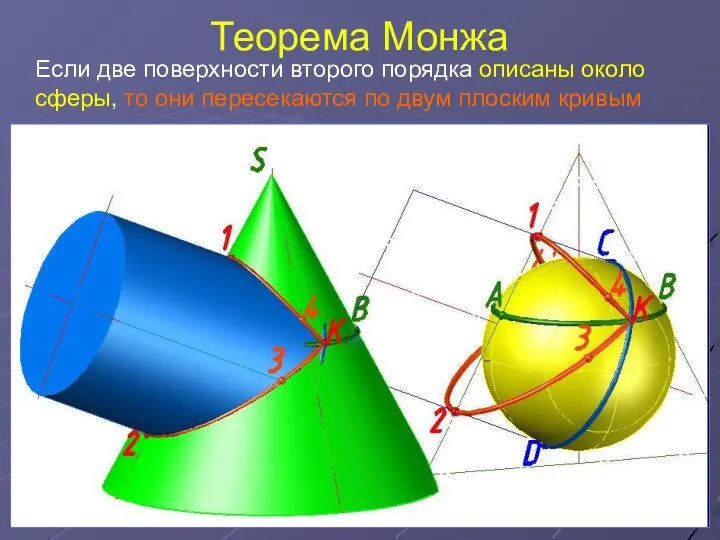
- 20. Теорема Монжа Если две поверхности второго порядка описаны около сферы, то они пересекаются по двум плоским
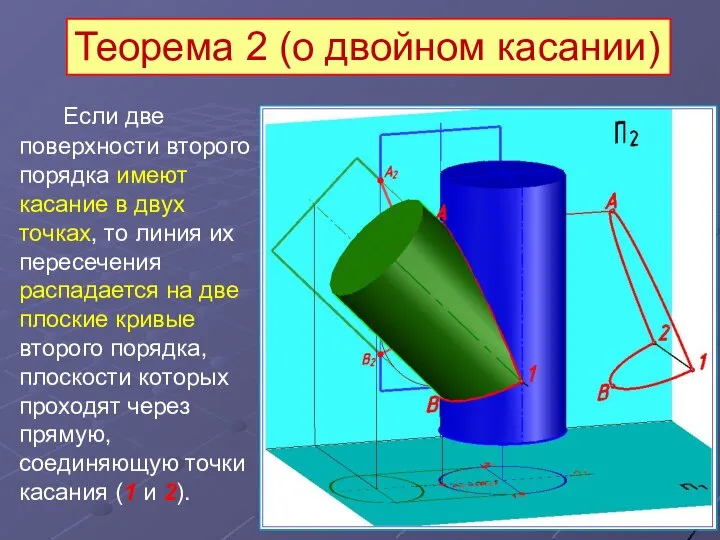
- 21. Если две поверхности второго порядка имеют касание в двух точках, то линия их пересечения распадается на
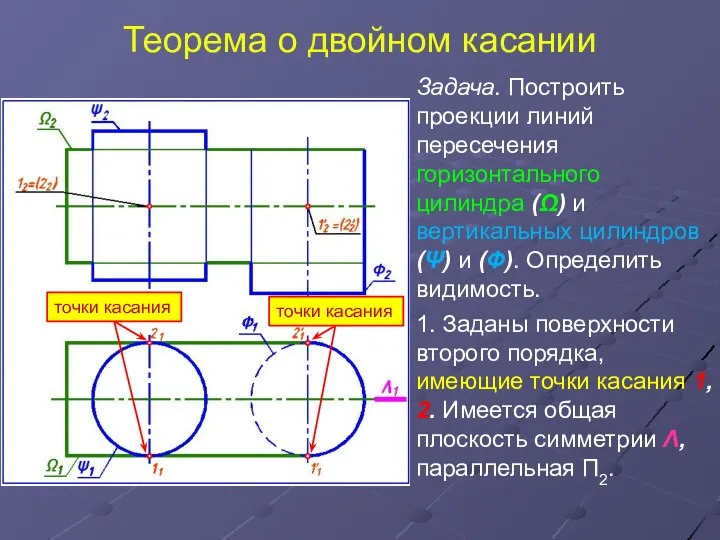
- 22. Теорема о двойном касании Задача. Построить проекции линий пересечения горизонтального цилиндра (Ω) и вертикальных цилиндров (Ψ)
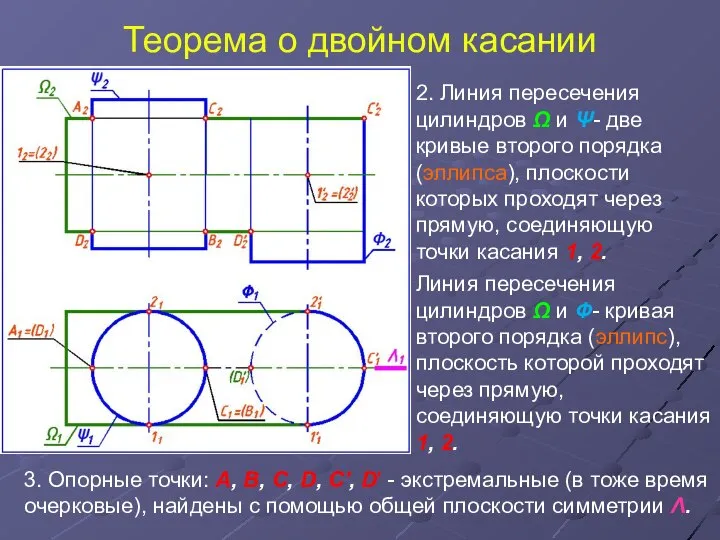
- 23. Теорема о двойном касании 2. Линия пересечения цилиндров Ω и Ψ- две кривые второго порядка (эллипса),
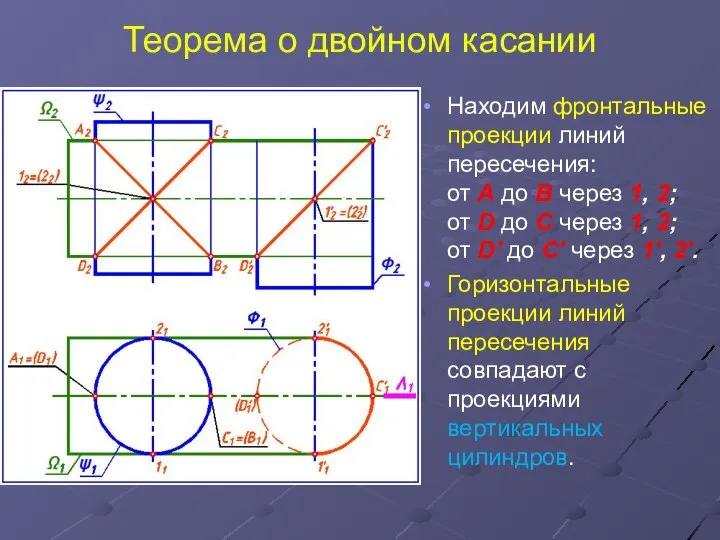
- 24. Теорема о двойном касании Находим фронтальные проекции линий пересечения: от А до В через 1, 2;
- 26. Скачать презентацию
 Техническая изоляция
Техническая изоляция История развития процессора
История развития процессора Глава 2. Экономика домохозяйства § 13. Благосостояние
Глава 2. Экономика домохозяйства § 13. Благосостояние  Формы предпринимательской деятельности. Экономика. 10 класс. Автор: Бондарь Ольга Николаевна, МОУ СОШ №2 ст. Медведовская МО Т
Формы предпринимательской деятельности. Экономика. 10 класс. Автор: Бондарь Ольга Николаевна, МОУ СОШ №2 ст. Медведовская МО Т Фрагменты видеолекций по начертательной геометрии
Фрагменты видеолекций по начертательной геометрии  История и основные понятия науки о материалах
История и основные понятия науки о материалах Грибковые поражения слизистой оболочки полости рта. Этиология, патогенез, диагностика, лечения и профилактика.
Грибковые поражения слизистой оболочки полости рта. Этиология, патогенез, диагностика, лечения и профилактика.  «ЧУВАШСКАЯ ВЫШИВКА – БОГАТЕЙШЕЕ ИСКУССТВО» Выполнила: Чувашова Ольга Руководитель: учитель Технологии Сагдеева Алё
«ЧУВАШСКАЯ ВЫШИВКА – БОГАТЕЙШЕЕ ИСКУССТВО» Выполнила: Чувашова Ольга Руководитель: учитель Технологии Сагдеева Алё Модель корпоративного управления
Модель корпоративного управления Презентация Европейская валютная система
Презентация Европейская валютная система Улыбнись этой жизни
Улыбнись этой жизни The military and politics
The military and politics Оказание первой медицинской помощи (часть 3 - ГУМ)
Оказание первой медицинской помощи (часть 3 - ГУМ)  Вероучение и богослужение Православной Церкви. Учение о таинствах
Вероучение и богослужение Православной Церкви. Учение о таинствах Имидж делового мужчины
Имидж делового мужчины МХК 5 класс Зачет по теме: «Аполлон и музы Парнаса»
МХК 5 класс Зачет по теме: «Аполлон и музы Парнаса» Элементы линейной и векторной алгебры - презентация по Алгебре
Элементы линейной и векторной алгебры - презентация по Алгебре Презентация на тему "Развитие устной речи у младших школьников с ограниченными возможностями здоровья" - скачать презентации
Презентация на тему "Развитие устной речи у младших школьников с ограниченными возможностями здоровья" - скачать презентации 182f0c819a364dc68d63814a38c94c47 (1)
182f0c819a364dc68d63814a38c94c47 (1) История ландшафта
История ландшафта Основные изменения в брачно-семейном и уголовном праве США в Новейшее время
Основные изменения в брачно-семейном и уголовном праве США в Новейшее время  МЕТОДИКА И ОРГАНИЗАЦИЯ СОЦИАЛЬНО – КУЛЬТУРНОГО ТВОРЧЕСТВА
МЕТОДИКА И ОРГАНИЗАЦИЯ СОЦИАЛЬНО – КУЛЬТУРНОГО ТВОРЧЕСТВА Кейс по внедрению CRM в гостинично-ресторанный комплекс «Жемчужина»
Кейс по внедрению CRM в гостинично-ресторанный комплекс «Жемчужина» Экономические теории о функции и роли денег в экономике ВЫПОЛНИЛИ СТУДЕНТКИ 4 КУРСА МИЛОСЕРДОВА А.Г И АЛЕКСЕЕВА А.А.
Экономические теории о функции и роли денег в экономике ВЫПОЛНИЛИ СТУДЕНТКИ 4 КУРСА МИЛОСЕРДОВА А.Г И АЛЕКСЕЕВА А.А. Фотопрактикум
Фотопрактикум Футбольный клуб “Манчестер Юнайтед”
Футбольный клуб “Манчестер Юнайтед” М.М. Поташник, М.В. Левит Презентацию выполнила Н.П.Мастюгина, заместитель директора по УВР
М.М. Поташник, М.В. Левит Презентацию выполнила Н.П.Мастюгина, заместитель директора по УВР Презентация Основы научных исследований разминка
Презентация Основы научных исследований разминка