Пограничный слой

соизмеримы с силами инерции!

— 1953гг.

- уравнения пограничного слоя Прандтля (1904г.)

Уравнения пограничного слоя Прандтля (4.2) – незамкнуты: неизвестны компоненты скорости и давление; Прандтль предложил в первом приближении не учитывать обратного влияния погранслоя на внешний поток; поскольку толщина погранслоя мала, то распределение давления и скорости можно взять из внешнего (вне погранслоя) течения). Поскольку вне погранслоя течение потенциальное, то можно записать уравнение Бернулли:

(4.2)

x

у

Потенциальное течение

Окончательно получаем уравнения Прандтля в форме:

плоской стенки, но и в более сложных случаях геометрии тел

Уравнения пограничного слоя Прандтля (1904г.)

Если ввести безразмерные переменные:

- скорость на бесконечности; тогда

(4.5)

означает, что решения этих уравнений не содержат числа Рейнольдса. Таким образом, течение в пограничном слое при изменении числа Рейнольдса изменяется подобна сама себе: продольные расстояния и скорости остаются неизменными, а поперечные меняются обратно пропорционально корню из числа Рейнольдса!

Кроме того, нетрудно показать, что:

Отношение поперечной скорости к продольной обратно пропорционально !

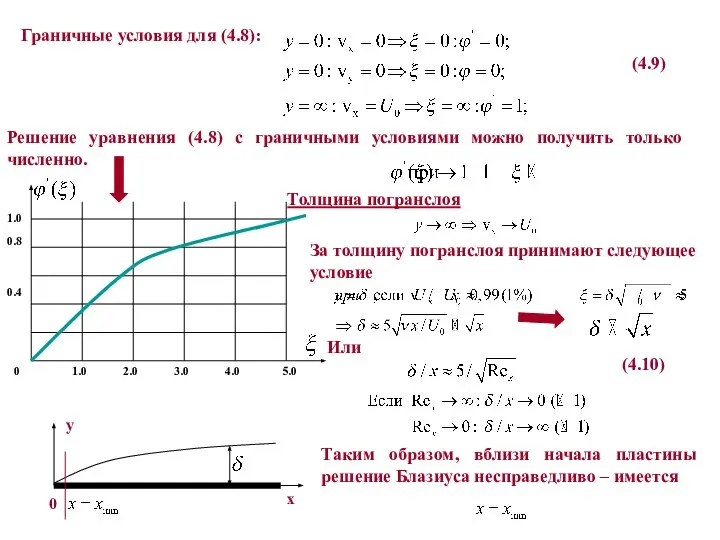
При этом толщина погранслоя есть

(4.6)

задачу о погранслое на плоской полубесконечной пластине

x

y

0

Пусть скорость основного потока равна:

В задаче о полубесконечной пластине нет никаких характерных параметров длины; отсюда введем следующие величины:

Тогда из уравнений (4.3) следует:

(4.7)

Вводим функцию тока:

только численно.

0.4

0.8

1.0

5.0

4.0

3.0

2.0

1.0

0

Толщина погранслоя

За толщину погранслоя принимают следующее условие

y

0

x

Или

(4.10)

Таким образом, вблизи начала пластины решение Блазиуса несправедливо – имеется