Содержание
- 2. Лекция 2.1 Два определения предела функции в точке, их эквивалентность. Критерий Коши существования предела функции. Односторонние
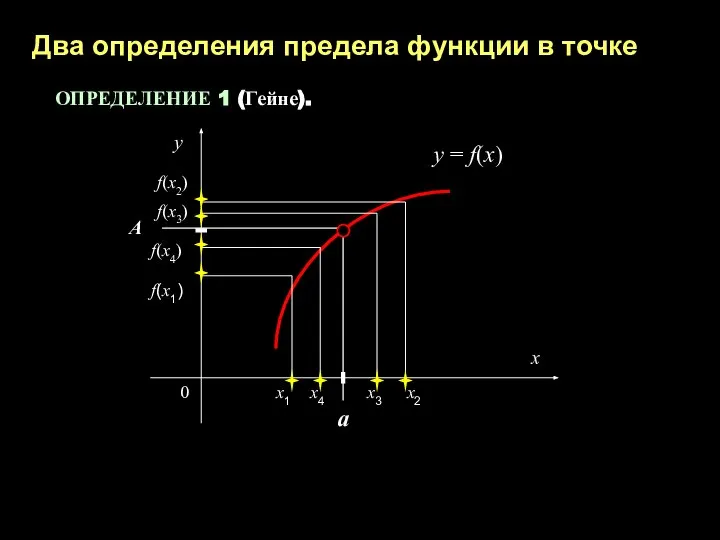
- 3. Два определения предела функции в точке ОПРЕДЕЛЕНИЕ 1 (Гейне). x1 a A f(x1) x2 x3 x4
- 4. Пусть функция f(x) определена в Число А называется пределом функции f(x) в точке а, если для
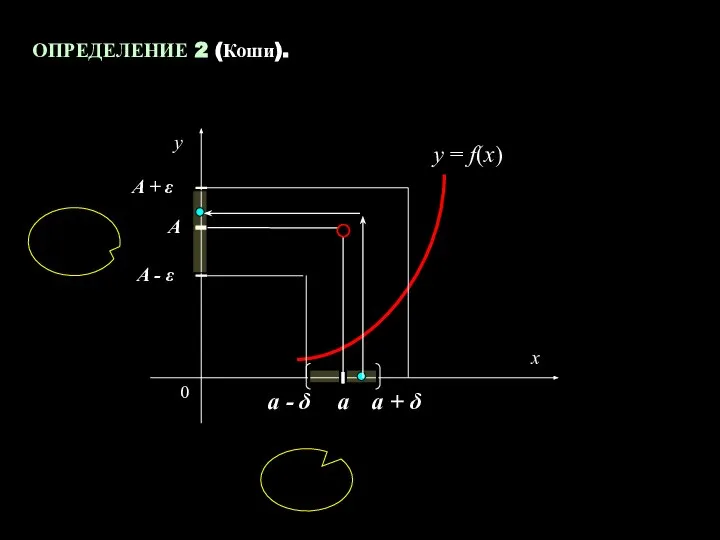
- 5. ОПРЕДЕЛЕНИЕ 2 (Коши). a A x y y = f(x) 0 A - ε A +
- 6. Пусть функция f(x) определена в Число А называется пределом функции f(x) в точке а, если для
- 7. ТЕОРЕМА. Два определения предела функции, по Коши и по Гейне, эквивалентны.
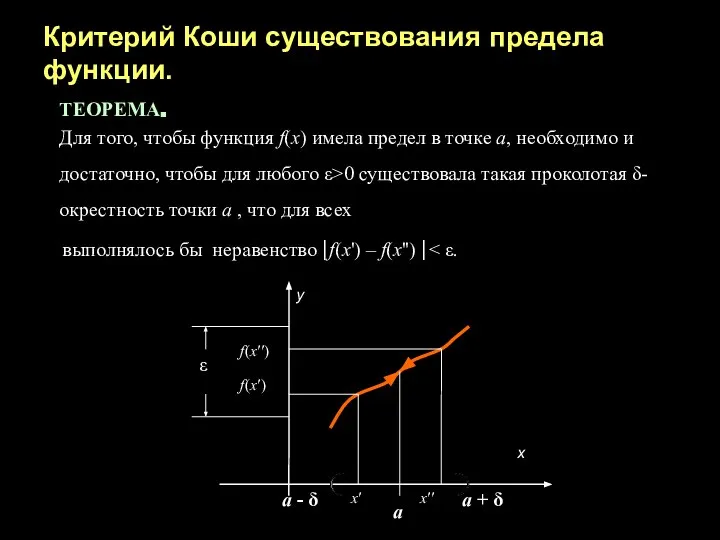
- 8. Критерий Коши существования предела функции. ТЕОРЕМА. Для того, чтобы функция f(x) имела предел в точке а,
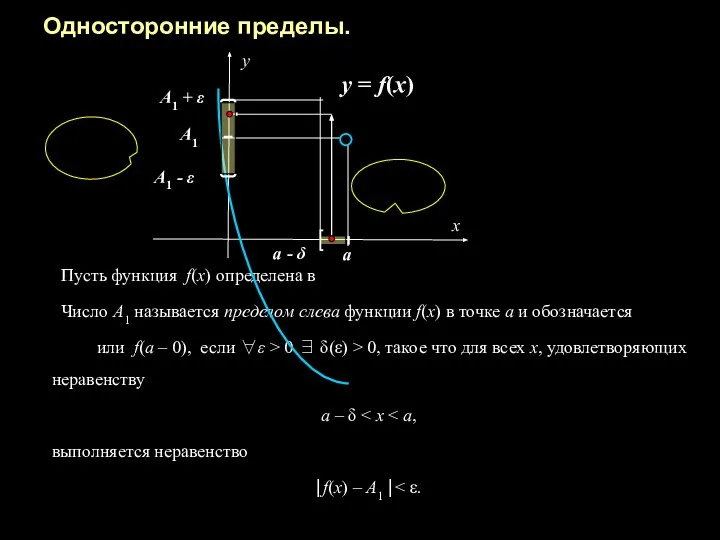
- 9. Односторонние пределы. Пусть функция f(x) определена в Число А1 называется пределом слева функции f(x) в точке
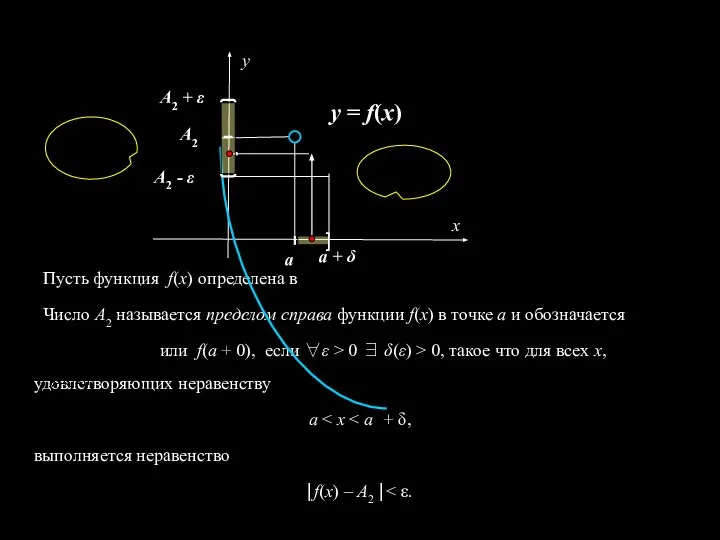
- 10. Пусть функция f(x) определена в Число А2 называется пределом справа функции f(x) в точке а и
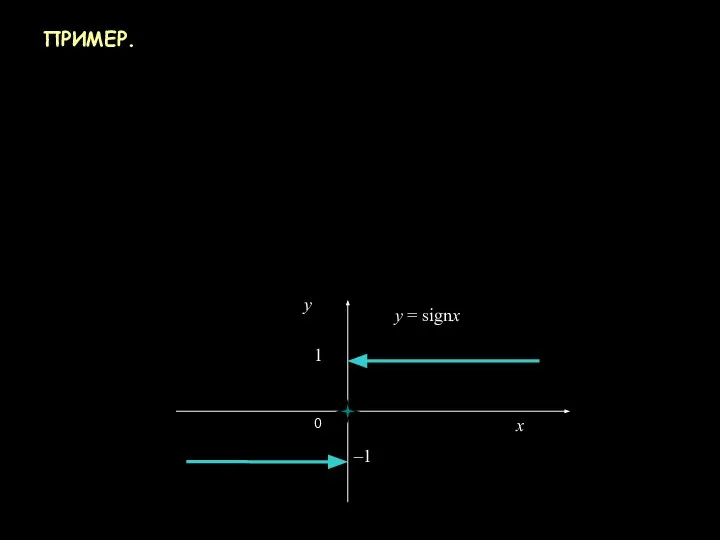
- 11. ПРИМЕР.
- 12. ТЕОРЕМА. Для существования необходимо и достаточно, чтобы существовали пределы этой функции в точке а слева и
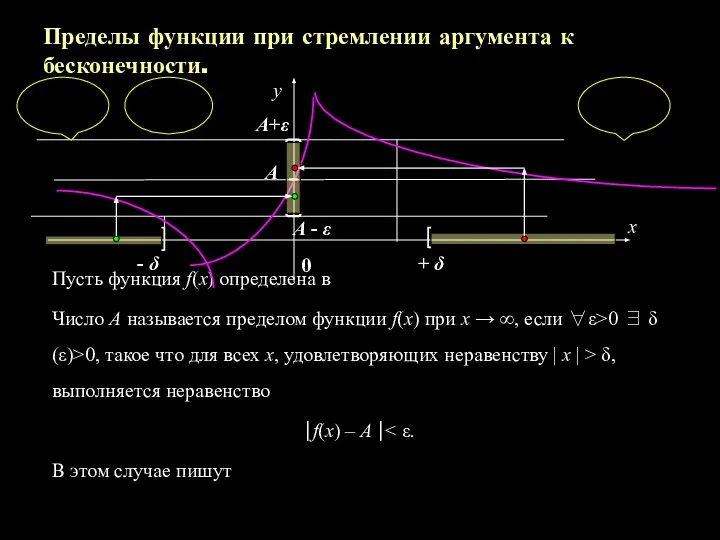
- 13. Пределы функции при стремлении аргумента к бесконечности. Пусть функция f(x) определена в Число А называется пределом
- 14. Бесконечно малые и бесконечно большие функции. ОПРЕДЕЛЕНИЕ 1. Функция α(х) называется бесконечно малой при стремлении аргумента
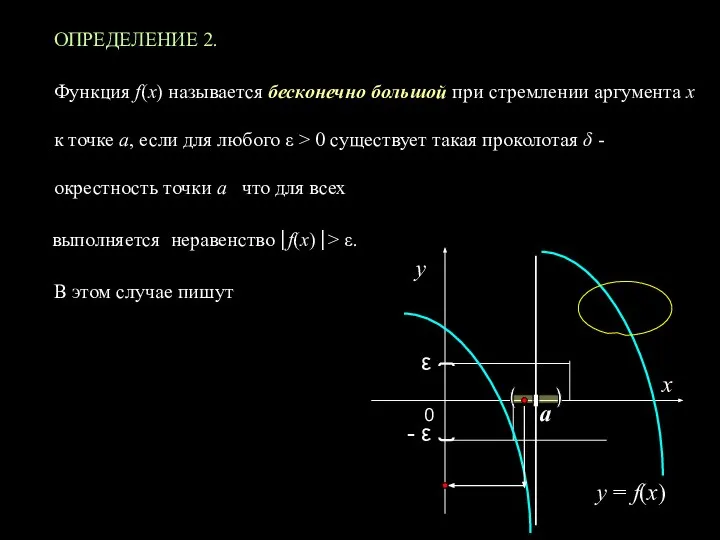
- 15. ОПРЕДЕЛЕНИЕ 2. Функция f(х) называется бесконечно большой при стремлении аргумента х к точке а, если для
- 16. Аналогично определяются пределы а также пределы
- 17. Свойства бесконечно малых и бесконечно больших функций. Алгебраическая сумма конечного числа бесконечно малых при х→ а
- 19. Скачать презентацию








 Функции таможенных органов Работу выполнил Студент группы Т-111 Бобырь Алексей
Функции таможенных органов Работу выполнил Студент группы Т-111 Бобырь Алексей The political system of Great Britain
The political system of Great Britain Завод «Кундуз» Презентация медиа-кампании
Завод «Кундуз» Презентация медиа-кампании Готов к труду и обороне
Готов к труду и обороне Закон Вебера-Фехнера
Закон Вебера-Фехнера Suomen kielen tunnit
Suomen kielen tunnit St. Valentine’s Day
St. Valentine’s Day Олимпийское движение в Беларуси
Олимпийское движение в Беларуси Государственная кадастровая оценка земель сельскохозяйственного назначения. Методическое и технологическое обеспечение оценки
Государственная кадастровая оценка земель сельскохозяйственного назначения. Методическое и технологическое обеспечение оценки Теория Жана Пиаже
Теория Жана Пиаже Выполнение основных операций штукатурных процессов
Выполнение основных операций штукатурных процессов Современные материалы в строительстве
Современные материалы в строительстве Тайны грибного царства - презентация для начальной школы_
Тайны грибного царства - презентация для начальной школы_ Опусти свой стакан
Опусти свой стакан Герои сошли со страниц литературных произведений Презентация на тему:_
Герои сошли со страниц литературных произведений Презентация на тему:_ Форма государства Политическая система общества
Форма государства Политическая система общества Презентация "Профессия – «Экономист»" - скачать презентации по Экономике
Презентация "Профессия – «Экономист»" - скачать презентации по Экономике Стандарт OpenMP. Информационные ресурсы. Лекция 3
Стандарт OpenMP. Информационные ресурсы. Лекция 3 Презентация на тему История появления бисера
Презентация на тему История появления бисера  Internet tracking
Internet tracking Ислам
Ислам Иван Константинович Айвазовский (1817-1900)
Иван Константинович Айвазовский (1817-1900) Управление моделями в UML
Управление моделями в UML «С» - [s] [k]
«С» - [s] [k] Термодинамический потенциал в переменных S, V
Термодинамический потенциал в переменных S, V Коммерческое предложение для партнёров
Коммерческое предложение для партнёров Понятие психология Выполнила: студентка 1-ого курса ФТД группа Т-116 Цьопа Дарья
Понятие психология Выполнила: студентка 1-ого курса ФТД группа Т-116 Цьопа Дарья Maria Hoefl-Riesch. Bekannte deutsche Sportlerin
Maria Hoefl-Riesch. Bekannte deutsche Sportlerin