Содержание
- 2. Свойства функций, имеющих предел. ТЕОРЕМА 1. Если функция f(x) имеет предел в точке а, то найдется
- 3. ТЕОРЕМА 2. Если функция f(x) имеет в точке а предел, отличный от нуля, то найдется такая
- 4. ТЕОРЕМА 3. Если f (x) ≥ 0 в некоторой проколотой окрестности точки а и то А
- 5. ТЕОРЕМА 4. (О двух милиционерах.) Если в некоторой проколотой окрестности точки а справедливы неравенства f(x) ≤
- 6. ТЕОРЕМА 5. Если f(x) = с – постоянная в некоторой проколотой окрестности точки а, то Если
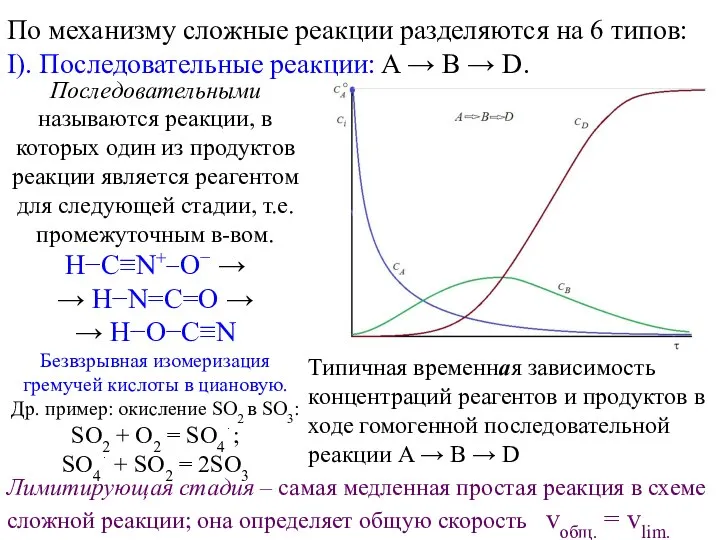
- 7. ДОКАЗАТЕЛЬСТВО. Воспользуемся определением предела по Гейне. Возьмем ЧП сходящуюся к а. Тогда f(xn) = с для
- 8. СЛЕДСТВИЯ из теорем 3, 5. Если f(x) ≥ В в некоторой проколотой окрестности точки а и
- 9. Арифметика бесконечностей. Введем обозначения: С = const ≠ 0. ∞ – бесконечно большая функция произвольного знака;
- 10. Неопределенные ситуации, требующие исследования. 0/0 0⋅∞ ∞/∞ ∞ – ∞ 1∞ 00 ∞0
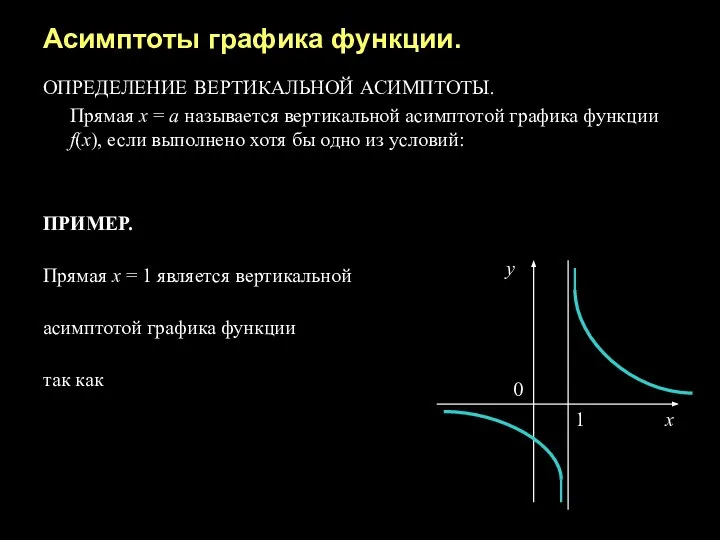
- 11. Асимптоты графика функции. ОПРЕДЕЛЕНИЕ ВЕРТИКАЛЬНОЙ АСИМПТОТЫ. Прямая х = а называется вертикальной асимптотой графика функции f(x),
- 12. ОПРЕДЕЛЕНИЕ НАКЛОННОЙ АСИМПТОТЫ. Прямая у = kx + b называется наклонной асимптотой графика функции f(x) при
- 13. Доказательство. Пусть Тогда f(x) – (kx + b) = α(х), где α(х) бесконечно малая при х→
- 14. Пусть Тогда f(x) – (kx + b) = (f(x) –kx) – b = b+ α(х) –
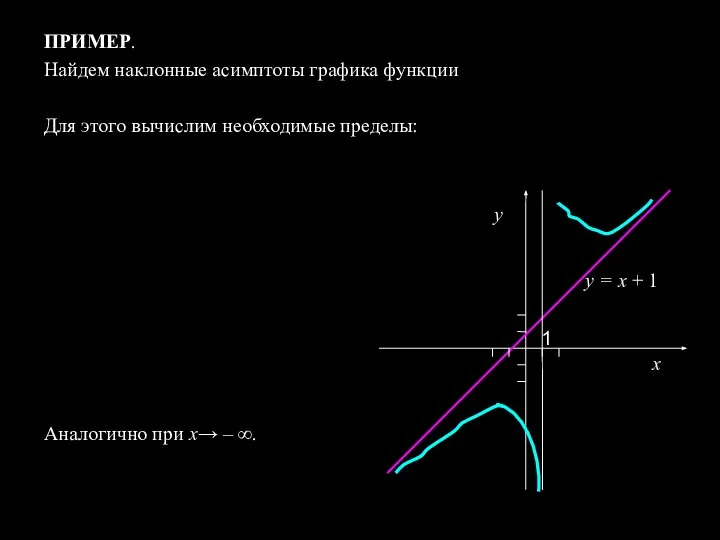
- 15. ПРИМЕР. Найдем наклонные асимптоты графика функции Для этого вычислим необходимые пределы: Аналогично при х→ – ∞.
- 17. Скачать презентацию












 лекция_4_2019_20
лекция_4_2019_20 Недействительность сделки, совершенной под влиянием заблуждения
Недействительность сделки, совершенной под влиянием заблуждения Основные понятия о государстве и политической системе
Основные понятия о государстве и политической системе Понятие и структура правовой системы
Понятие и структура правовой системы  Развитие маркетинга в Китае Подготовила: Клеутина Светлана ДС_01
Развитие маркетинга в Китае Подготовила: Клеутина Светлана ДС_01  Boża Matka
Boża Matka Бағдарламалау технологиясының тарихи аспектісі. Негізгі түсініктер мен анықтамалар
Бағдарламалау технологиясының тарихи аспектісі. Негізгі түсініктер мен анықтамалар Phase structure of competitive activity of the athlete
Phase structure of competitive activity of the athlete Кейс «Тайленол» на основе материалов Effie Awards
Кейс «Тайленол» на основе материалов Effie Awards Анализ основных достижений ученых досоветского периода
Анализ основных достижений ученых досоветского периода Барокко
Барокко .1_Аналгезирующие средства
.1_Аналгезирующие средства Проект « Профессии наших родителей» УЧЕНИКОВ 4 Б МОУ «ЛИЦЕЙ № 13»
Проект « Профессии наших родителей» УЧЕНИКОВ 4 Б МОУ «ЛИЦЕЙ № 13» Эдом
Эдом Правила проектирования печатных плат
Правила проектирования печатных плат Символы христианства. Богослужебная утварь
Символы христианства. Богослужебная утварь Понятие уголовной ответственности
Понятие уголовной ответственности Введение в инженерный анализ методом конечных элементов. Реализация в Solid Edge Simulation/Express
Введение в инженерный анализ методом конечных элементов. Реализация в Solid Edge Simulation/Express Форма государственного устройства
Форма государственного устройства Портал недвижимости для собственников и профессионалов Primarkt.Ru
Портал недвижимости для собственников и профессионалов Primarkt.Ru Минимизация логических функций
Минимизация логических функций Оздоровительный проект «Черлидинг- детям»
Оздоровительный проект «Черлидинг- детям» Свёртывание крови
Свёртывание крови  Аудармашының заңды статусы
Аудармашының заңды статусы ДРОФА И СТРЕПЕТ, занесённые в Красную книгу Саратовской области. Учебная презентация учащихся 4 класса МОУ «СОШ с.Багаевка»: Михее
ДРОФА И СТРЕПЕТ, занесённые в Красную книгу Саратовской области. Учебная презентация учащихся 4 класса МОУ «СОШ с.Багаевка»: Михее Презентация на тему "Родительские директивы" - скачать презентации по Педагогике
Презентация на тему "Родительские директивы" - скачать презентации по Педагогике Стоматологиядағы менеджмент және маркетинг негіздері
Стоматологиядағы менеджмент және маркетинг негіздері Организационный контекст: стратегия, структура и культура. Лекция 3
Организационный контекст: стратегия, структура и культура. Лекция 3