Содержание
- 2. В узком смысле слова под законом больших чисел понимается ряд математических теорем, которые утверждают приближение средних
- 3. Пусть Х - случайная величина с мат. ожиданием mx и дисперсией Dx. Тогда для любого ε>0
- 4. НЕРАВЕНСТВО ЧЕБЫШЕВА
- 5. Предположим, что случайная величина Х дискретна и ее ряд распределения имеет вид: Запишем дисперсию этой СВ:
- 6. Тогда дисперсия окажется больше полученной суммы: Делаем замену: Тогда неравенство сохраняется: Последняя сумма представляет собой вероятность
- 7. Следовательно неравенство примет вид: Откуда окончательно получаем:
- 8. ТЕОРЕМА ЧЕБЫШЕВА Пусть Х -СВ с математическим ожиданием a и дисперсией d. Будем проводить серии из
- 10. КОММЕНТАРИЙ Если проводятся серии из n опытов, то от одной серии к другой, среднее арифметическое СВ
- 11. Говорят, что при достаточно большом числе опытов среднее арифметическое наблюдаемых значений случайной величины сходится по вероятности
- 12. Пусть Хi - значение, принятое случайной величиной Х в i-ом опыте. Чтобы найти среднее арифметическое значений
- 13. Все величины Хi распределены как случайная величина Х. Следовательно, M[Xi]=M[X]=a Так как опыты проводятся независимо, то
- 14. Все величины Хi распределены как случайная величина Х. Следовательно, D[Xi]=D[X]=d Применим неравенство Чебышева:
- 15. В качестве СВ Х подставим Yn : Подставляем найденное значение математического ожидания и дисперсии: Величина при
- 16. Следствием закона больших чисел является теорема Я. Бернулли. Она устанавливает связь между частотой события и его
- 17. ТЕОРЕМА БЕРНУЛЛИ Пусть событие А происходит в опыте с вероятностью р. Будем проводить серии из n
- 19. КОММЕНТАРИЙ Если проводятся серии из n опытов, то от одной серии к другой, частота события будет
- 20. Пусть Х - случайная величина, которая равна 1, если событие А произошло в опыте и равна
- 21. Частота γn представляет собой величину А это есть среднее арифметическое величины. Согласно закону больших чисел эта
- 22. ЦЕНТРАЛЬНАЯ ПРЕДЕЛЬНАЯ ТЕОРЕМА ЦПТ устанавливает условия, при которых возникает самый распространенный закон распределения - нормальный закон.
- 23. Поэтому отклонение снаряда от цели обусловлено суммой всех элементарных отклонений. Поскольку этих факторов очень много и
- 24. Если Х1, Х2... Хn - независимые случайные величины, имеющие один и тот же закон распределения с
- 25. Практически, ЦПТ можно пользоваться, когда число слагаемых в сумме невелико, порядка 10 или еще меньше. ЦПТ
- 26. попадает в интервал от α до β выражается формулой где mz , σz - математическое ожидание
- 27. То есть, чтобы приближенно найти вероятность попадания суммы большого числа случайных величин на заданный участок, не
- 28. Если закон распределения величины Z близок к нормальному с параметрами mz σz , то закон распределения
- 29. Если величины Х1 Х2... Хn – дискретны, то их сумма тоже дискретная случайная величина. Строго говоря,
- 30. M[Z90]=20·90=1800, D[Z90]= 200·90=18000 Сумма величин Z90=ΣXi за квартал будет распределена по нормальному закону c параметрами Следовательно,
- 31. Частным случаем ЦПТ для дискретных случайных величин является Пусть событие А происходит с вероятностью р. Будем
- 33. Скачать презентацию


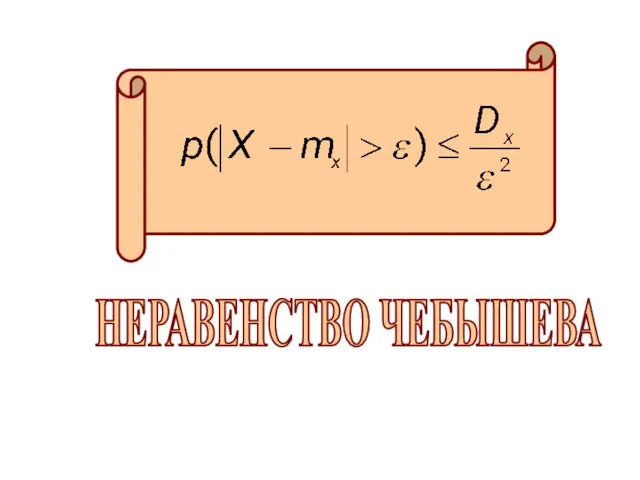




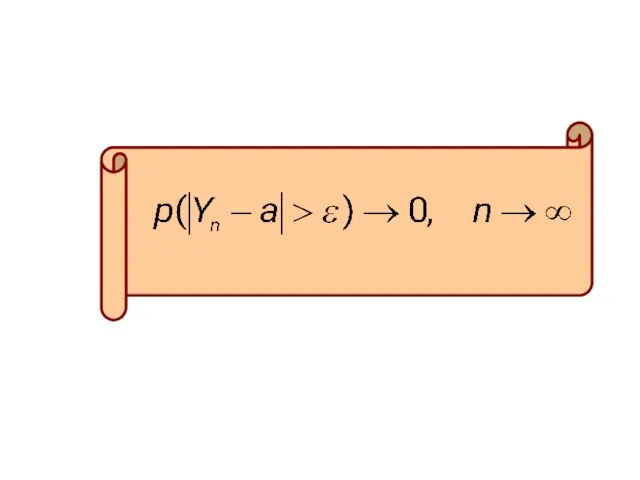



![Все величины Хi распределены как случайная величина Х. Следовательно, M[Xi]=M[X]=a Так](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1230147/slide-12.jpg)
![Все величины Хi распределены как случайная величина Х. Следовательно, D[Xi]=D[X]=d Применим неравенство Чебышева:](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1230147/slide-13.jpg)



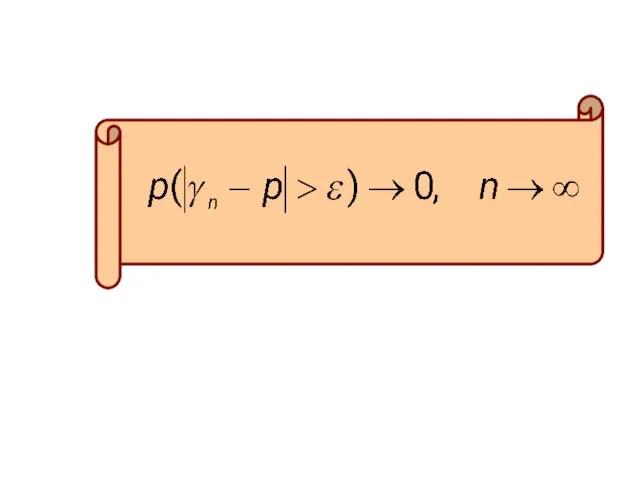











![M[Z90]=20·90=1800, D[Z90]= 200·90=18000 Сумма величин Z90=ΣXi за квартал будет распределена по](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1230147/slide-29.jpg)

 Политическая культура
Политическая культура Преобразование комплексного чертежа
Преобразование комплексного чертежа Зимові народні свята січня
Зимові народні свята січня Приложение 3. XIV фестиваль искусств детей и юношества им Д.Б. Кабалевского
Приложение 3. XIV фестиваль искусств детей и юношества им Д.Б. Кабалевского «Квотирование товаров как мера нетарифного регулирования внешней торговли товарами» Выполнила: Студентка V курса Группы ДС 02.2 З
«Квотирование товаров как мера нетарифного регулирования внешней торговли товарами» Выполнила: Студентка V курса Группы ДС 02.2 З Социально-биологические основы физической культуры и здоровья
Социально-биологические основы физической культуры и здоровья Бойове застосування КЗА 86Ж6. Призначення та структурна схема комплексу програм КЗА 86Ж6. (Тема 8.1)
Бойове застосування КЗА 86Ж6. Призначення та структурна схема комплексу програм КЗА 86Ж6. (Тема 8.1) Метод Дельфи (Delphi)
Метод Дельфи (Delphi) Бурнаковка 2020. Проект образцового микрорайона
Бурнаковка 2020. Проект образцового микрорайона Критическое мышление
Критическое мышление Презентация "Портрет" - скачать презентации по МХК
Презентация "Портрет" - скачать презентации по МХК Мен және заң
Мен және заң Кинематический анализ механизмов
Кинематический анализ механизмов Баскетбол - командная спортивная игра
Баскетбол - командная спортивная игра Суд и процесс по Салической правде Подготовили студенты Трунин Сергей и Казьмин Георгий Ю-
Суд и процесс по Салической правде Подготовили студенты Трунин Сергей и Казьмин Георгий Ю- Футболисты мира
Футболисты мира Форма для заполнения клиента компании ASD Хозмаг
Форма для заполнения клиента компании ASD Хозмаг Костюм Италии эпохи Кватроченто
Костюм Италии эпохи Кватроченто Исторически сложившиеся системы и концепции профессионального образования
Исторически сложившиеся системы и концепции профессионального образования Международный терроризм как глобальная геополитическая проблема
Международный терроризм как глобальная геополитическая проблема НОВОСТИ Фунтикова Хропина
НОВОСТИ Фунтикова Хропина Повышение правовой культуры граждан – социальная миссия библиотеки
Повышение правовой культуры граждан – социальная миссия библиотеки Основные конструкции языка VBA
Основные конструкции языка VBA тренажер Буква потерялась - презентация для начальной школы
тренажер Буква потерялась - презентация для начальной школы Основы системного анализа 5
Основы системного анализа 5 Урок-концерт на тему «Из истории авторской песни»
Урок-концерт на тему «Из истории авторской песни» Общие принципы построения и использования языков программирования. Компьютерная память. Работа с данными в языках программирован
Общие принципы построения и использования языков программирования. Компьютерная память. Работа с данными в языках программирован Марс
Марс