Содержание
- 2. и тогда многочлен (1) примет вид: Многочлен, который в n+1 узловой точке будет принимать заданные значения,
- 3. Пример. По заданным точкам Определить интерполяционный многочлен L(x). L(x)=x2
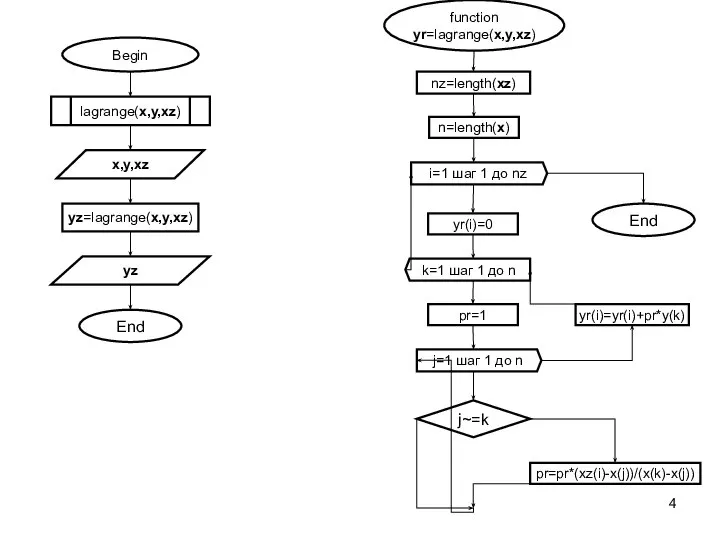
- 4. function yr=lagrange(x,y,xz) n=length(x) nz=length(xz) i=1 шаг 1 до nz k=1 шаг 1 до n j=1 шаг
- 5. Метод наименьших квадратов Пусть данные некоторого эксперимента представлены в виде таблицы значений независимой переменной x и
- 6. Функцию f(x,a0,a1,…,am) определим как полином степени m вида: Надо найти такие значения параметров, при которых квадратичный
- 7. или Необходимые условия минимума критерия R имеют вид:
- 8. Полученную линейную относительно искомых параметров a0,a1,a2, систему уравнений запишем в матричном виде: где Для удобства формирования
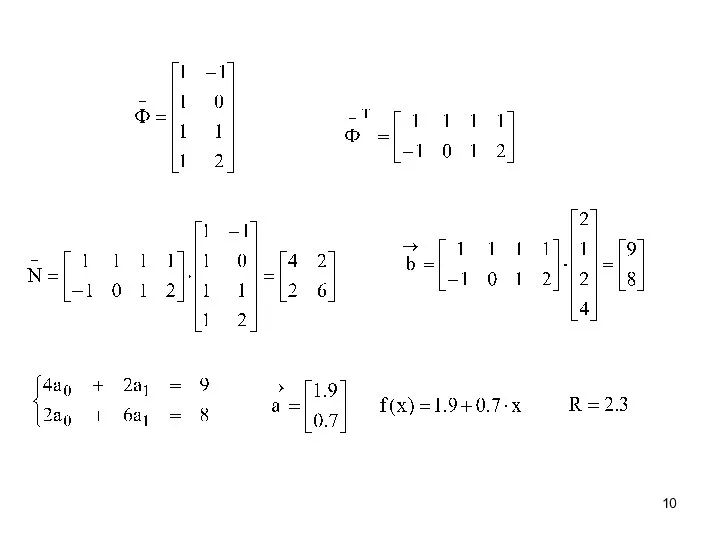
- 9. При аппроксимации полиномами высших порядков матрица будет иметь вид: Пример. Определить параметры зависимости вида используя метод
- 13. Скачать презентацию




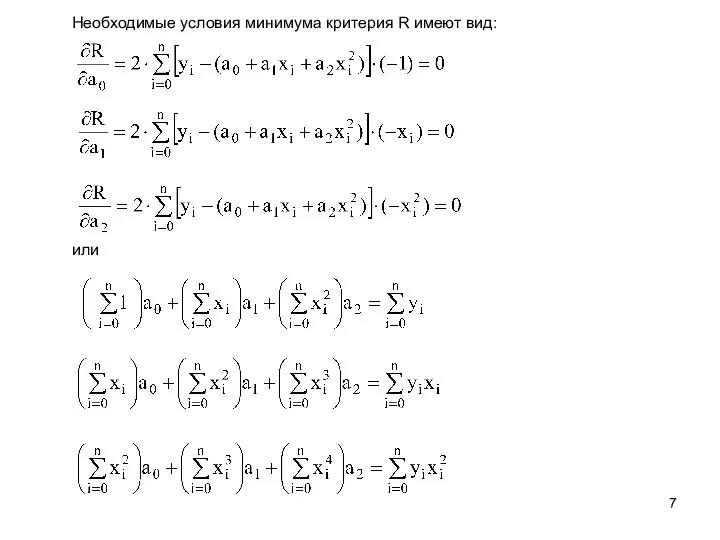



 Физиология крови
Физиология крови Виды капитального ремонта
Виды капитального ремонта Вступ. Культура як суспільне явище
Вступ. Культура як суспільне явище Спартак Москва
Спартак Москва SCAT Әуе компаниясы
SCAT Әуе компаниясы Я приглашаю вас в мир туризма
Я приглашаю вас в мир туризма Икона «Спас на Престоле». Симон Ушаков, 1670 год.
Икона «Спас на Престоле». Симон Ушаков, 1670 год. Христианское богослужение - основные понятия
Христианское богослужение - основные понятия Презентация по экономике на тему: «Деньги. История возникновения денег». Подготовили ученицы 11 «В» класса
Презентация по экономике на тему: «Деньги. История возникновения денег». Подготовили ученицы 11 «В» класса  Презентация Функции и механизм государства
Презентация Функции и механизм государства Вероучение и культ буддизма
Вероучение и культ буддизма буква д - презентация для начальной школы
буква д - презентация для начальной школы Обыкновенное чудо – люди России
Обыкновенное чудо – люди России Диссертационное исследование требования 7
Диссертационное исследование требования 7 Стильно быть стильным
Стильно быть стильным Презентация Ландшафтный дизайн
Презентация Ландшафтный дизайн  Причинение тяжкого и средней тяжести вреда здоровью Подготовили студентки ФТД-4 Группы Т-094 Зайцева Виктория, Шевченко Наталья.
Причинение тяжкого и средней тяжести вреда здоровью Подготовили студентки ФТД-4 Группы Т-094 Зайцева Виктория, Шевченко Наталья. Техногенные опасности
Техногенные опасности  Оценка качества
Оценка качества Конституционное право
Конституционное право Русская изба. Быт русских людей
Русская изба. Быт русских людей презентация к проекту Животные на войне Ермаковская школа
презентация к проекту Животные на войне Ермаковская школа Колнструктивные мероприятия и оценка обеспеченности пассивной безопасности дороги
Колнструктивные мероприятия и оценка обеспеченности пассивной безопасности дороги Христос - наша праведность (оправдание) и наше освящение
Христос - наша праведность (оправдание) и наше освящение Основы менеджмента © Бараусова Елена Александровна
Основы менеджмента © Бараусова Елена Александровна  Наше наследие
Наше наследие Возможности ТВ-приставки на платформе Ericsson (Huawei DN300)
Возможности ТВ-приставки на платформе Ericsson (Huawei DN300) Семинар-практикум (фрагмент конспекта) Бизнес-процессы в банке: описание, оптимизация, регламентация и управление Автор и ве
Семинар-практикум (фрагмент конспекта) Бизнес-процессы в банке: описание, оптимизация, регламентация и управление Автор и ве