Содержание
- 2. Вычисление пределов с помощью формулы Тейлора. Рассмотрим сначала случай неопределенности вида Пусть требуется найти предел где
- 3. Часто бывает удобно для разложений функций f(x) и g(x) использовать готовый набор разложений элементарных функций по
- 4. Случай x → ∞ сводится заменой переменной x = 1/t к случаю t → 0. ПРИМЕР
- 5. При раскрытии данным методом неопределенностей вида ∞/∞, 0·∞ и ∞ – ∞ их следует преобразовать к
- 6. Приложения формулы Тейлора к исследованию поведения функции в окрестности точки. В качестве примера применения формулы Тейлора
- 7. Доказательство. Формула Тейлора n-ого порядка для функции f(x) в данном случае имеет вид: f(x) = f(x0)
- 8. ПРИМЕР. Исследуем поведение функции в окрестности точки x0 = 0. Согласно третьему достаточному условию экстремума, точка
- 9. Родился в Париже в богатой и знатной семье. Носил звание маркиза (де Сен-Мэм) и графа (Антрмон).
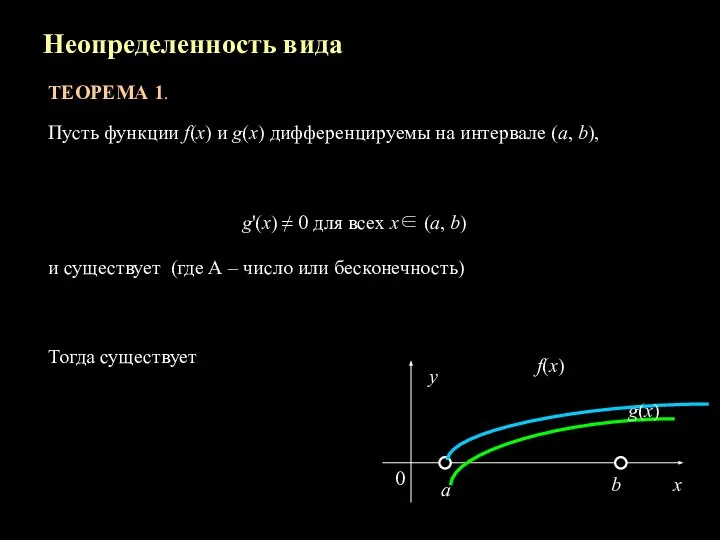
- 10. Неопределенность вида ТЕОРЕМА 1. Пусть функции f(x) и g(x) дифференцируемы на интервале (a, b), g'(x) ≠
- 11. Доказательство. Пусть х∈ (a, b). Доопределим функции f(x) и g(x) в точке а, положив f(а) =
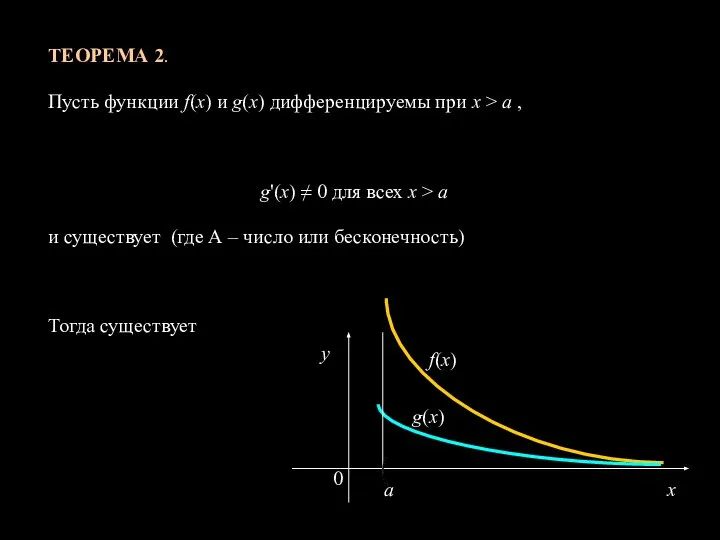
- 12. ТЕОРЕМА 2. Пусть функции f(x) и g(x) дифференцируемы при х > а , g'(x) ≠ 0
- 13. Доказательство. Можно считать, что a > 0. Положим x = 1/t. Эта функция отображает интервал (а,
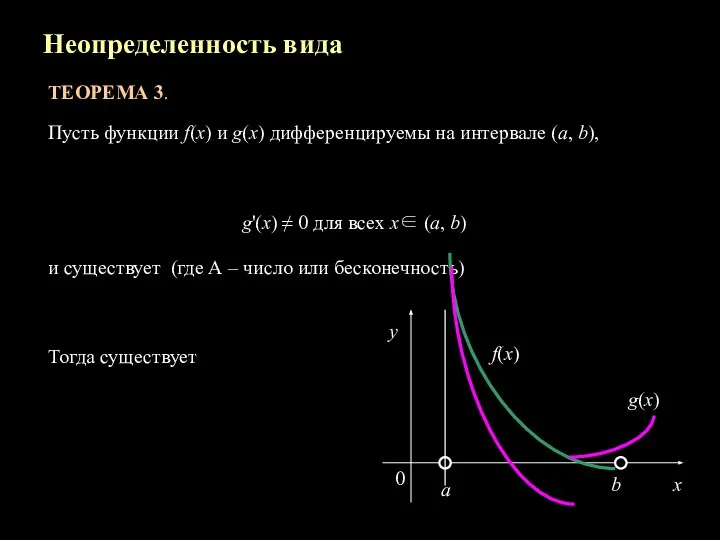
- 14. Неопределенность вида ТЕОРЕМА 3. Пусть функции f(x) и g(x) дифференцируемы на интервале (a, b), g'(x) ≠
- 15. ЗАМЕЧАНИЕ 2. Правило Лопиталя справедливо также в случае неопределенности при х → а – 0, при
- 16. Примеры. 1. 2. 3. 4.
- 17. 5. Найдем Пусть k = [α]+1. Тогда α – k 6. Найдем Пусть lnx = t.
- 19. Скачать презентацию











![5. Найдем Пусть k = [α]+1. Тогда α – k 6.](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1296490/slide-16.jpg)
 РЕКЛАМНОЕ ТВОРЧЕСТВО как искусство САМООГРАНИЧЕНИЙ
РЕКЛАМНОЕ ТВОРЧЕСТВО как искусство САМООГРАНИЧЕНИЙ Java.SE.07 Multithreading
Java.SE.07 Multithreading Птицы и человек - презентация для начальной школы_
Птицы и человек - презентация для начальной школы_ Плоскость
Плоскость «Понятие, содержание и особенности гражданской правосубъектности публично-правовых образований». Выполнили: Студентки 2 кур
«Понятие, содержание и особенности гражданской правосубъектности публично-правовых образований». Выполнили: Студентки 2 кур Нефрит - производитель одноразовой продукции для медицинских учреждений, салонов красоты, студий загара, SPA-салонов
Нефрит - производитель одноразовой продукции для медицинских учреждений, салонов красоты, студий загара, SPA-салонов Елка в Сокольниках - презентация для начальной школы
Елка в Сокольниках - презентация для начальной школы Векторное поле
Векторное поле Паломнический центр «Знаменский скит». Паломническо-туристические маршруты
Паломнический центр «Знаменский скит». Паломническо-туристические маршруты неонатальная герптеическая инфекция Студент 8 десятка,203 группы Ходакевич В. Н.
неонатальная герптеическая инфекция Студент 8 десятка,203 группы Ходакевич В. Н. История возникновения и развития международного права. (Лекция 1)
История возникновения и развития международного права. (Лекция 1) Тема лекции: Морфофункциональная классификация сердечно-сосудистой системы. Параметры гемодинамики. План: 1. Морфофункциональна
Тема лекции: Морфофункциональная классификация сердечно-сосудистой системы. Параметры гемодинамики. План: 1. Морфофункциональна Наибольший общий делитель. Наименьшее общее кратное на языке С++
Наибольший общий делитель. Наименьшее общее кратное на языке С++ Дискретные сигналы в инфотелекоммуникации (Общая теория связи, Лекция № 5)
Дискретные сигналы в инфотелекоммуникации (Общая теория связи, Лекция № 5) Оболочки головного мозга
Оболочки головного мозга  Электрическое оборудование вагонов 81-740/741 и 81-760/761. Альбом электрических схем
Электрическое оборудование вагонов 81-740/741 и 81-760/761. Альбом электрических схем Изучение массивов. (Лабораторная работа 7)
Изучение массивов. (Лабораторная работа 7) Международный день родного языка
Международный день родного языка Из опыта работы по организации дошкольной подготовки Автор: Николаева Марина Николаевна учитель начальных классов МОУ «Ново
Из опыта работы по организации дошкольной подготовки Автор: Николаева Марина Николаевна учитель начальных классов МОУ «Ново Дінамичні бібліотеки в ОС Windows Операційні системи
Дінамичні бібліотеки в ОС Windows Операційні системи Introduce to Petri nets
Introduce to Petri nets Основы семейного права. Тема 9
Основы семейного права. Тема 9 Трансформаторлар. Топтарға
Трансформаторлар. Топтарға Язык программирования JavaScript
Язык программирования JavaScript Понятие преступления. Состав преступления. Тема 2
Понятие преступления. Состав преступления. Тема 2 Проектирование электрического освещения. Лекция №2
Проектирование электрического освещения. Лекция №2 УМК «Дети-читатели» 2 класс. - презентация
УМК «Дети-читатели» 2 класс. - презентация Система технического обслуживания и ремонта вагонов
Система технического обслуживания и ремонта вагонов