Содержание
- 2. Направление выпуклости графика функции. Пусть функция f(x) дифференцируема в любой точке интервала (а,b). Тогда существует касательная
- 3. ТЕОРЕМА. Если функции f(x) имеет на интервале (а, b) вторую производную и f ´´(x) ≤ 0
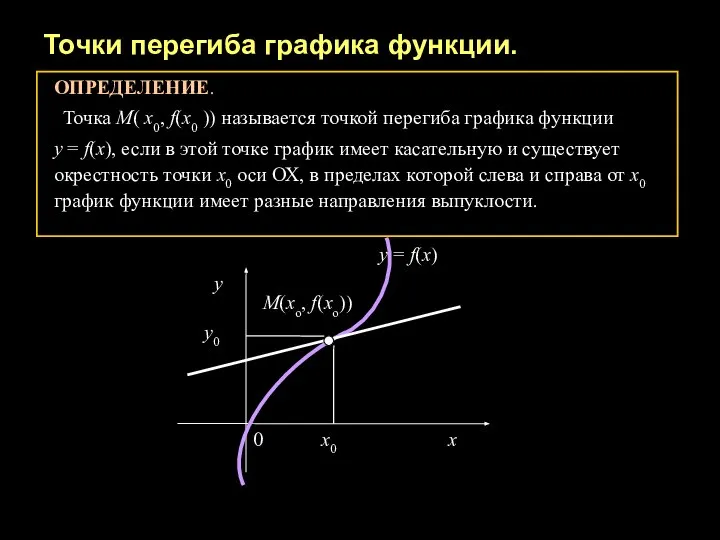
- 4. Точки перегиба графика функции. ОПРЕДЕЛЕНИЕ. Точка М( х0, f(х0 )) называется точкой перегиба графика функции у
- 5. ТЕОРЕМА (необходимое условие перегиба графика функции, имеющей непрерывную вторую производную). Если М(x0, f(x0)) точка перегиба графика
- 6. Достаточные условия перегиба. ТЕОРЕМА 1. Пусть у = f(x) непрерывна в точке x0, дважды дифференцируема в
- 7. ТЕОРЕМА 2. Если f ´´(x0) = 0, а f (3)( x0) ≠ 0, то x0 –
- 8. ПРИМЕР. Найдем направления выпуклости и точки перегиба графика функции Вычислим производные первого и второго порядка: Здесь
- 9. Общая схема построения графика функции. Изучение заданной функции f(x) и построение ее графика целесообразно проводить в
- 10. ПРИМЕР. Провести полное исследование функции и построить ее график. Область определения функции D(f) = (–∞, –1)
- 11. Найдем асимптоты графика функции, вычислив необходимые пределы. В результате получим: х = – 1 – вертикальная
- 12. Вычислим первую производную функции Найдем критические точки производной и отметим их на числовой прямой. Расставим знаки
- 13. Найдем вторую производную функции Отметим на числовой прямой критические точки второй производной. Расставим знаки второй производной
- 16. Скачать презентацию












 Закон результата Выполнила студентка 2-го курса экономического факультета Русакова Ксения
Закон результата Выполнила студентка 2-го курса экономического факультета Русакова Ксения  Puti_i_metody_poznania_istorii
Puti_i_metody_poznania_istorii Привлечение клиентов в салон красоты через Интернет
Привлечение клиентов в салон красоты через Интернет Рекурсия
Рекурсия Как создать свой сайт
Как создать свой сайт Теория и методология политической науки
Теория и методология политической науки Отчёт о прохождении производственной практики в строительной компании ООО «СК УРАЛПОЛ»
Отчёт о прохождении производственной практики в строительной компании ООО «СК УРАЛПОЛ» Бабочка Урок художественного труда 2 класс
Бабочка Урок художественного труда 2 класс Анализ причин врожденного сифилиса в Смоленской области
Анализ причин врожденного сифилиса в Смоленской области Бюджет домохозяйства
Бюджет домохозяйства GPS подтверждение доставки 2.0 (для транспортной компании)
GPS подтверждение доставки 2.0 (для транспортной компании) Циклический алгоритм. Цикл с повторителем и вложенный цикл. Урок 5
Циклический алгоритм. Цикл с повторителем и вложенный цикл. Урок 5 Маленькие хитрости большого бизнеса (1). Система мотивации сотрудников в компании IKEA
Маленькие хитрости большого бизнеса (1). Система мотивации сотрудников в компании IKEA Сочинение по картине С.Григорьева «Вратарь» Р – 7 класс
Сочинение по картине С.Григорьева «Вратарь» Р – 7 класс Понятие о профилактике зависимости от ПАВ
Понятие о профилактике зависимости от ПАВ Двухстековая схема IPv4-IPv6
Двухстековая схема IPv4-IPv6 Культурно-массовое мероприятие
Культурно-массовое мероприятие ЛЕКЦИЯ Глобализация как современная тенденция развития мирового хозяйства. Измерение глобальной и региональной торговой интег
ЛЕКЦИЯ Глобализация как современная тенденция развития мирового хозяйства. Измерение глобальной и региональной торговой интег Электронные навигаторы успеха в учении (из опыта работы ГБОУ города Москвы СОШ с углубленным изучением экологии №446) Иванов
Электронные навигаторы успеха в учении (из опыта работы ГБОУ города Москвы СОШ с углубленным изучением экологии №446) Иванов Демократія. Ознаки демократії
Демократія. Ознаки демократії Улучшение визуализации. Настройка монитора
Улучшение визуализации. Настройка монитора Wonders of the World
Wonders of the World Система права и система законодательства
Система права и система законодательства Локальные компьютерные сети
Локальные компьютерные сети Знакомство с языком HTML
Знакомство с языком HTML Политика и религия
Политика и религия Қожа Ахмет Иассауи
Қожа Ахмет Иассауи Презентация Полимеры и пластмассы
Презентация Полимеры и пластмассы