Содержание
- 2. Теория нечетких множеств раздел прикладной математики, посвященный методам анализа неопределенных данных, в которых описание неопределенностей реальных
- 3. Нечеткое управление одна из самых результативных областей применения теории нечетких множеств
- 4. Области использования приложений с нечеткой логикой в Internet: диагностика и восстановление сетевых конфигураций и управление производственными
- 5. Информация о системе носит субъективный характер и ее представление в естественном языке содержит большое число неопределенностей
- 6. Fuzzy sets Л. Заде Нечеткое множество - это математическая модель класса с нечеткими, или размытыми границами
- 7. Нечеткое множество Совокупность элементов, обладающих некоторым общим свойством, но … в разной степени
- 8. Нечеткое множество А в Х совокупность пар вида (x, μA(x)), где x∈X, μА : x→ [0,1]
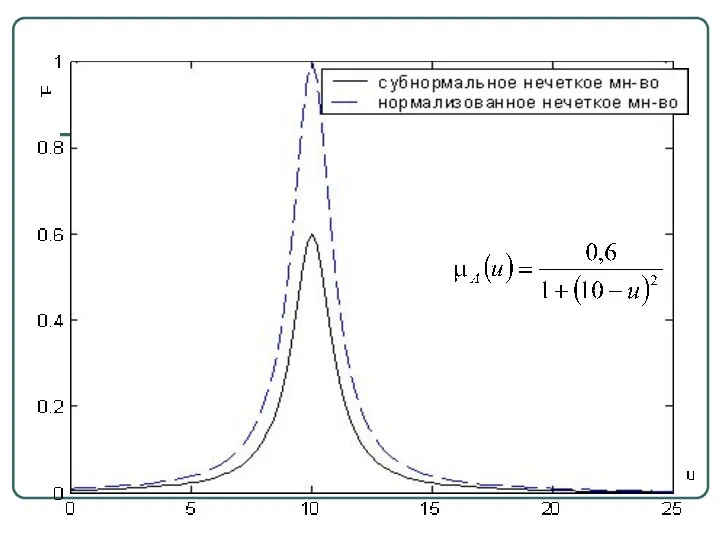
- 10. Определения supμА(x) называется высотой нечеткого множества A Нечеткое множество A нормально, если его высота равна 1,
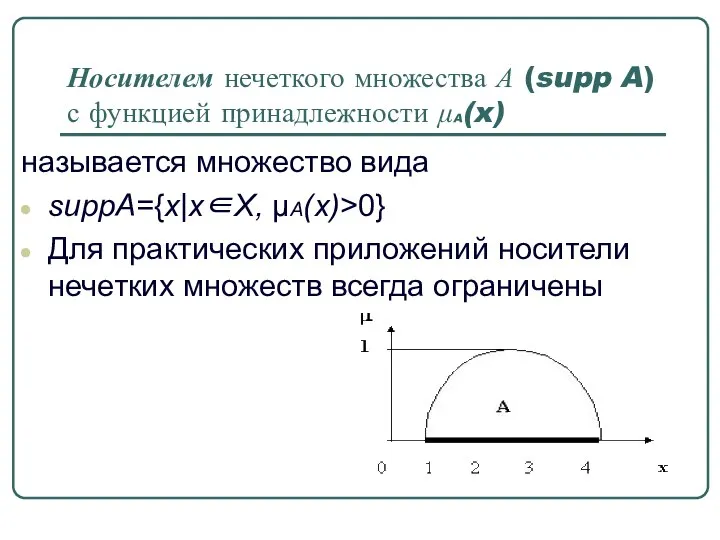
- 11. Носителем нечеткого множества А (supp A) с функцией принадлежности μA(x) называется множество вида suppA={x|x∈X, μA(x)>0} Для
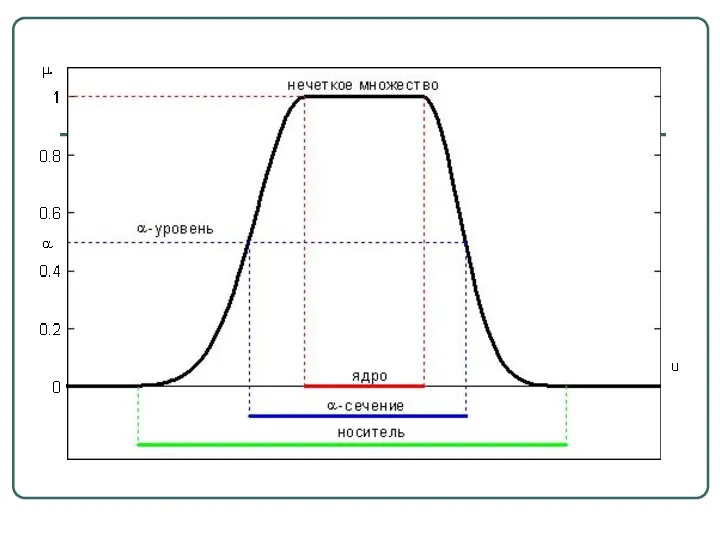
- 12. Ядром нечеткого множества называется четкое подмножество универсального множества U, элементы которого имеют степени принадлежности, равные единице
- 13. α-сечением (или множеством α-уровня) нечеткого множества называется четкое подмножество универсального множества U, элементы которого имеют степени
- 15. Операции над нечеткими множествами нечеткие множества А и В равны, если μA(x)=μВ(x); нечеткое множество С является
- 17. Пример 1. suppA = { x| величина x близка к 1}, suppB = {x| величина x
- 18. Примеры записи нечеткого множества Пусть Х = {x1, x2, x3, x4, x5 }, M = [0,1];
- 19. A = {0,3/x1; 0/x2; 1/x3; 0,5/x4; 0,9/x5 }, или A = 0,3/x1 + 0/x2 + 1/x3
- 20. Лингвистические переменные (linguistic variable) Терм–множеством (term set) называется множество всех возможных значений лингвистической переменной. Термом (term)
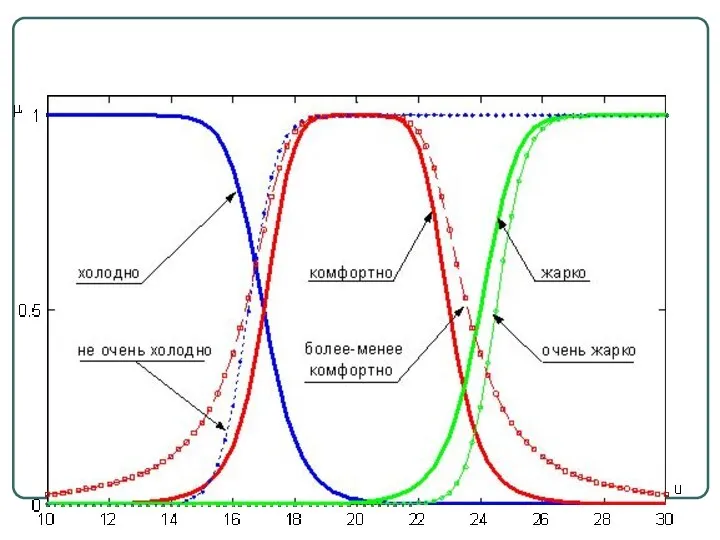
- 21. Лингвистическая переменная Х = "температура в комнате" универсальное множество U=[5; 35] ; терм-множество T={"холодно", "комфортно", "жарко"}
- 23. Пример нечеткого множества Пусть Х= {0,1,2,..,10}, M =[0,1]. Нечеткое множество "несколько" можно определить следующим образом: "несколько"={0,5/3+0,8/4+1/5+1/6+0,8/7+0,5/8}
- 24. Построение функций принадлежности нечетких множеств прямые и косвенные методы прямые методы используются для измеримых понятий, таких
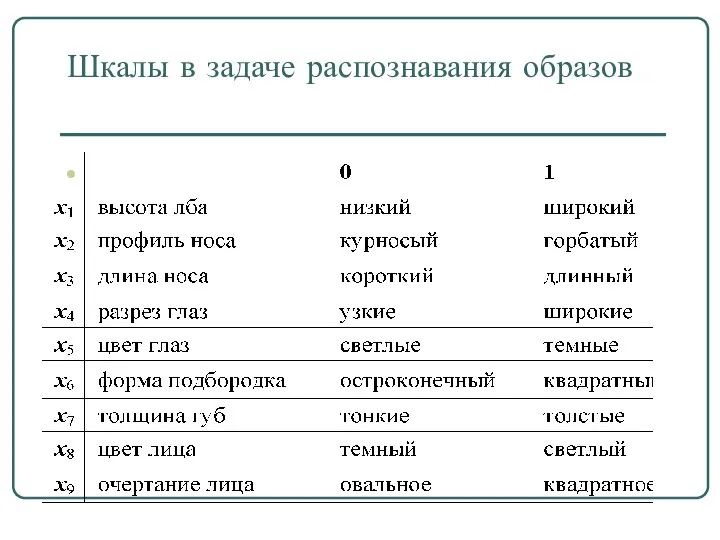
- 25. Шкалы в задаче распознавания образов
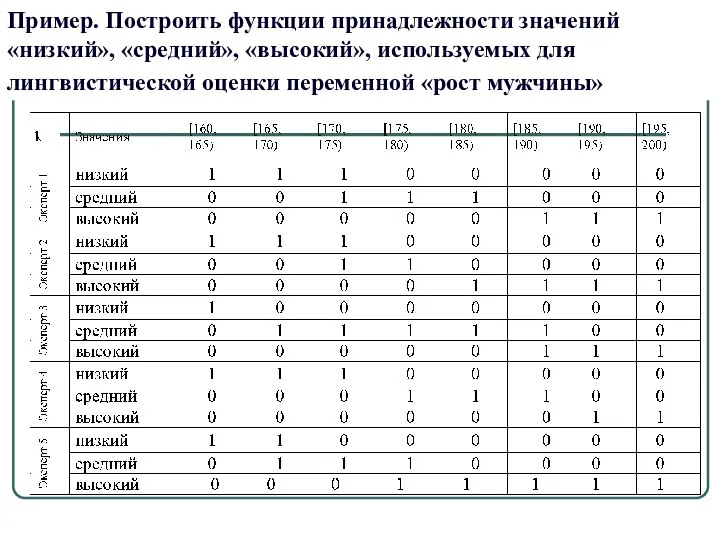
- 26. Пример. Построить функции принадлежности значений «низкий», «средний», «высокий», используемых для лингвистической оценки переменной «рост мужчины»
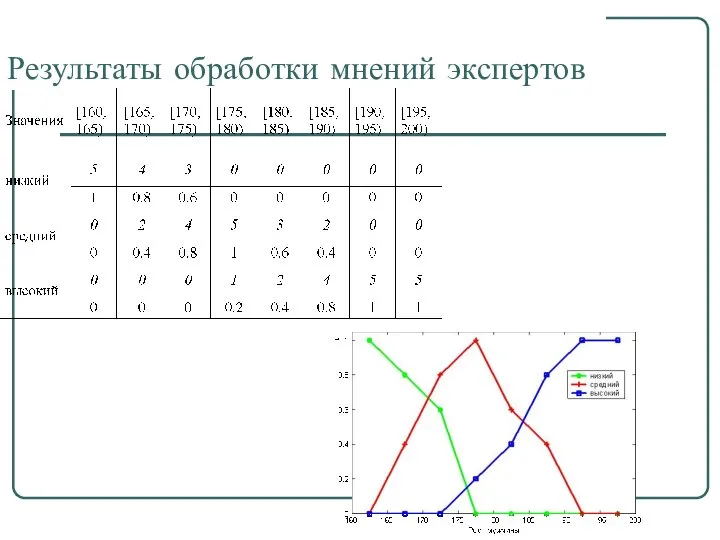
- 27. Результаты обработки мнений экспертов
- 28. Преобразования нечеткого множества Дефаззификацией (defuzzification) называется процедура преобразования нечеткого множества в четкое число
- 29. Для многоэкстремальных функций принадлежности в Fuzzy Logic Toolbox запрограммированы методы дефаззификации: Centroid - центр тяжести; Bisector
- 30. Процедура дефаззификации аналогична нахождению характеристик положения (математического ожидания, моды, медианы) случайных величин в теории вероятности Простейшим
- 31. Метод центра тяжести Дефаззификация нечеткого множества по методу центра тяжести осуществляется по формуле
- 32. Физическим аналогом является нахождение центра тяжести плоской фигуры, ограниченной осями координат и графиком функции принадлежности нечеткого
- 33. Для дискретного универсального множества дефаззификация нечеткого множества по методу центра тяжести осуществляется по формуле
- 34. Метод медианы Дефаззификация нечеткого множества по методу медианы состоит в нахождении такого числа a, что
- 35. Геометрическая интерпретация метода медианы нахождение такой точки на оси абцисс, что перпендикуляр, восстановленный в этой точке,
- 36. Для дискретного универсального множества дефаззификация нечеткого множества по методу медианы осуществляется по формуле
- 37. Метод центра максимумов Дефаззификация нечеткого множества по методу центра максимумов осуществляется по формуле где G –
- 38. В методе центра максимумов находится среднее арифметическое элементов универсального множества, имеющих максимальные степени принадлежностей. Если множество
- 39. В методе центра максимумов находится среднее арифметическое элементов универсального множества, имеющих максимальные степени принадлежности. Если множество
- 40. В дискретном случае дефаззификация по методам наибольшего из максимумов и наименьшего из максимумов осуществляется по формулам
- 41. Пример Провести дефаззификацию нечеткого множества «мужчина среднего роста», для которого нечеткое множество = {0/155; 0.1/160; 0.3/165;
- 42. Решение: Применяя формулу , получаем: {0/155; 0.1/160; 0.3/165; 0.8/170; 1/175; 1/180; 0.5/185; 0/190}
- 43. Задача достижения нечетко определенной цели (подход Беллмана-Заде) Пусть Х – универсальное множество альтернатив, т.е. универсальная совокупность
- 44. Нечеткая цель G Функция принадлежности нечеткой цели μG: X → [0,1]. Чем больше степень принадлежности альтернативы
- 45. Пусть некоторая альтернатива x обеспечивает достижение цели со степенью μG(x), удовлетворяет ограничениям со степенью μС(x) Решить
- 46. При наличии нескольких целей и ограничений нечеткое решение описывается функцией принадлежности μD(x)=min{μG1(x),…,μGn(x),μC1(x),…,μCn(x)}
- 47. Оптимальной в смысле подхода Беллмана-Заде будет альтернатива х*, для которой μD(x) максимальна х*: μD(x*)=max μD(x) x∈X
- 48. - коэффициент относительной важности i-ой цели, - коэффициент относительной важности j-го ограничения
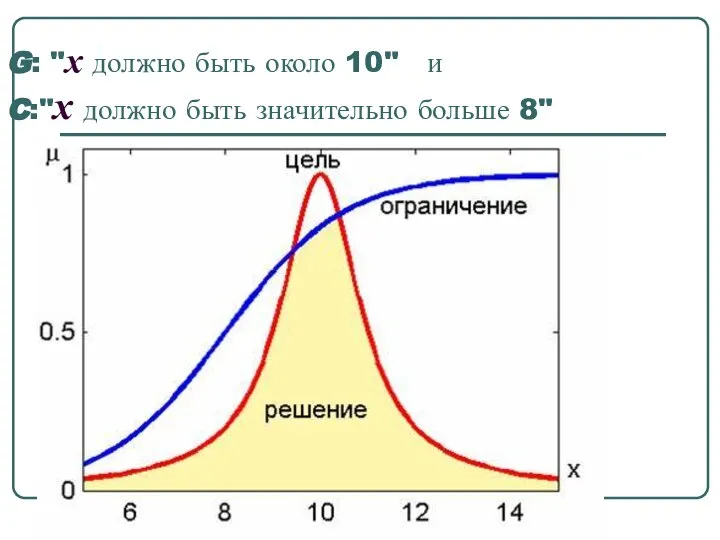
- 49. G: "x должно быть около 10" и C:"x должно быть значительно больше 8"
- 50. При принятии решения по схеме Беллмана-Заде не делается никакого различия между целью и ограничениями. Всякое разделение
- 52. Скачать презентацию















![Лингвистическая переменная Х = "температура в комнате" универсальное множество U=[5; 35] ; терм-множество T={"холодно", "комфортно", "жарко"}](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1299111/slide-20.jpg)
![Пример нечеткого множества Пусть Х= {0,1,2,..,10}, M =[0,1]. Нечеткое множество "несколько"](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1299111/slide-22.jpg)

















![Нечеткая цель G Функция принадлежности нечеткой цели μG: X → [0,1].](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1299111/slide-43.jpg)





 Изображение пространства. Урок ИЗО
Изображение пространства. Урок ИЗО Генераторы электрических сигналов
Генераторы электрических сигналов Ключи к успеху
Ключи к успеху Презентация Определение цели и задачи научного исследования
Презентация Определение цели и задачи научного исследования Текстура. Характеристики текстуры
Текстура. Характеристики текстуры Технологический процесс смесеприготовления
Технологический процесс смесеприготовления 1.04.2010 Удивительные квадратные уравнения Мне приходится делить свое время между политикой и уравнениями. Однако уравнения, по-моем
1.04.2010 Удивительные квадратные уравнения Мне приходится делить свое время между политикой и уравнениями. Однако уравнения, по-моем Алгоритмизация и программирование. Язык C. Целочисленные алгоритмы (§ 38 - § 45)
Алгоритмизация и программирование. Язык C. Целочисленные алгоритмы (§ 38 - § 45) Почему бухгалтерия должна быть похожа на Вконтакте?
Почему бухгалтерия должна быть похожа на Вконтакте? Презентация Примеры использования различных моделей деятельности по связям с общественностью за рубежом
Презентация Примеры использования различных моделей деятельности по связям с общественностью за рубежом Переломы костей
Переломы костей  Петербургский музей кукол
Петербургский музей кукол Дизайн и архитектура сада
Дизайн и архитектура сада Die Feste
Die Feste Конституция Российской Федерации о правах ребенка
Конституция Российской Федерации о правах ребенка Презентация Женское легкое платье
Презентация Женское легкое платье Презентация "В ней есть душа, в ней есть свобода (Времена года в русском искусстве)" - скачать презентации по МХК
Презентация "В ней есть душа, в ней есть свобода (Времена года в русском искусстве)" - скачать презентации по МХК Презентация Спрос, предложение и рыночное равновесие
Презентация Спрос, предложение и рыночное равновесие Презентация Региональные таможенные управления РФ (РТУ РФ)
Презентация Региональные таможенные управления РФ (РТУ РФ)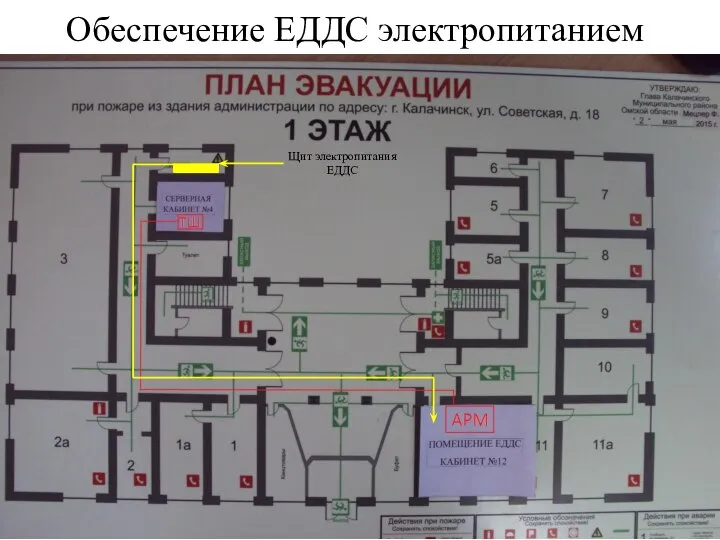 Обеспечение ЕДДС электропитанием
Обеспечение ЕДДС электропитанием Водородоподобный атом. Уровни энергии
Водородоподобный атом. Уровни энергии  Буддизм как явление духовной культуры
Буддизм как явление духовной культуры Системы управления качеством. Лекция 3
Системы управления качеством. Лекция 3 Землетрясения
Землетрясения  Основные понятия и положения МКТ
Основные понятия и положения МКТ Eager loading c#
Eager loading c# Модернизация 3d Принтера picasso designer pro 250
Модернизация 3d Принтера picasso designer pro 250 «Что такое экономика» Цель урока изучить основные понятия: материальное и нематериально производство, общественные и личные потребности, производственные потребности, предмет труда, средства труда, совокупный общественный продукт, труд, факторы
«Что такое экономика» Цель урока изучить основные понятия: материальное и нематериально производство, общественные и личные потребности, производственные потребности, предмет труда, средства труда, совокупный общественный продукт, труд, факторы