Производная Производной функции f в точке х0 называется число, к которому стремится разностное отношение при Δх, стремящемся
Содержание
- 2. Правила дифференцирования
- 3. Пример
- 4. Производная сложной функции
- 5. Пример
- 6. Производная тригонометрических функций
- 7. Пример
- 8. Метод интервалов
- 9. Пример
- 10. Возрастание (убывание) функции Найти промежутки возрастания и убывания функции:
- 11. Пример
- 12. Внутренние точки области определения функции, в которых ее производная равна нулю или не существует, называются критическими
- 13. Признак максимума функции Если в точке х0 производная меняет знак с плюса на минус, то х0
- 14. Признак минимума функции Если в точке х0 производная меняет знак с минуса на плюса, то х0
- 15. Пример Исследовать на экстремумы функцию
- 16. Решение х=2 (меняет знак с плюса на минус) – точка максимума х= 3 (меняет знак с
- 17. Исследование функций и построение их графиков
- 18. Схема исследования функции (10 класс) Найти область определения и значения данной функции Выяснить, обладает ли функция
- 19. Исследовать функцию и построить ее график:
- 20. Решение Область определения: D (y) = R Четность, нечетность, периодичность тогда функция является ни четной ни
- 21. 3. Найдем точки пересечения графика с Ох (у = 0):
- 22. Пересечения с Оу: х = 0, у = 0 Возьмем также дополнительные точки: 4. Найдем производную:
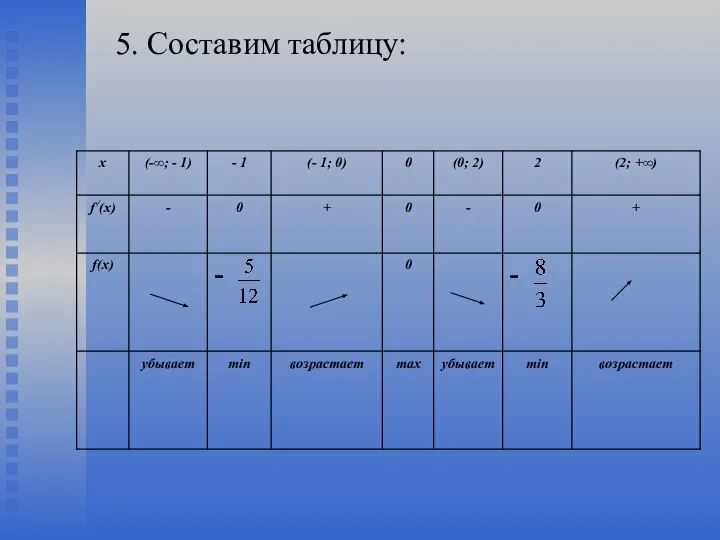
- 23. 5. Составим таблицу:
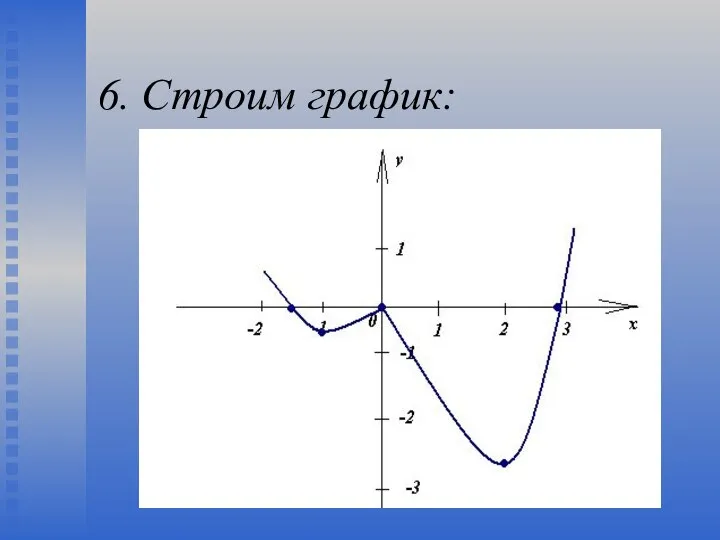
- 24. 6. Строим график:
- 25. Наибольшее и наименьшее значение функции Чтобы найти наибольшее и наименьшее значения функции, имеющей на отрезке конечное
- 26. Пример Найдем наибольшее и наименьшее значения функции на отрезке
- 27. Определение первообразной. Основное свойство первообразной
- 28. Функция F называется первообразной для функции f на заданном промежутке, если для всех х из этого
- 29. Пример № 1 Функция есть первообразная для функции на интервале (- ∞;∞), т.к.
- 30. Пример № 2
- 31. Решить
- 32. Теорема Любая первообразная для функции f на промежутке I может быть записана в виде F(x) +
- 33. Таблица первообразных
- 34. Правило № 1 Если F есть первообразная для f, а G – первообразная для g, то
- 35. Пример Найти общий вид первообразных для функции
- 36. Правило № 2 Если F есть первообразная для f, а k- постоянная, то функция kF –
- 37. Пример Найдем одну из первообразных для функции
- 38. Правило № 3 Если F(х) есть первообразная для f(x), а k и b – постоянные, причем
- 39. Пример Найдем одну из первообразных для функции
- 40. Решить
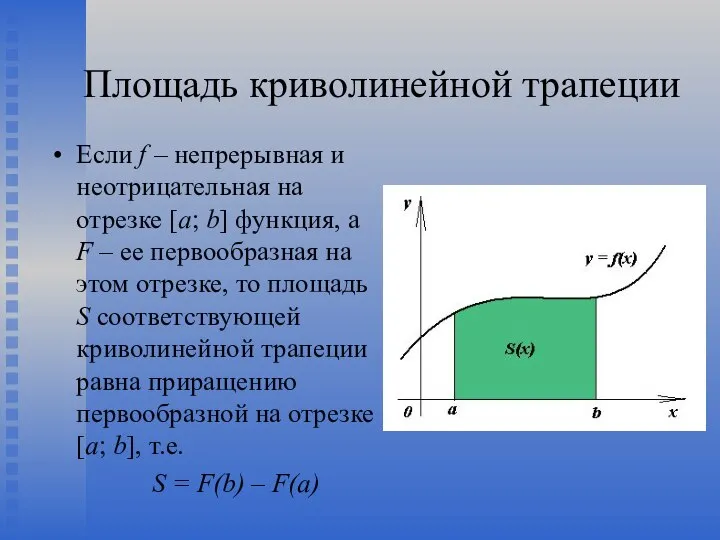
- 41. Площадь криволинейной трапеции Если f – непрерывная и неотрицательная на отрезке [a; b] функция, а F
- 42. Пример Вычислим площадь S криволинейной трапеции, ограниченной графиком функции , прямыми у = 0, х =
- 43. Понятие об интеграле Для любой непрерывной на отрезке [a; b] функции f (не обязательно неотрицательной) Sn
- 44. Читается: «Интеграл от a до b эф от икс дэ икс» Числа a и b –
- 45. Формула Ньютона - Лейбница Если F – первообразная для f на [a; b], то
- 47. Скачать презентацию





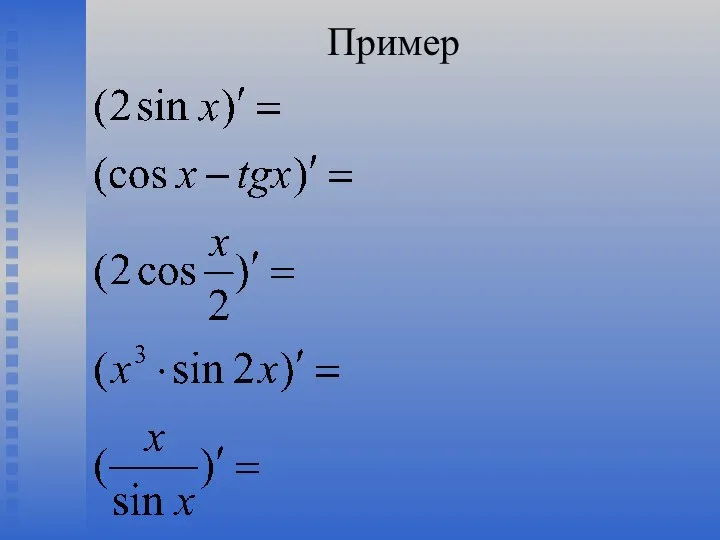





















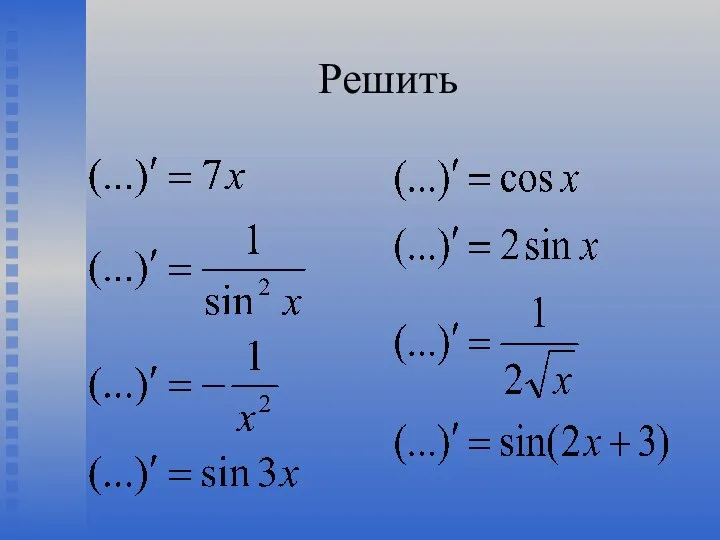










![Понятие об интеграле Для любой непрерывной на отрезке [a; b] функции](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1257969/slide-42.jpg)

![Формула Ньютона - Лейбница Если F – первообразная для f на [a; b], то](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1257969/slide-44.jpg)
 Вишивка - душа української оселі
Вишивка - душа української оселі Значение государственной службы в Российской Федерации
Значение государственной службы в Российской Федерации Программа дополнительного образования «Скалолазание»
Программа дополнительного образования «Скалолазание» АНТИЧНАЯ СКУЛЬПТУРА
АНТИЧНАЯ СКУЛЬПТУРА  James Fenimore Cooper
James Fenimore Cooper Małgorzata Alacoque
Małgorzata Alacoque Морфобиологическая характеристика и продуктивность сорго-суданковых гибридов в предгорной зоне Республики Крым
Морфобиологическая характеристика и продуктивность сорго-суданковых гибридов в предгорной зоне Республики Крым Основы программирования. Указатели и динамические массивы
Основы программирования. Указатели и динамические массивы Откуда берутся снег и лед ? - презентация для начальной школы_
Откуда берутся снег и лед ? - презентация для начальной школы_ Влияние обработки борами различной абразивности на адгезию композитов к твердым тканям зуба Научный руководитель: Позовская Е.В.
Влияние обработки борами различной абразивности на адгезию композитов к твердым тканям зуба Научный руководитель: Позовская Е.В. Комплексированный моноимпульсный вторичный радиолокатор (МВРЛ-К) «Лира-ВМ»
Комплексированный моноимпульсный вторичный радиолокатор (МВРЛ-К) «Лира-ВМ» Вентиляция. Классификация систем вентиляции. Оборудование для вентиляции
Вентиляция. Классификация систем вентиляции. Оборудование для вентиляции «Організація життєдіяльності учнівського та педагогічного колективів через управління НВП на засадах компетентнісно – зоріє
«Організація життєдіяльності учнівського та педагогічного колективів через управління НВП на засадах компетентнісно – зоріє «Моя профессиональная траектория» Человек выбирает дело или дело выбирает человека?
«Моя профессиональная траектория» Человек выбирает дело или дело выбирает человека? Основы безопасности жизнедеятельности 11 класс Авторы – А.Т. Смирнов, Б.О. Хренников Презентация учителя ОБЖ МОУ Школы №25 г.о. Сама
Основы безопасности жизнедеятельности 11 класс Авторы – А.Т. Смирнов, Б.О. Хренников Презентация учителя ОБЖ МОУ Школы №25 г.о. Сама класс Общественные движения 50-80-гг 19 века 1
класс Общественные движения 50-80-гг 19 века 1 Аукцион знаний ТИТАНЫ ВОЗРОЖДЕНИЯ.
Аукцион знаний ТИТАНЫ ВОЗРОЖДЕНИЯ. Rezultaty_fokus-grupp_po_Ot_i_PB_SRS
Rezultaty_fokus-grupp_po_Ot_i_PB_SRS Модульное тестирование ( unit testing)
Модульное тестирование ( unit testing) Метод Мерцалова
Метод Мерцалова Багатопотоковість і синхронізація. (Лекція 10)
Багатопотоковість і синхронізація. (Лекція 10) Разминка . История отечественного государства и права. Выполнила: Простакова Вероника студентка 1 курса группа Ю-123Б
Разминка . История отечественного государства и права. Выполнила: Простакова Вероника студентка 1 курса группа Ю-123Б 425266.ppt
425266.ppt Обучение граждан предпенсионного возраста
Обучение граждан предпенсионного возраста Моя продукция faberlic
Моя продукция faberlic Организация и расчет затрат на проведение модернизации шестеренной клети с целью увеличения срока службы
Организация и расчет затрат на проведение модернизации шестеренной клети с целью увеличения срока службы Проектирование высоконагруженных систем. Лекция №1
Проектирование высоконагруженных систем. Лекция №1 Ахатова Альбина Хамитовна
Ахатова Альбина Хамитовна